Problem P. 5640. (March 2025)

P. 5640. In Las Palmas, the largest city in the Canary Islands, there is a unique exhibition in Europe that shows the world's aquatic life. One of the attractions of the exhibition is a 400 cubic metre vertical cylindrical marine aquarium, which is serviced by divers. Looking horizontally around the aquarium, how much of the aquarium wall is visible to a diver at a distance \(\displaystyle d\) from the axis of symmetry of the cylinder of radius \(\displaystyle R\)? The refractive index of the water is \(\displaystyle n\).

(5 pont)

Deadline expired on April 15, 2025.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Az alábbi felülnézeti ábrán az akváriumot az \(\displaystyle O_1\) középpontú \(\displaystyle k_1\) kör szemlélteti, a búvár helyzetét pedig a \(\displaystyle B\) pont. Mivel a fény útja megfordítható, a kérdést feltehetjük így is: a \(\displaystyle B\) pontból vízszintesen kiinduló fénysugarak a \(\displaystyle k_1\) kör mely részén tudnak kilépni az akváriumból?

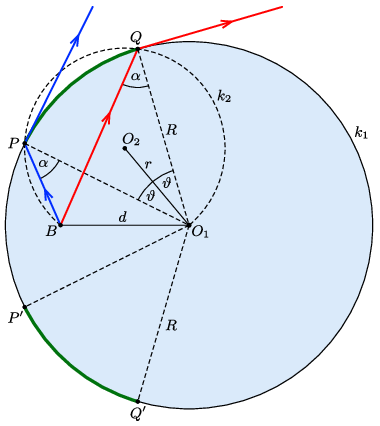
Egy fénysugár kilépésének feltétele, hogy a beesési szög kisebb legyen a teljes visszaverődés \(\displaystyle \alpha=\arcsin(1/n)\) határszögénél. (Könnyen belátható, hogy ez akkor is igaz marad, ha az akvárium falának fénytörését is figyelembe vesszük, feltéve, hogy a falvastagság sokkal kisebb az \(\displaystyle R\) sugár értékénél.) Tekintsünk egy olyan fénysugarat, amely éppen a kritikus \(\displaystyle \alpha\) beesési szögben, valamely \(\displaystyle P\) pontban érkezik az akvárium falához (lásd a kék töröttvonalat az ábrán). A \(\displaystyle P\) pont tehát rajta van a \(\displaystyle BO_1\) szakaszhoz tartozó, \(\displaystyle \alpha\) szögű \(\displaystyle k_2\) látószögköríven; jelöljük ennek középpontját \(\displaystyle O_2\)-vel! A \(\displaystyle k_2\) körív az eredeti \(\displaystyle k_1\) kört nem csak a \(\displaystyle P\) pontban, hanem egy másik \(\displaystyle Q\) pontban is metszi, azaz létezik egy másik fénysugár is (az ábrán a piros töröttvonal), amely a teljes visszaverődés határhelyzetében halad. A \(\displaystyle k_1\) kör (rövidebb) \(\displaystyle PQ\) íve mentén az akvárium falát elérő fénysugarak mind teljes visszaverődést szenvednek, mert ezekből a pontokból nézve a \(\displaystyle BO_1\) szakasz \(\displaystyle \alpha\)-nál nagyobb szögek alatt látszik. Ugyancsak nem jut ki fény a \(\displaystyle PQ\) körív \(\displaystyle BO_1\) tengelyre való tükrözésével kapott \(\displaystyle P'Q'\) köríven sem. Ha a \(\displaystyle k_1\) kör \(\displaystyle PQ\) ívéhez tartozó középponti szöget \(\displaystyle 2\vartheta\) módon jelöljük, akkor a \(\displaystyle k_1\) kör kerületének

\(\displaystyle \eta=\frac{2\pi-4\vartheta}{2\pi}=1-\frac{2\vartheta}{\pi}\)

hányadát tudja fény elhagyni.

Hátra van még a \(\displaystyle \vartheta\) szög meghatározása. Ehhez először is vegyük észre, hogy az \(\displaystyle O_1O_2B\) háromszög egyenlőszárú, valamint a kerületi és középponti szögek tétele miatt \(\displaystyle O_1O_2B\angle=2\alpha\). Ennek segítségével a \(\displaystyle k_2\) körív sugara kiszámítható:

\(\displaystyle r=\frac{d}{2\sin\alpha}=\frac{nd}{2}.\)

Most tekintsük a szintén egyenlőszárú \(\displaystyle O_1O_2P\) háromszöget, melyben a \(\displaystyle \vartheta\) szög koszinusza így írható:

\(\displaystyle \cos\vartheta=\frac{R}{2r}=\frac{R}{nd}.\)

Mindezek felhasználásával a feladat kérdésére a válasz megadható:

\(\displaystyle \eta=1-\frac{2}{\pi}\arccos\frac{R}{nd}.\)

Ennek az eredménynek csak \(\displaystyle R/(nd)\leq 1\) esetén van értelme. Ha a búvár \(\displaystyle d\leq R/n\) távolságra van az akvárium szimmetriatengelyétől, akkor víszintesen körbenézve minden irányban kilát a tartályból, azaz \(\displaystyle \eta=1\).

Statistics:

9 students sent a solution.
5 points:	Bencze Mátyás, Fekete Lúcia, Ujvári Sarolta.
4 points:	Tóthpál-Demeter Márk.
3 points:	1 student.
2 points:	2 students.
Unfair, not evaluated:	2 solutionss.

Problems in Physics of KöMaL, March 2025