 Problem P. 5642. (March 2025)
Problem P. 5642. (March 2025)
P. 5642. As early as 1679, Newton suggested that the rotation of the Earth could be proved by a mechanical experiment such that the eastward deflection of a small ball in free fall is measured. Hooke, who was secretary of the Royal Society in Newton's time and also an excellent experimenter, made such measurements in 1680. In a sufficiently wealthy and ambitious equatorial country, the experiment, which was proposed almost 350 years ago, was to be repeated by modern equipment. The plan is to drop tiny steel balls onto a wax plate in a 200 m high vertical tube, from which air was sucked out (in a vacuum tower). Determine the magnitude of the deflection by calculating
a) in an inertial frame of reference,
b) in the coordinate system rotating (accelerating) with the Earth.
(6 pont)
Deadline expired on April 15, 2025.
Sorry, the solution is available only in Hungarian. Google translation
I. Megoldsás. a) Jelöljük a Föld sugarát \(\displaystyle R\)-rel, a szögsebességét \(\displaystyle \omega\)-val, a torony magasságát pedig \(\displaystyle h\)-val. Az esés ideje ekkor \(\displaystyle T=\sqrt{\frac{2h}{g}}\), ahol \(\displaystyle g\) a nehézségi gyorsulás nagysága az Egyenlítőnél.
Inerciarendszerből nézve a test kezdősebessége (keleti irányban)
\(\displaystyle v_0=(R+h)\omega.\)
Ha az elejtésétől számított \(\displaystyle t\) idő alatt a test elmozdulása keleti irányban \(\displaystyle x(t)\), akkor a rá ható nehézségi erő vízszintes komponense \(\displaystyle -mg\frac{x}{R}\), és így a vízszintes irányú mozgás dinamikai egyenlete:
\(\displaystyle a_x(t)=-\frac{g}{R}\cdot x(t).\)
Ez a gyorsulás onnan származik, hogy a nehézségi erőtér nem homogén, iránya nem esik egybe a kiindulási ponthoz tartozó függőlegessel. (A nehézségi erő nagyságának változását \(\displaystyle h\ll R\) miatt elhanyagolhatjuk.)
Felismerhetjük, hogy a fenti egyenlet a harmonikus rezgőmozgás mozgásegyenlete, amelynek megoldása \(\displaystyle x(0)=0\) és \(\displaystyle v_0\) kezdőfeltételek mellett
\(\displaystyle x(t)= \sqrt{\frac{R}{g}}(R+h)\omega\sin\sqrt{\frac{g}{R}}t,\)
így a teljes elmozdulás \(\displaystyle T\) idő alatt
\(\displaystyle x_\textrm{test}= \sqrt{\frac{R}{g}}(R+h)\omega\,\sin\sqrt{\frac{g}{R}}T.\)
Mivel \(\displaystyle \varphi\equiv\sqrt{\tfrac{g}{R}}T\ll 1\), alkalmazhatjuk a szinusz függvény
\(\displaystyle \sin\varphi\approx\varphi-\frac{\varphi^3}{6}\)
közelítő formuláját. (Az elsőrendű tagból származó elmozdulást éppen kiejti majd a torony aljának elmozdulása, így a keresett eltérülés a harmadrendű tagból fog származni.) Ezzel kapjuk, hogy
\(\displaystyle x_\textrm{test}\approx(R+h)\left(\omega T-\frac{g\omega T^3}{6R}\right),\)
vagyis \(\displaystyle h=gT^2/2\) felhasználásával és a legkisebb, \(\displaystyle h/R\)-rel arányos tag elhanyagolásával
\(\displaystyle x_\textrm{test}\approx R\omega T+\frac{1}{3}{g\omega T^3.}\)
A jobb oldal első tagja éppen a torony aljának elmozdulása:
\(\displaystyle R\omega T=x_\textrm{torony alja},\)
így a leejtett golyó a torony aljától
\(\displaystyle \Delta x=x_\textrm{test}-x_\textrm{torony alja}=\frac{1}{3}g\omega T^3,\)
ami a megadott toronymagasság esetén kb. 6 cm.
Megjegyzés. Ha nem vennénk figyelembe a nehézségi erő irányának kicsiny változását, akkor a hibás
\(\displaystyle \Delta x=h\omega T=\frac{1}{2}g\omega T^3\approx 9\,\mathrm{cm}\)
,,eredményt'', vagyis a helyes érték másfélszeresét kapnánk.
b) Forgó rendszerben a keleti irányba mutató Coriolis-gyorsulás: \(\displaystyle a_x=2v\omega=2gt\omega\), az ehhez tartozó sebesség: \(\displaystyle v_x=g\omega t^2\), és végül az elmozdulás: \(\displaystyle x=\tfrac{1}{3}g\omega t^3=\tfrac{1}{3}g\omega\left(\sqrt{\tfrac{2h}{g}}\right)^3=\tfrac{2}{3}\omega ht=\tfrac{2}{3}\omega h\sqrt{\tfrac{2h}{g}}\approx 6\,\mathrm{cm}\).
II. Megodás. a) A \(\displaystyle h\) magasságban (az erősen torzított ábrán a \(\displaystyle B\) pontból) elejtett test tulajdonképpen egy olyan ellipszis pályán halad, aminek az egyik fókuszpontja a Föld \(\displaystyle O\) középpontja, a nagytengely egyik végpontja pedig a \(\displaystyle B\) pont. Ez a görbe a \(\displaystyle C\) pontban metszi a földfelszínt. Az esés \(\displaystyle T=\sqrt{2h/g}\) ideje alatt az \(\displaystyle \omega\) szögsebességgel forgó felszín \(\displaystyle A\) pontja az \(\displaystyle A^{\prime}\) pontba kerül. A feladatunk az \(\displaystyle \overline{A^{\prime}C}\) szakasz \(\displaystyle \Delta x\) hosszának a meghatározása.
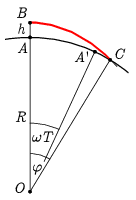
Megjegyzés. Hogy érzékeljük a nagyságrendeket: \(\displaystyle \tfrac{h}{R}\sim 3\cdot 10^{-5}\), vagy \(\displaystyle \omega T\sim\varphi\sim 5\cdot 10^{-4}\,\mathrm{rad}\). Ezeket az arányokat tükröző ábrán nyilván nem látszana semmi, ezért csak erős torzítás árán tudjuk bemutatni a részleteket.
Kepler II. törvénye értelmében az eső test úgy mozog, hogy a vezérsugár területi sebessége állandó. Ez a sebesség
\(\displaystyle (R+h)\frac{v_0}{2}=(R+h)^2\frac{\omega}{2},\)
az \(\displaystyle OBC\) idom területe tehát
\(\displaystyle \mathcal{T}=\frac{1}{2}(R+h)^2\omega T.\)
Ezt a területet a geometria alapján is megadhatjuk:
\(\displaystyle \mathcal{T}=\frac{1}{2}R^2\varphi+\frac{2}{3}hR\varphi.\)
Itt magyarázatra szorul a második tag, amely a \(\displaystyle ABC\) idom területe. A valóságban a \(\displaystyle \varphi\) nagyon kicsiny, ezért az \(\displaystyle AC\) körív egy az \(\displaystyle OB\) tengelyre merőleges egyenesnek tekinthető, másrészt a \(\displaystyle BC\) ellipszis ív egy parabola szakasszal közelíthető, amelyről tudjuk, hogy a \(\displaystyle h\) és \(\displaystyle R\varphi\) oldalú téglalap területét 2/3 : 1/3 arányban osztja.
A két kifejezés
\(\displaystyle \frac{1}{2}R^2\varphi+\frac{2}{3}hR\varphi=\frac{1}{2}(R+h)^2\omega T\)
egyenlőségéből \(\displaystyle \tfrac{h}{R}\)-ben vezető rendig
\(\displaystyle \varphi=\frac{(1+\frac{h}{R})^2}{1+\frac{4h}{3R}}\omega T\cong\left(1+\frac{2}{3}\frac{h}{R}\right)\omega T,\)
ahonnan
\(\displaystyle \Delta x=R\varphi-R\omega T=\frac{2}{3}h\omega T.\)
Statistics:
14 students sent a solution. 6 points: Beke Márton Csaba. 5 points: Erdélyi Dominik. 4 points: 2 students. 3 points: 6 students. 2 points: 2 students.
Problems in Physics of KöMaL, March 2025
