Problem P. 5651. (April 2025)

P. 5651. Each side of an insulated equilateral triangle-shaped sheet with uniform surface charge density \(\displaystyle \sigma\) has a length of \(\displaystyle \sqrt{2}a\). What is the value of the electric field strength at the point which is at a distance of \(\displaystyle a\) from each vertex?

(6 pont)

Deadline expired on May 15, 2025.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Jelöljük a kérdéses pontot \(\displaystyle P\)-vel! A töltött háromszög lapnak a \(\displaystyle P\)-n átmenő, a lapra merőleges egyenes egy úgynevezett három fogású szimmetria tengelye, azaz a háromszöget ekörül a tengely körül \(\displaystyle 2\pi/3\)-mal vagy \(\displaystyle 4\pi/3\)-mal elforgatva nem változhat meg a tengelyen mérhető elektromos térerősség. Következésképp annak a tengely irányába kell mutatnia. Tekintsük a háromszög egy kicsiny \(\displaystyle \Delta A\) nagyságú darabját! Ennek a \(\displaystyle \Delta Q=\sigma\Delta A\) töltése a \(\displaystyle P\)-ben olyan \(\displaystyle \Delta E\) térerősséget hoz létre, aminek a lapra merőleges komponense

\(\displaystyle \Delta E_\perp=\Delta E\cos\vartheta=\frac{1}{4\pi\varepsilon_0}\frac{\sigma\Delta A}{r^2}\cos\vartheta.\)

Itt \(\displaystyle r\) a felület darab távolsága \(\displaystyle P\)-től, \(\displaystyle \vartheta\) pedig az adott szakasz irányának a síklap normálisával bezárt szöge, ahogy az ábra mutatja.

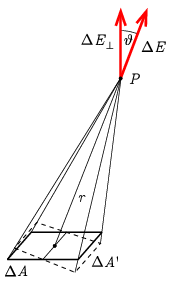
(A \(\displaystyle \Delta E_\parallel=\Delta E\sin\vartheta\) komponensekkel nem kell foglalkoznunk, mert azok eredője az említett szimmetria miatt eltűnik.) Mivel \(\displaystyle \Delta A\cos\vartheta=\Delta A'\) a \(\displaystyle \Delta A\)-nak a \(\displaystyle P\) irányára merőleges vetülete,

\(\displaystyle \frac{\Delta A\cos\vartheta}{r^2}=\Delta\Omega\)

az a térszög, ami alatt a \(\displaystyle \Delta A\) a \(\displaystyle P\)-ből látszik sr-ben (szteradiánban) kifejezve. Így a teljes térerősség

\(\displaystyle E=\frac{\sigma}{4\pi\varepsilon_0}\sum\Delta\Omega=\frac{\sigma}{4\pi\varepsilon_0}\Omega,\)

ahol \(\displaystyle \Omega\) a teljes háromszöghöz tartozó térszög. Könnyen beláthatjuk, hogy a háromszögünk és a \(\displaystyle P\) pont alkotta tetraéder pontosan egy kocka levágott csúcsa, amit a szabályos mellett három egyenlő szárú, derékszögű háromszög alkot. Következésképpen a \(\displaystyle P\)-nél lévő csúcs térszöge a teljes \(\displaystyle 4\pi\) térszög nyolcada, azaz

\(\displaystyle \Omega=\frac{\pi}{2},\)

azaz

\(\displaystyle E=\frac{\sigma}{8\varepsilon_0}.\)

Statistics:

7 students sent a solution.
6 points:	Elekes Panni, Erdélyi Dominik, Kiss 131 Adorján Timon, Papp Emese Petra, Szécsi Bence, Tóthpál-Demeter Márk.
2 points:	1 student.

Problems in Physics of KöMaL, April 2025