 Problem S. 106. (March 2016)
Problem S. 106. (March 2016)
S. 106. We are given a country with \(\displaystyle N\) (\(\displaystyle 1\le N\le 17\)) cities. There are \(\displaystyle M\) cities connected by bidirectional highways. The goal is to organize the maximum number of scientific conferences having different types. A conference of a given type can be organized in more cities, but one city can only host one conference. People in a given city can only visit the conference in their city or in an adjacent city. We would like to organize the maximum number of conference types such that people from any city can visit any conference type. For example, organizing only one type of conference is always possible: each city hosts the same type of conference.
Your program should read the values of \(\displaystyle N\) and \(\displaystyle M\) from the first line of the standard input. The following \(\displaystyle M\) lines describe the highways connecting the cities. The first and only line of the standard output should contain the maximum number of different conference types that can be organized in this country.
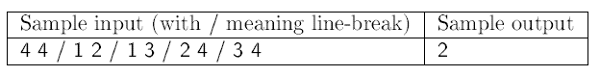
Explanation. Cities 1 and 4 host a conference of type \(\displaystyle A\), while cities 2 and 3 host a conference of type \(\displaystyle B\).
Scoring and bounds. You can get 1 point for a brief and proper documentation clearly describing your solution. Nine further points can be obtained provided that your program solves any valid input within 1 second of running time.
The source code of your program with a short documentation—also describing which developer environment to use for compiling the source—should be submitted in a compressed file s106.zip.
(10 pont)
Deadline expired on April 11, 2016.
Statistics:
6 students sent a solution. 9 points: Gáspár Attila. 5 points: 3 students. 4 points: 1 student. 1 point: 1 student.
Problems in Information Technology of KöMaL, March 2016
