Problem S. 20. (October 2006)

S. 20. Your task is to find a smallest circle that covers n given points in the plane.

Each line of the input text file will contain the X and Y coordinates of a point in the plane, separated by a space. The coordinates are real numbers and may contain decimal points. The input file has no empty lines, the number of lines in the file is equal to the number of points in the plane. The name of the input file is specified in the command line, for example, as

s20.exe data.txt

Your program sends a single line containing the coordinates of the centre of the circle and its radius to the standard output. Data sets having at most 10000 points will be used for testing and evaluating your programs. Speed is also an important factor, an average solution should take no longer than a few minutes.

An example of the data.txt file:

20 10
22.3 8.0
20 2.0

The output in this case is

20.0 6.0 4.0

The source code (s20.pas, s20.cpp, ...) is to be submitted with a short documentation (s20.txt, s20.pdf, ...). (Without any documentation, at most 7 points can be awarded.)

(10 pont)

Deadline expired on November 15, 2006.

Sorry, the solution is available only in Hungarian. Google translation

A megoldás Kezes Balázs érsekújvári diák munkája.

1. Rajzoljunk meg egy kört az összes pont körül. Nyilvánvaló, hogy ezt lehet kisebbíteni.

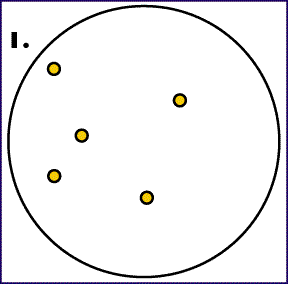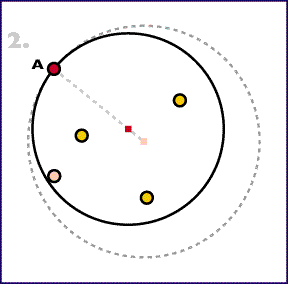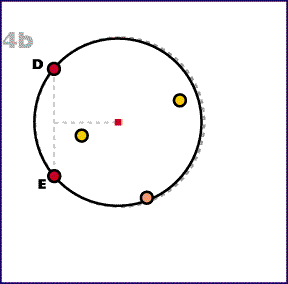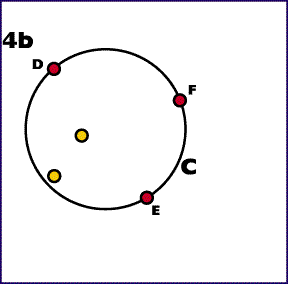
2. Kisebbítsük a kört az olyan A pont megkeresésével, amely a legtávolabb van a középponttól, és rajzoljuk egy új kört ugyanazzal a középponttal és a körvonala haladjon át az A ponton. Ezzel létrehoztunk egy kisebb kört, amelyben szintén benne van az összes pont, de most áthalad az A ponton ahelyett, hogy körülötte lenne.

3. Ha a kör áthalad 2 vagy több ponton, akkor ugorjunk a 4. lépéshez. Ellenkező esetben kisebbítsük a kört a kör közepének az A pont felé valő tolásával, amíg nem érint egy másik B pontot a többi pontból.

4. Ennél a pontnál már van egy körünk, ami kettő vagy több ponton már áthalad. Ha a kör körvonala tartalmaz, egy olyan körív intervallumot, amely nagyobb mint a kör kerületének a fele, és semmilyen pont nem tartózkodik rajta, akkor a kört lehet kisebbíteni. Az ilyen intervallumot pont-mentes intervallumnak fogjuk nevezni. Legyenek a D és E pontok ezen a pont-mentes intervallum végein. Miközben a D és E pontokat a körvonalon tartjuk, kisebbítsük a kör átmérőjét amíg a. az átmérő távolsága nem |DE|, vagy b. a kör körvonala nem érint egy harmadik F pontot.

Az a. esetben végeztünk. A b. esetben meg kell vizsgálnunk, hogy van-e a kerület felénél nagyobb pont-mentes intervallum. Ha nincs, akkor végeztünk. Ellenkező esetben meg a három pontnak egy olyan köríven kell feküdnie, amely rövidebb mint a kerület fele. Meg kell ismételnünk a 4. lépést a két külső ponttal.

Az első három lépés lineárisan függ a pontok mennyisségétől. A 4. lépésben minden új F pont megtalálása is lineárisan függ a pontok mennyisségétől. De az F pont megtalálása nem garantálja az algoritmus végét, és az addig ismétlődik, amíg van pont-mentes intervallum, melynek nagysága nagyobb mint a kerületnek a fele. Legfeljebb (n-2)-ször kell ismételni a 4. lépést, ami O(n²) időbonyolultságot eredményez.

Forrás.

Implementáció

1.-2.: Beolvasáskor csak megnézzük, hogy melyik pont van a legtávolabb az origótól, ez a távolság lesz a kör sugara, az origó pedig a közepe.

3. Most közelítenünk kell a legtávolabbi ponthoz úgy, hogy a kör középpontja az origó és a legtávolabbi ponton áthaladó egyenes maradjon. Definiáljunk egy függvényt (minKör), ami megmondja egy adott egyenesre és két pontra azt a kört, melynek a körvonala áthalad a körön és a középpontja az egyenesen fekszik.

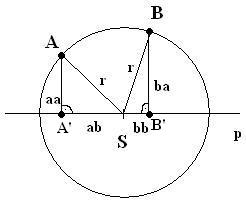
Az a_a és b_a az A és B pontok távolságai a p egyenestől, ezeket ismerjük. A' és B' pontok legyenek az A és B pontok p-re való levetítései. Ezek egymástól való távolságát is ismerjük (legyen ez a d). A kör sugara érdekel minket és az a_b vagy az b_b, hogy meg tudjuk határozni a kör közepét is. Felírhatunk egy háromismeretlenes egyenletrendszert:

a_b+b_b=d

a_a²+a_b²=r²

b_a²+b_b²=r²

Ezt átalakítjuk:

b_b=d-a_b

a_a²+a_b²=b_a²+b_b²

Behelyettesítünk, és azt kapjuk, hogy

Ebből már kitudjuk számolni a kör sugarát, és a középpontot is. A középpontot pedig úgy, hogy normalizáljuk a p egyenes irányvektorát, beszorozzuk az a_b-vel, és az ebből kapott ponthoz hozzáadjuk az A' koordinátáit.

Visszatérve a 3. lépéshez: Annyit kell tennünk, hogy az összes pontra meghívjuk a függvényünket, ahol a másik pont lesz az origótól legtávolabb levő pont, és az egyenes pedig a legtávolabbi ponton és az origón áthaladó egyenes. Az összes sugár közül mi a legnagyobbat fogjunk venni, hisz ez lesz a legkisebb, aminek a közepe az egyenesen van és körbefedi az összes pontot.

4. Az új egyenesünk, amin fogjuk vizsgálni a pontokat, a körvonal két szélső pontján áthaladó egyenesre merőleges lesz, és áthalad a két szélső pont középértékén. Elvileg a legkisebb körnek, amely áthalad ezen két ponton, e két pont távolsága lenne az átmérője, és a kör középpontja a két pont középértéke lenne. Szóval, ha valamelyik pont távolsága ettől a ponttól kisebb, mint az előbb említett kör sugara, akkor felesleges azt megvizsgálni. A maradék pontokra és meghívjuk a minKör függvényünket, ahol az egyenest a bekezdés elején már meghatároztuk, és a másik pont valamelyik szélső pont (mindegy, hogy melyik pont ez, hisz szimmetrikusak az egyenes alapján). Fontos megjegyezni, hogy minden iterációban kisebbítjük a körünket, és ha ezt nem sikerült megtennünk, akkor az azt jelenti, hogy befejeztük.

Itt már megvan a lehető legkiseb kör, ami még mindig behatárolja az összes pontot, és a közepe az adott egyenesen van. Ha ennek az átmérője pontosan a két pont távolsága, akkor végeztünk. Ellenkező esetben lesz egy harmadik pontunk, ami a körvonalon lesz. Meg kell vizsgálnunk, hogy van-e olyan pont-mentes intervallum, amelynek a hossza nagyobb mint kör sugarának a fele. Ezt pedig úgy határozzuk meg, hogy meghatározzuk mind a három pontra, az adott a pont, a kör középpontja és egy köríven felvett tetszőleges pont által bezárt szöget. Ezeket a szögeket sorbarendezzük. Ezután megvizsgáljuk hogy van-e két egymás után következő pont között nagyobb szög mint 180 fok. Ha igen, akkor ez a két pont lesz az új két szélső pont, és ugrunk a ciklus elejére. Ellenkező esetben végeztünk.

5. Kiírjuk az eredményt.

Statistics:

13 students sent a solution.
10 points:	Csernai Kornél, Kezes Balázs, Szebeni Szilveszter.
7 points:	2 students.
4 points:	1 student.
3 points:	4 students.
2 points:	2 students.
1 point:	1 student.

Problems in Information Technology of KöMaL, October 2006