Problem S. 27. (May 2007)
S. 27. Write a program to suggest a next step in a two-player variant of the Minesweeper game in an arbitrary position.
The game is played on a board with N×M squares and having K hidden mines. (Each square contains at most one mine.) At the beginning of the game all squares are covered. Then players alternately uncover a square. If that square contains a mine, the player is awarded one point and can choose another square to uncover. Otherwise we learn the number of adjacent squares (an integer between 0 and 8) containing mines, and it is the other player's turn. The case when there have been no adjacent mines is treated specially: in this case all adjacent squares are automatically uncovered as well, and recursively, every adjacent square with no adjacent mines is also uncovered. Of course, it is the other player's turn in this special case, too.
After the complete board has been uncovered, the player with more points wins.
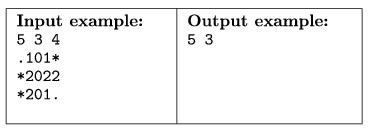
The actual game position should be read from the standard input. The first line of the input contains three integers: the width (N) and height (M) of the board, and the number of hidden mines (K), separated by spaces. Each of the following M lines then contains N characters: the jth character of the (i+1)th line of the input describes the square in the jth column and ith row of the board as follows:
- a dot (.) denotes a covered square
- an asterisk (*) denotes an uncovered square with a mine
- an integer between 0 and 8, if the square has already been uncovered and proved to be clear (the number denotes the number of adjacent mines).
Then your program should suggest a move within 10 seconds and print it to the standard output: two integers X (1
XN) and Y (1YM) separated by a space, representing the column and row indices of the next square to be uncovered.
We will hold a tournament between properly functioning submitted programs. They will play against each other in sets of 10--20 games. The winner of a set is the program winning at least 2/3 of the games. If this ratio is not achieved, the set is a draw. The winner of a set is awarded 3 points, and both players are awarded 1 point if there is a draw. Solutions will be ranked according to these points: the winner program gets 10 points (provided that it is appropriately documented), the second one gets 8 points, the others at most 7 points. If there are only minor differences, there can be more programs on the first and second place.
You may suppose that each input represents a correct game position, further, that N,M100.
The source code of your program (s27.pas, s27.cpp, ...) should be submitted.
(10 pont)
Deadline expired on June 15, 2007.
Sorry, the solution is available only in Hungarian. Google translation
A megoldás menete
A feladat megoldására sok lehetőség kínálkozott, minden esetben a jó megoldás kulcsa az aknák hatékony megtalálása (támadás), illetve ennek eredménytelensége esetén a megfelelő védekezés volt.
Az aknák megtalálására egy kézenfekvő módszer, hogy sorra megvizsgáljuk a számot tartalmazó mezőket, és ha egy ilyen mezőbe írt számérték mínusz a szomszédos aknák száma megegyezik a szomszédos felfedezetlen mezők számával, úgy azok mind aknát rejtenek. Fordítva, ha a számérték a szomszédos aknák számával egyezik meg, úgy minden szomszédos ismeretlen mező aknamentes. Előbbi esetben találtunk egy aknát, utóbbi esetben az újonnan megszerzett információkkal az eljárást újraindíthatjuk.
A módszer előnye, hogy a mezők számával egyenesen arányos időben elvégezhető, ugyanakkor hátránya, hogy nem mindig vezet eredményre.
A hatékonyabb módszerek a problémát olyan lineáris egyenletrendszernek tekintik, ahol a változók (egy ismeretlen mezőn van-e akna), s együtthatóik csak 0/1 értéket vehetnek fel, és minden 'számos' mezőhöz tartozik egy egyenlet, melynek egyik oldalán a szám, másik oldalán 1-együtthatókkal pedig a környező ismeretlen mezők változói szerepelnek. Ezen egyenletrendszer megoldását keressük, illetve, ha az nem egyértelmű, az összes megoldás alapján az egyes mezőkre akna-valószínűségeket határozhatunk meg.
A védekezés akkor kerül előtérbe, amikor nem tudunk biztos aknát mondani, és a valószínűségek is alacsonyak. Célunk, hogy semmiképp se válasszunk nullás mezőt, hiszen ekkor nagy előnyhöz juthat az ellenfél. Itt az alapgondolat, hogy először megpróbálunk egy akna melletti, viszonylag nagy valószínűségű mezőt találni, ha ilyen nincs, akkor szimplán egy akna melletti mezőt, illetve, ha ilyen sincs, akkor véletlenszerűen választhatunk.
A megoldások értékelése
A programok 20x20, 20x100, ill. 100x100 méretű, 10% és 47,5% közti aknasűrűségű mezőkön mérkőztek meg, minden pályán kétszer, egyszer az egyik, egyszer a másik kezdett. Így két program közt összesen 48 különböző pályán 96 mérkőzés zajlott le. Kezes Balázs és Györök Péter jól megoldották a feladatot. Mindkét program - további kiegészítésekkel - az első aknakereső módszerre épült, és tartalmazott védekező logikát is. Györök Péter programja a védekezésben, Kezes Balázs programja pedig a támadásban volt jobb. A ritkás pályákon rendre előbbi, a sűrűbbeken pedig rendre utóbbi győzedelmeskedett, a két nagy pályaméreten a határ olyan éles volt, hogy 30-32.5% sűrűség alatt, illetve felett rendre az egyik, illetve a másik nyert minden fordulót. A végeredmény 53 : 43 (55% : 45%) lett Györök Péter javára, így a feladatkiírás szerint mindkét versenyző munkáját 10 ponttal jutalmaztuk.
Mintamegoldásként letölthető Györök Péter megoldása: s27.zip
Statistics:
2 students sent a solution. 10 points: Györök Péter, Kezes Balázs.
Problems in Information Technology of KöMaL, May 2007