 Problem S. 33. (February 2008)
Problem S. 33. (February 2008)
S. 33. Let us consider the following game. You have to roll a rectangular box of size 2×1×1 along a grid of unit squares, from a given starting square to a final one. Both in its initial and final positions the box stands on the starting/final square on its 1×1 face. At the end of each roll, the box should rest on one of its faces. The rotations are encoded with letters J (=right), B (=left), F (=upper), L (=lower), where ``J'', for example means that the box is rotated by 90o along its right edge if seen from above. The box is allowed to rest only on a selected set of squares.
Write your program to decide whether it is possible to solve the game. If yes, your program should also give the shortest sequence of rotations from the starting to the final position of the box. The shape of the game board is read from a file (its name is given as the first command line argument to your program) and the output is written to another file (with name in the second command line argument).
The first two lines of the input file contain two integers separated by a space: the maximal width S and height M of the board (2 S,M
S,M 100). Each of the following M lines then contains S digits (without spaces): 0, if that square is not part of the game board; 2, if that square is the starting position; 3 for the final position and 1 otherwise.
100). Each of the following M lines then contains S digits (without spaces): 0, if that square is not part of the game board; 2, if that square is the starting position; 3 for the final position and 1 otherwise.
The solution should be encoded as a single line of letters J, B, F or L. If there is no solution, print ``Nem megoldhato''. (In the example, BE means input, while KI means output.)

The source code of your program (s33.pas, s33.cpp, ...) and a short documentation (s33.txt, s33.pdf, ...) should be submitted, containing the main ideas of your solution and the name of the developer environment to run the program.
(10 pont)
Deadline expired on March 17, 2008.
Sorry, the solution is available only in Hungarian. Google translation
A megoldás menete
Először is azt kell meggondolni, hogy miként írjuk le a téglatest pozícióját. Erre egy kézenfekvő megoldás, ha mindig azt nézzük, hogy az adott helyzetben melyik mezőn van a bal felső fele, és erről a mezőről (ha fekszik) merre lóg le. Tehát a téglatestnek van egy koordinátája (azé a mezőé, amin a bal felső fele van), és egy helyzete: áll, jobbra fekszik, lefelé fekszik. Vegyük észre, hogy ha például egy jobbra fekvő téglatestet jobbra gördítünk, x-koordinátája 2-vel növekszik.

Készítsünk egy G gráfot a következő módon: minden mezőhöz vegyünk fel három csúcsot, melyek jelentése: "az adott mezőn álló helyzetben", "az adott mezőn jobbra fekvő helyzetben", "az adott mezőn lefelé fekvő helyzetben". Majd minden csúcsot kössük össze azokkal a csúcsokkal, amelyekbe az adott csúcsban lévő téglatest egyetlen görgetéssel eljuttatható. Tehát pl. a ((x,y), álló helyzet) csúcsot az ((x+1,y), jobbra fekszik), ((x-2,y), jobbra fekszik), ((x,y+1), lefelé fekszik), ((x,y-2), lefelé fekszik) csúcsokkal. Az ábra a középső mezőn lévő álló (felül), jobbra (jobbra), lefelé (alul) helyzethez tartozó csúcsok szomszédait mutatja:
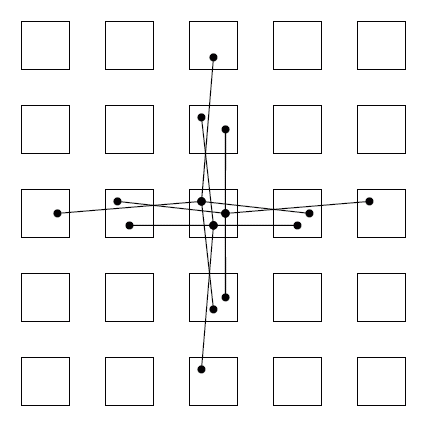
Ha a (kezdőpozíció, álló helyzet)-nek megfelelő csúcsot s-sel, míg a (végpozíció, álló helyzet)-nek megfelelőt t-vel jelöljük, akkor feladatunkat úgy is megfogalmazhatjuk, hogy a G gráfban egy legrövidebb utat keresünk s-ből t-be. Mivel azonban minden élsúly egységnyi, ez nem más, mint egy egyszerű szélességi keresés. Mivel egy konkrét útvonalat is meg kell adnunk, közben tárolnunk kell minden csúcsra azt is, hogy honnan jutottunk oda.
A szélességi bejárás műveletigénye , ahol p a gráf csúcsainak, e pedig éleinek száma. Esetünkben p=3.S.M, ugyanakkor tudjuk, hogy 1 csúcsnak legfeljebb 4 szomszédja van, hiszen legfeljebb 4 irányba léphetünk. Ezért e<=2p. Így az algoritmus műveletigénye
, a mezők számában lineáris (tárigénye úgyszintén).
Mintamegoldás
A C++ nyelven készült mintamegoldás letölthető az alábbi linkre kattintva:
Engedy Balázs
Statistics:
2 students sent a solution. 6 points: 1 student. 5 points: 1 student.
Problems in Information Technology of KöMaL, February 2008
