Problem S. 49. (December 2009)

S. 49. People in a remote country care for the environment and are planning to use vehicles powered by hydrogen. Liquid hydrogen is stored in safety tanks, unfortunately however, there are still only few hydrogen stations. Hydrogen cars can operate in regions where hydrogen stations are at most K km apart from each other. Note however that they use the following metric in the coordinate plane: the distance of two points is the sum of absolute value of differences of the corresponding coordinates, |x₁-x₂|+|y₁-y₂|.

Your task is to group hydrogen stations: two stations will be in one group if one can travel between the two stations by touching stations in the group being at most K km apart. Your program should compute the number of these groups, further, give which stations are part of one group.

The first command line argument to your program is the name of the input file. The first line of this file gives the number of hydrogen stations N (3N200), further the value of K (100K500). The following N lines then contain the x, y (0x,y1000) coordinates of the stations.

The second command line argument to your program is the name of the output file. The first line of the output file should contain the number of groups, G, and the next G lines should list the codes of hydrogen stations in one group, separated by a space.

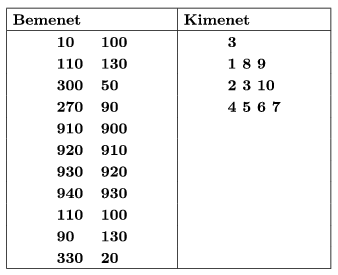
In the example, ``Bemenet'' is input, while ``Kimenet'' is output.

The source code and project files of your solution -- without the .exe or any other auxiliary files generated by the compiler -- should be submitted together with a short documentation in a compressed folder s49.zip.

(10 pont)

Deadline expired on January 11, 2010.

Sorry, the solution is available only in Hungarian. Google translation

Megoldásokról

Sok tökéletes megoldás érkezett a feladatra. A gráfok bejárását ismerőknek nem jelentett problémát a megoldás.

Mintamegoldás

Borsos Zalán (Marosvásárhely, Bolyai Farkas Elméleti Líceum, 11. osztály) megoldása alapján

A program kiszámítja minden kút pár közti távolságot (O(n² ) ), majd a következő gondolatmenetet követi: legyen egy gráf, amelynek csúcspontjai az N darab töltőállomás. Él van az i és j töltőállomás között, ha köztük a távolság kisebb vagy egyenlő, mint k. A feladatunk így a gráf összefüggő komponenseinek a meghatározása, amelyet egy mélységi bejárással oldunk meg csúcs-szomszédsági mátrixból.

s49.cpp

Statistics:

19 students sent a solution.
10 points:	Adrián Patrik, Borsos 607 Zalán, Éles András, Élő Dániel, Énekes Péter, Hunyady Márton, Iglói Gábor, Mokcsay 026 Ádám, Nagy 111 Miklós, Németh Bence, Ofella Norbert, Szabó 928 Attila, Weisz Ágoston, Weisz Gellért.
8 points:	2 students.
5 points:	1 student.
0 point:	2 students.

Problems in Information Technology of KöMaL, December 2009