 Problem S. 52. (March 2010)
Problem S. 52. (March 2010)
S. 52. In the figure you see a lake in which a snake is hiding. The snake winds only horizontally and vertically. (There are no parts of the snake for which the corresponding squares have a common vertex only.) Black squares are rocks and the snake can not pass them. Numbers below the figure denote how many squares in the actual column contain squares that are part of the snake. The head and the tip of the tail of the snake are above the water level, so we can spot those.
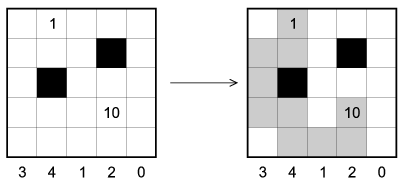
Your program should give the complete position of the snake in the lake. The first command line argument to your program is the name of the file containing known data for the lake and the snake. The first line of this file describes the side length N (3 N
N 20) of the square-shaped lake and the length of the snake M (3
20) of the square-shaped lake and the length of the snake M (3 M), while the four numbers E1, E2, V1 and V2 (1
M), while the four numbers E1, E2, V1 and V2 (1 E1,E2,V1,V2
E1,E2,V1,V2 N) in the second line give the coordinates of the head and the tail of the snake.
N) in the second line give the coordinates of the head and the tail of the snake.
The number of rocks in the lake K (0 K
K N) is given in the third line. The following K lines then contain two integers: coordinates of each rock. The last line contains N numbers: the number of snake-parts in each column.
N) is given in the third line. The following K lines then contain two integers: coordinates of each rock. The last line contains N numbers: the number of snake-parts in each column.
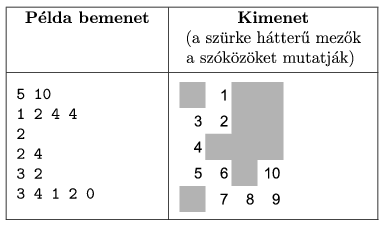
The second command line argument to your program is the name of the output file. It should contain N lines depicting the lake and the position of the snake. Each square of the lake should occupy 3 characters. Water in the lake is denoted by spaces (this is seen as grey squares in the example). Body of the snake is denoted by integers: corresponding distances from its head. If this puzzle has no solution, then the content of the output file should be ``No solution''.
In the example, ``Példa bemenet'' is the sample input, while ``Kimenet'' is the output.
The source code (s52.pas, s52.cpp, ...) together with a documentation (s52.txt, s52.pdf, ...) -- also describing which developer environment to use for compiling, further a brief description of your solution -- should be submitted in a compressed file (s52.zip).
The idea of this exercise is taken from the web page of Hungarian logic puzzles.
(10 pont)
Deadline expired on April 12, 2010.
Sorry, the solution is available only in Hungarian. Google translation
Megoldásokról
Nagy Miklós (Győr, Révai Miklós Gimnázium) 11. osztályos tanuló megoldása alapján
A program a kígyó helyzetének megkereséséhez a visszalépéses keresés módszerét alkalmazza. A kígyó farkától visszafele haladva keresi meg a kígyó testének lehetséges helyzeteit.
A tó adatai a viz mátrixban vannak tárolva, melyben a számok jelentése a következő: 0- víz és 1- kő. A nagyobb számok a kígyó testét jelölik, méghozzá a kígyó fejétől mért távolság plusz 3-at. A plusz 3 a víztől és a kőtől való megkülönböztethetőséget szolgálja.
A keresés folyamán a kígyó farkától indulunk visszafele a fejéhez. A faroktól való indulás teszi lehetővé, hogy a kígyót a kövektől egyszerűbben tudjuk megkülönböztetni. A soron következő pont megkeresését a tekereg eljárás végzi. Ez addig keresi a lehetséges elhelyezéseket, amíg az 1-es sorszámú testdarab a fej pozíciójába kerül vagy amíg az összes lehetséges esetet végignézi (ha nincs megoldás). A következő testrész megkeresésénél 4 lehetséges eset van, ezek közül mindig a sorszám szerint első lehetséges lépést hajtja végre. A következő lépés feltételei: A kijelölt mező a tóban legyen és ne legyen kő. A kijelölt mező 8 szomszédja közül max 2 kígyórész lehet, és ez a két rész a fejtől mért távolságban is a két legközelebbi lehet, ellenkező esetben a kígyó érintené önmagát, ami a feladat szerint nem lehetséges. A lépendő oszlopba van-e még hely még egy résznek, az elején megadott testrészszámok szerint alapján?
Ha a lépés lehetséges, akkor végrehajtja, ha pedig egyik irányba sem tud tovább haladni, akkor visszalép az előző pozícióra és visszaállítja a pálya megfelelő értékeit.
Ha megvan a kígyó pozíciója, akkor kiírja azt a megadott célfájlba. s52.pas
Tesztállományok: k1.be k2.be k3.be
Statistics:
13 students sent a solution. 10 points: Adrián Patrik, Borsos 607 Zalán, Fekete 976 János, Mokcsay 026 Ádám, Nagy 111 Miklós, Weisz Ágoston, Weisz Gellért. 9 points: Éles András. 8 points: 2 students. 5 points: 2 students. Unfair, not evaluated: 1 solutions.
Problems in Information Technology of KöMaL, March 2010
