 Problem S. 80. (April 2013)
Problem S. 80. (April 2013)
S. 80. Big Bird often visits his friends in a city of N inhabitants. In this city, all streets are one-way. Big Bird does not like walking too much, so, as a first question, he wondered how many and which streets he can use to walk to one of his friends (Big Bird has N-1 friends, since everybody is his friend) such that the distance covered is as small as possible. He then raised a second, harder question: ``what is the number of shortest possible ways from my house to one of my friends' house?''
Your program should read the values of N and M from the first line of the standard input (), denoting the number of houses and streets. Then, from the next M lines it should read the integers ki, vi, si (separated by a space) describing the streets: the first house in the ith street is ki, the last house is vi, and the street length is si. Big Bird lives in house #1. The first line of the standard output should contain the integer a, being the number of streets answering his first question. The next line should contain these a streets in increasing order, separated by a space (their number is specified by their position in the input file). The last line of the output should contain the answer to the second question, that is, the number of ways to each of his friends' house via a shortest route (more precisely, the remainder of this integer upon division by 1000007).
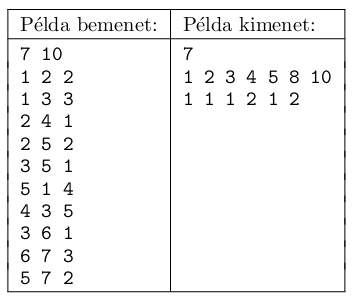
``Példa bemenet'' contains a sample input, while ``Példa kimenet'' is the corresponding output.
Scoring and bounds. You can obtain 1 point for a brief and proper documentation clearly describing your solution. The remaining maximal 9 points for your program can only be obtained if it can solve an arbitrary valid input within 1 second of running time. Partial points of the above 9 points can be obtained if your program can solve only smaller test cases within the allotted time. Your program will only score points if it produces correct outputs in at least 20% of the inputs corresponding to the first task.
The source code (s80.pas, s80.cpp, ...) without the .exe or any other auxiliary files generated by the compiler but with a short documentation (s80.txt, s80.pdf, ...) - also describing which developer environment to use for compiling - should be submitted in a compressed file s80.zip.
(10 pont)
Deadline expired on May 10, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás
A Dijkstra algoritmussal megkeressük a kezdőpontból az összes minimális távolságot: d(v). Ezután definiáljuk pontos éleknek azokat az uv éleket, melyekre d(v)-d(u)=s(uv), ahol s(uv) az uv él hossza. Miért is jó ez, illetve mit is jelent ez? Azt jelenti, hogy ha ezen az élen végigmegyünk, akkor ha az u pontig egy minimális úton mentünk, akkor hozzátéve ezt az élet szintén minimális utat kapunk, mert a Dijkstra a minimális távolságokat adta meg, és az egyenlőség miatt pont ezt kapjuk az utunk hosszának. Tehát a pontos élek lesznek a megoldás az első kérdésre. Már csak a második kérdésre kell válaszolni. Vegyük a pontos élek részgráfját. Ugye ha nem pontos élen megyünk, akkor az egyenlőség nem teljesül, emiatt nem kaphatunk minimális utat. Így már csak azt kell eldönteni, hogy ebben a részgráfban a kezdőponttól az egyes pontokig hányféleképpen juthatunk el. Ezt többféleképp is megoldhatjuk: topologikusan rendezzük a csúcsokat (a gráf körmentes, mert ha lenne benne kör pontos élekből, akkor minden él súlya 0 kellene, hogy legyen), majd sorrendben végigmegyünk rajtuk. Ekkor könnyen frissíthetjük, hogy az aktuális csúcsba hányféleképp juthatunk el, hiszen csakis az őt megelőzőekből juthatunk el oda (topologikus rendezés miatt), azt meg már kiszámoltuk. Pontosabban az összes bele mutató él kezdőpontján kell összeadnunk a számokat.
Mi is az a topologikus rendezés? Van egy körmentes irányított gráfunk. Szeretnénk úgy sorba rendezni a csúcsokat, hogy csak jobbra mutassanak az élek. Erre a következő az algoritmus: mélységi bejárással elhagyási idő szerint (amikor már az összes leszármazottját bejártuk) rendezzük a csúcsokat. Ez pont jó lesz.
Mintamegoldás: main.cpp
Statistics:
6 students sent a solution. 10 points: Szabó 928 Attila. 8 points: 1 student. 4 points: 1 student. 2 points: 2 students. 1 point: 1 student.
Problems in Information Technology of KöMaL, April 2013
