 Problem S. 87. (February 2014)
Problem S. 87. (February 2014)
S. 87. A group called Reformers of Mathematics made a huge discovery and created a new definition. The New Greatest Common Divisor, henceforth abbreviated as ngcd, of a finite sequence of natural numbers is defined as the number of elements of the sequence multiplied by the old-fashioned gcd of the sequence. The Reformers of Mathematics immediately give you the following task.
You are given a sequence of positive integers (a1,...,aN) with . Determine the maximal possible ngcd over all subsequences formed by any consecutive elements of the original sequence.
Your program should read the value of N from the first line of the standard input, then the numbers ai (1 ai
ai 1011) from the next line. The first and only line of the standard output should contain the maximal positive integer that represents the ngcd of a connected subsequence of the given sequence.
1011) from the next line. The first and only line of the standard output should contain the maximal positive integer that represents the ngcd of a connected subsequence of the given sequence.
In the example, ``Példa bemenet'' and ``Példa kimenet'' denote a sample input and output, respectively.
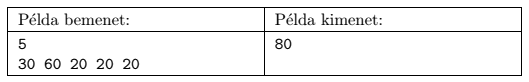
Scoring and bounds. You can obtain 1 point for a brief and proper documentation clearly describing your solution. Nine further points can be obtained provided that your program solves any arbitrary valid input within 1 second of running time. Partial points can be obtained if your program yields a solution for N 200, or for N
200, or for N 5000.
5000.
The source code (s87.pas, s87.cpp, ...) without the .exe or any other auxiliary files generated by the compiler but with a short documentation (s87.txt, s87.pdf, ...), also describing which developer environment to use for compiling the source, should be submitted in a compressed file s87.zip.
(10 pont)
Deadline expired on March 10, 2014.
Sorry, the solution is available only in Hungarian. Google translation
Mintamegoldásnak Somogyvári Kristóf megoldását tesszük közzé. A feladatnak ez az ismert leggyorsabb megoldása, intervallumfával - okosan lehet kicsit lassabbat, illetve nem olyan nagyon okosan kb 10-ed ilyen lassút. S87.zip
Statistics:
15 students sent a solution. 9 points: Weisz Ambrus. 7 points: 1 student. 5 points: 4 students. 4 points: 3 students. 3 points: 2 students. 2 points: 1 student. 0 point: 1 student. Unfair, not evaluated: 2 solutionss.
Problems in Information Technology of KöMaL, February 2014
