 Problem S. 88. (March 2014)
Problem S. 88. (March 2014)
S. 88. We are given an undirected graph with N vertices (1 N
N 100000) and M (1
100000) and M (1 M<N) edges. You should determine the number of ways the edges can be directed so that every vertex has at most one outward edge. You should then give the remainder on division of this number by 1000000007.
M<N) edges. You should determine the number of ways the edges can be directed so that every vertex has at most one outward edge. You should then give the remainder on division of this number by 1000000007.
The values of N and M should be read from the first line of the standard input. Then the integers ai and bi (1 ai,bi
ai,bi N) separated by a space should be read from the following M lines. Each (ai,bi) pair represents an undirected edge in the graph between vertices ai and bi.
N) separated by a space should be read from the following M lines. Each (ai,bi) pair represents an undirected edge in the graph between vertices ai and bi.
Since the graph is not necessarily simple, certain (ai,bi) pairs can appear more than once in the input. The first and only line of the standard output should contain the number of possibilities modulo 1000000007.
In the example, ``Példa bemenet'' is a possible input and ``Példa kimenet'' is the corresponding output.
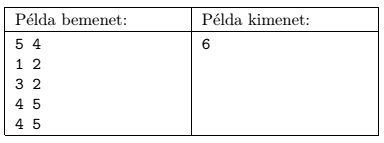
Scoring and bounds. You can obtain 1 point for a brief and proper documentation clearly describing your solution. Nine further points can be obtained provided that your program solves any arbitrary valid input within 1 second of running time. Partial points can be obtained if your program yields a solution
for N
 200, or
200, or
for N
 5000.
5000.
The source code (s88.pas, s88.cpp, ...) without the .exe or any other auxiliary files generated by the compiler but with a short documentation (s88.txt, s88.pdf, ...), also describing which developer environment to use for compiling the source, should be submitted in a compressed file s88.zip.
(10 pont)
Deadline expired on April 10, 2014.
Sorry, the solution is available only in Hungarian. Google translation
Mintamegoldásnak Makk László megoldását tesszük közzé. Oda kellett figyelni arra, hogy a gráfban lehetnek hurokélek is! s88.zip
Statistics:
12 students sent a solution. 10 points: Makk László, Somogyvári Kristóf, Weisz Ambrus, Zalavári Márton. 9 points: Alexy Marcell. 8 points: 1 student. 6 points: 1 student. 4 points: 1 student. 3 points: 2 students. 2 points: 1 student. 0 point: 1 student.
Problems in Information Technology of KöMaL, March 2014
