Problem S. 95. (January 2015)

S. 95. George has five identical decks of playing cards. Each card contains an integer, and no integer is found on two different cards in a deck. So if a particular number turns up in a deck, then that number can also be found in each of the other decks exactly once. George likes to keep his cards in a particular order: he ordered all five decks in the same way.

During the night, however, a wicked kobold visited George's house. The kobold chose a deck and drew some cards out of it, then put those cards back into the deck in some way (not necessarily to their original place, but into the same deck). The kobold then performed this operation on each of the remaining four decks. But if a particular integer was relocated in a deck, the corresponding card with that integer was not touched again in the other decks. After waking up in the morning, George was perplexed. Fortunately, you can help him restore the original card order in all decks.

Your program should read the value of \(\displaystyle N\) (\(\displaystyle 1\le N\le 50\;000\)) from the first line of the standard input, then the (space-separated) \(\displaystyle a_i\) integers from the following \(\displaystyle 5\cdot N\) lines. The first \(\displaystyle N\) numbers describe the card order in the first deck after the kobold's operation, the second \(\displaystyle N\) numbers describe the new card order in the second deck, and so on. The first \(\displaystyle N\) lines of the standard output should contain the original, common deck order.

In the example, ``Példa bemenet'' is a sample input, and ``Példa kimenet'' is the corresponding output. To save some space in the example, the \(\displaystyle 5\cdot N\) input lines and the \(\displaystyle N\) output lines are now printed in one line, with the / symbol denoting end-of-line characters.

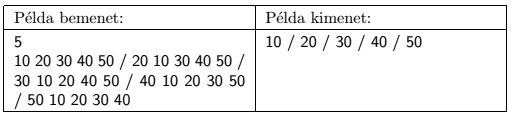
Scoring and bounds. You can obtain 1 point for a brief and proper documentation clearly describing your solution. Nine further points can be obtained provided that your program solves any arbitrary valid input within 1 second of running time.

The source code (s95.pas, s95.cpp, ...) without the .exe or any other auxiliary files generated by the compiler but with a short documentation (s95.txt, s95.pdf, ...), also describing which developer environment to use for compiling the source, should be submitted in a compressed file s95.zip.

(10 pont)

Deadline expired on February 10, 2015.

Statistics:

14 students sent a solution.
10 points:	Csenger Géza, Fuisz Gábor, Gáspár Attila, Juhász 326 Dániel, Kiss Gergely, Németh 123 Balázs, Zalavári Márton, Zarándy Álmos.
9 points:	Weisz Ambrus.
7 points:	1 student.
5 points:	1 student.
3 points:	1 student.
2 points:	1 student.
1 point:	1 student.

Problems in Information Technology of KöMaL, January 2015