A KöMaL 2011. januári matematika feladatai

Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.

Feladat típusok elrejtése/megmutatása:

K-jelű feladatok

A beküldési határidő 2011. február 10-én LEJÁRT.

K. 277. Pisti gondolt egy pozitív egész számra, és a következő igaz állításokat mondta róla:

Ha a gondolt szám osztható 3-mal, akkor 50 és 59 között van.

Ha a gondolt szám nem osztható 4-gyel, akkor 60 és 69 között van.

Ha a gondolt szám nem osztható 6-tal, akkor 70 és 79 között van.

Melyik számra gondolt Pisti?

(6 pont)

megoldás, statisztika

K. 278. Az alábbi két ábrán szabályos sokszögek (most megengedjük a csillagsokszögeket is) vannak összeillesztve egy-egy csúcsuknál. Tényleg mindkét esetben illeszkednek a sokszögoldalak egymásra, vagy valamelyik ábra ,,csal''?

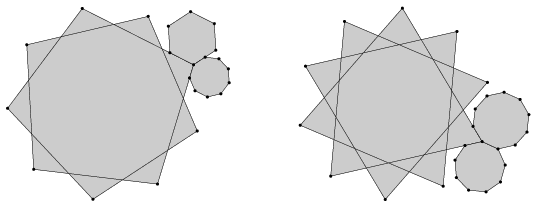
(6 pont)

megoldás, statisztika

K. 279. Anna, Bea, Csilla és Dóri 52 lapos kártyacsomaggal kártyázott. Az egyik körben Dóri osztott. Egyesével adta a lapokat a résztvevőknek Anna, Bea, Csilla és Dóri sorrendben, amikor hirtelen kiesett néhány kártya a kezében levő, még kiosztatlan lapok közül a padlóra. Észrevették, hogy a padlón levő lapok darabszáma éppen az Annának már kiosztott lapok darabszámának 2/3 része, a Csillának már kiosztott lapok darabszáma pedig a Dóri kezében maradt, még ki nem osztott lapok darabszámának 2/3 része. Hány lapot osztott már ki Dóri összesen?

(6 pont)

megoldás, statisztika

K. 280. Keressük meg azt a legkisebb (2^a3^b7^c alakú) pozitív természetes számot, amelynek a fele egy egész szám köbe, a harmada egy egész szám hetedik hatványa, a hetede pedig egy egész szám négyzete.

(6 pont)

megoldás, statisztika

K. 281. Dominikának olyan dominókészlete van, amiben a legkisebb dominó a dupla 1-es, a legnagyobb a dupla 6-os, és közte minden párosításból 1 db van. Dominika rájött, hogy a dominókkal bizonyos törtszámokat is szemléltethet, ha a felső félen lévő szám a számláló, az alsó félen lévő a nevező. Dominika leült húgával, Noémival szemben, és az itt látható osztást rakta ki dominókból.

(6 pont)

megoldás, statisztika

K. 282. Gyufaszálakból raktunk ki egy háromszöget. A háromszög oldalainak hossza 13, 20, illetve 21 gyufaszál. Adjuk meg (ha van) a háromszög azon magasságainak hosszát, amelyek kirakhatók egész gyufaszálakból.

(6 pont)

megoldás, statisztika

C-jelű feladatok

A beküldési határidő 2011. február 10-én LEJÁRT.

C. 1060. Legyen n egy 3-mal osztható szám. Az n-1, n-2, ..., 2, 1 sorozat minden harmadik tagját hagyjuk el. A megmaradó sorozatban két tagonként haladva adjunk a tagpároknak felváltva pozitív, majd negatív előjelet: +(n-1), +(n-2), -(n-4), -(n-5), ... . Bizonyítsuk be, hogy az így kapott számok összege n.

(5 pont)

megoldás, statisztika

C. 1061. Szerkesszük meg az ABC háromszöget, ha adott az AB oldalának felezőpontja, az AC oldalhoz tartozó magasság talppontja és az A csúcsnál levő $\alpha$ szöge.

(5 pont)

megoldás, statisztika

C. 1062. Egy dobókockával n-szer dobunk. Mekkora annak a valószínűsége, hogy a dobott számok között van két egyenlő?

(5 pont)

megoldás, statisztika

C. 1063. Egy épület egyik oldala 20 méter oldalhosszúságú négyzet. A vízszintes talaj két pontjából megmértük a függőleges élek látószögeit. Ezek az egyik pontból 40^o és 38^o, a másik pontból 32^o és 40^o. Milyen távolságra van egymástól a két észlelési hely?

(5 pont)

megoldás, statisztika

C. 1064. Az x, y, z valós számok egy nem konstans számtani sorozat egymást követő tagjai, melyekre teljesül, hogy

$\cos x + \cos y + \cos z & = 1,$

$\sin x + \sin y + \sin z & = \frac{1}{\sqrt 2}.$

Mennyi a sorozat 12. tagjának tangense, ha az első tag x volt?

(5 pont)

megoldás, statisztika

B-jelű feladatok

A beküldési határidő 2011. február 10-én LEJÁRT.

B. 4322. Egy állásinterjúra öt embert hívnak be, öt előre adott lehetséges időpontra. Minden jelentkező egy adatlapon megjelöl az öt időpontból kettőt. Mi a valószínűsége, hogy mindenkit meg tudnak hallgatni az egyik általa megjelölt időpontban?

Javasolta: Holló Gábor (Budapest)

(4 pont)

megoldás, statisztika

B. 4323. Oldjuk meg a következő egyenletet:

$\frac{1+x^4}{{(1+x)}^4} = \frac{3}{4}.$

(3 pont)

megoldás, statisztika

B. 4324. Az ABC háromszögben az A-ból induló magasságvonal talppontja D, a B-ből induló magasságvonal felezőpontja E, továbbá a C-ből induló magasságvonal felezőpontja F. Mutassuk meg, hogy $EDF\sphericalangle =CAB\sphericalangle$ .

Javasolta: Miklós Szilárd (Herceghalom)

(4 pont)

megoldás, statisztika

B. 4325. a) Igaz-e, hogy bármely ABC háromszög tetszőleges P belső pontjára fennáll a PA+PB<CA+CB egyenlőtlenség?

b) Igaz-e, hogy bármely ABCD tetraéder tetszőleges P belső pontjára fennáll a PA+PB+PC<DA+DB+DC egyenlőtlenség?

(5 pont)

megoldás, statisztika

B. 4326. Legyenek a és b egész számok. Adjunk meg olyan c és d egészeket, amelyekre tetszőleges n egész szám esetén az an+c relatív prím bn+d-hez.

(5 pont)

megoldás, statisztika

B. 4327. Szerkesszünk egyenlő szárú háromszöget, ha adott az egyik szárhoz tartozó súlyvonala és e súlyvonalnak a másik szárral bezárt szöge.

(4 pont)

megoldás, statisztika

B. 4328. Adottak az a és b oldalú szabályos ötszögek. Ha az a oldalú ötszöget megforgatjuk az egyik oldala körül, akkor a keletkezett test térfogata egyenlő annak a testnek a térfogatával, melyet a b oldalú ötszög egyik átlója körüli forgatásával kapunk. Határozzuk meg az a:b arányt.

(3 pont)

megoldás, statisztika

B. 4329. Írjuk fel sin ( $\pi$ /2²⁰¹¹) pontos értékét az 1 és 2 számjegyek, valamint az alapműveletek és négyzetgyökjelek segítségével.

(4 pont)

megoldás, statisztika

B. 4330. Melyik az a kétváltozós p polinom, amelyre

$p(x+y,xy) =\sum_{k=0}^{20}x^{20-k}y^{k}?$

Javasolta: Hraskó András (Budapest)

(4 pont)

megoldás, statisztika

B. 4331. Mutassuk meg, hogy ha a $\mathcal{K}$ konvex sokszögnek P belső pontja, akkor megadható a síkon négy egyenes úgy, hogy $\mathcal{K}$ bármely oldalszakaszához van az adott egyenesek közt olyan, amely által meghatározott két nyílt félsík egyike P-t, másika pedig az oldalszakaszt tartalmazza. Igaz-e az állítás, ha csak három egyenest adhatunk meg?

Javasolta: Vígh Viktor (Calgary)

(5 pont)

megoldás, statisztika

A-jelű feladatok

A beküldési határidő 2011. február 10-én LEJÁRT.

A. 524. Felbontható-e az {1,2,...,2010} halmaz páronként diszjunkt, ötelemű halmazokra úgy, hogy az elemek összege mindegyik ötelemű halmazban osztható legyen 2011-gyel?

(5 pont)

megoldás, statisztika

A. 525. Legyen $f(x)=x^n+a_{n-1}x^{n-1}+\ldots+a_1x+a_0$ egész együtthatós polinom, $d_1,\ldots,d_n$ pedig páronként különböző egész számok. Tegyük fel, hogy végtelen sok p prímhez létezik olyan k_p egész szám, amelyre

$f(k_p+d_1)\equiv f(k_p+d_2)\equiv \dots\equiv f(k_p+d_n)\equiv 0 \pmod{p}.$

Igazoljuk, hogy ekkor van olyan k₀ egész szám, amire

$f(k_0+d_1)=f(k_0+d_2) =\ldots=f(k_0+d_n)=0.$

(5 pont)

megoldás, statisztika

A. 526. A síkbeli koordináta-rendszerben nevezzük sávnak az olyan tartományokat, amelyeket két párhuzamos egyenes határol. Egy sáv szélessége legyen a beleírható, a tengelyekkel párhuzamos oldalú négyzetek oldalhossza. Igazoljuk, hogy ha a 0 $\le$ x,y $\le$ 1 egységnégyzetet lefedjük véges sok sávval, akkor ezek szélességének összege legalább 1.

(5 pont)

statisztika

A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:

megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.

(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

Már regisztráltál?
Új vendég vagy?