A KöMaL 2018. szeptemberi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2018. október 10-én LEJÁRT. |
M. 379. Mérjük meg, milyen magasságból kell függőlegesen leejteni egy rugós golyóstollat, hogy az íróhegye ennek következtében kipattanjon! Ha már kipattant, milyen magasságból kell függőlegesen leejteni, hogy a hegye visszapattanjon?
Varga István (1952-2007) feladata
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2018. október 10-én LEJÁRT. |
G. 641. Az ábrán látható csigasorban a csigák tömege 1 kg. Mekkora \(\displaystyle F\) erő szükséges ahhoz, hogy a ketreccel együtt 9 kg tömegű majmot egyensúlyban tartsuk?
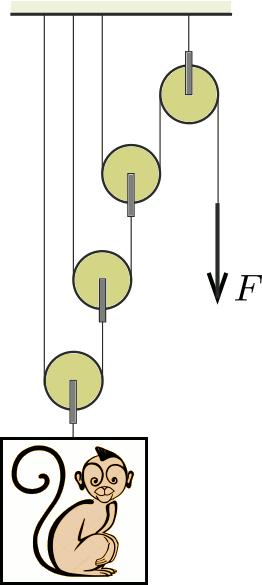
(3 pont)
G. 642. Egy \(\displaystyle 2R\) sugarú kör kerületének belső oldalán csúszásmentesen gördül körbe egy \(\displaystyle R\) sugarú kerék. Milyen pályán mozog a kis kerék egy kerületi pontja?
(3 pont)
G. 643. Egy karos mérlegen egy vizet tartalmazó edény van kiegyensúlyozva. Megbomlik-e a mérleg egyensúlya, ha egyik ujjunkat bemerítjük a vízbe úgy, hogy az edényhez nem érünk hozzá? Milyen választ adhatunk a kérdésre, ha
a) egy csepp víz sem folyik ki az edényből;
b) a színültig töltött edényből kifolyó víz lecsurog a mérleg tányérja mellett?
(3 pont)
G. 644. Az ábrán látható kapcsolásban négy egyforma villanykörtét kötöttünk a telepre. Melyik világít legerősebben? Rakjuk sorba az izzókat fényerejük szerint!
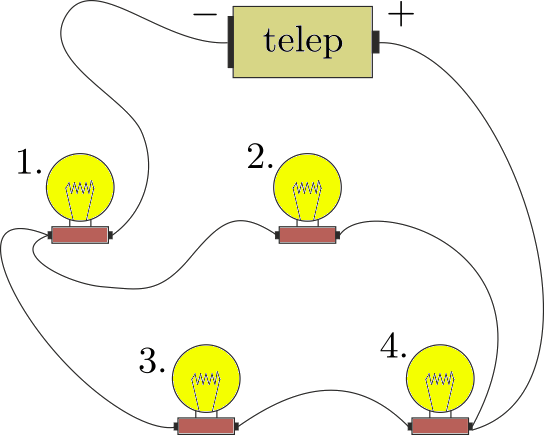
(3 pont)
 |
P-jelű feladatokA beküldési határidő 2018. október 10-én LEJÁRT. |
P. 5045. A Holdon egy szabadon eső test teljes esési magassága \(\displaystyle n\)-szer nagyobb, mint az utolsó másodpercben megtett útja. Határozzuk meg az esés magasságát és az esés idejét!
Faragó Andor (1877-1944) feladata nyomán
(4 pont)
P. 5046. Egy \(\displaystyle M\) tömegű deszkát az ábrán látható módon, szimmetrikus elrendezésben rögzítünk. Az állócsigák és a kötelek tömege, valamint a tengelysúrlódás elhanyagolható. (A \(\displaystyle m\) tömegű testek nincsenek a \(\displaystyle M\) tömegű deszkához ragasztva.)
Milyen \(\displaystyle m/M\) arány esetén lehet egyensúlyban a rendszer?
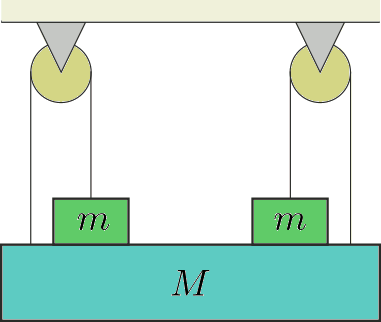
Közli: Nagy Piroska Mária, Dunakeszi
(3 pont)
P. 5047. Az ábrán látható \(\displaystyle M\) tömegű kiskocsi és a rajta levő lapos, \(\displaystyle m\) tömegű hasáb \(\displaystyle v\) sebességgel halad a falhoz rögzített, \(\displaystyle D\) rugóállandójú nyomórugó felé. A hasáb és a kiskocsi felülete közötti súrlódási együttható \(\displaystyle \mu\).
a) Ütközéskor megcsúszik-e a hasáb?
b) Mennyi ideig tart az ütközés?
Adatok: \(\displaystyle M=0{,}2~\rm kg\), \(\displaystyle m=0{,}1~\rm kg\), \(\displaystyle v=1\) m/s, \(\displaystyle D=4{,}4~\)N/m, \(\displaystyle \mu=0{,}4\).
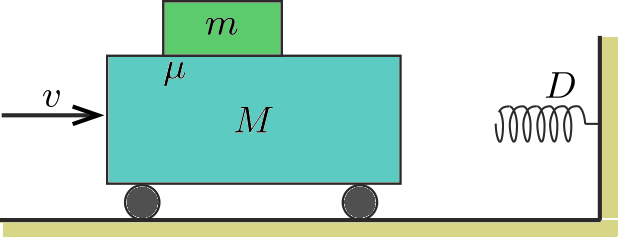
Közli: Németh László, Fonyód
(4 pont)
P. 5048. Becsüljük meg, mekkora nyomáskülönbség alakul ki egy (álló helyzetben mondjuk 2 bar túlnyomású) autóguminak az abroncsnál lévő ,,belső'' és a futófelületénél lévő ,,külső'' része között! Az autópályán a megengedett maximális sebesség 130 km/h.
Közli: Tichy Géza, Budapest
(4 pont)
P. 5049. Legalább mekkora sebességgel kell elindítani egy rakétát a Földről, hogy eljusson a Holdra? Hasonlítsuk össze ezt a sebességet a második kozmikus sebességgel! (Az egyszerűség kedvéért a Föld és a Hold mozgását ne vegyük figyelembe!)
Közli: Cserti József, Budapest
(5 pont)
P. 5050. Egy zárt edényben víz, a víz felett vízgőz van. Mi történik a vízzel, ha a vízgőzt szivattyúzni kezdjük, miközben a víz hőmérsékletét állandónak tartjuk, ha ez a hőmérséklet
a) \(\displaystyle 100{,}00\,^\circ\)C;
b) \(\displaystyle 20{,}00\,^\circ\)C?
Közli: Radnai Gyula, Budapest
(3 pont)
P. 5051. Héliumgáz állapota az ábrán látható módon változik. Mekkora a folyamat során felvett hő?
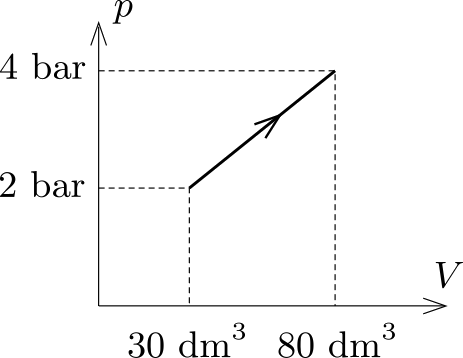
Példatári feladat
(4 pont)
P. 5052. 1,5 cm vastag üveglemez alatt kicsiny szemcse fekszik. Hol keletkezik a szemcse látható képe, ha a látósugár merőleges a lemez felületére, és az üveg törésmutatója \(\displaystyle n=1{,}5\)?
Példatári feladat
(3 pont)
P. 5053. Határozzuk meg egy olyan csillag teljes fényteljesítményét, amelynek felszíni hőmérséklete 7500 K, átmérője pedig a Nap átmérőjének 2,5-szerese. A Nap felszíni hőmérsékletét vegyük 5800 K-nek, fényteljesítményét tekintsük egységnyinek.
Csillagászati versenyfeladat nyomán
(4 pont)
P. 5054. Egy \(\displaystyle M\) nyugalmi tömegű, kezdetben álló atommag képes elnyelni egy \(\displaystyle hf\) energiájú gamma-kvantumot. Határozzuk meg, hogy mekkora az atommag gerjesztési energiája (vagyis a nyugalmi energiájának növekedése) ebben a folyamatban!
Közli: Légrádi Imre, Sopron
(5 pont)
P. 5055. Egy vízszintesen kifeszített gumikötél egyik végét függőleges irányban periodikusan mozgatjuk, emiatt a kötél mentén transzverzális hullámok futnak végig. A kötél egy kis darabjának mozgásáról filmfelvételt készítünk, ennek három egymást követő filmkockáját mutatja az ábra.
Merre terjed a kötélben az energia: balról jobbra, vagy jobbról balra?
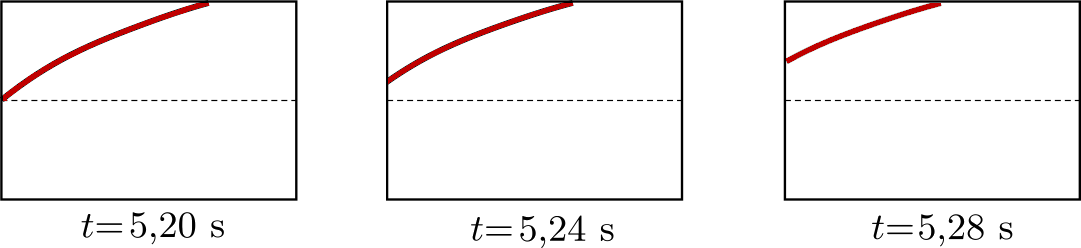
Közli: Gnädig Péter, Vácduka
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

