A KöMaL 2018. októberi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2018. november 12-én LEJÁRT. |
M. 380. Mérjük meg egy főtt tojás tehetetlenségi nyomatékát a szimmetriatengelyére vonatkozólag!
Közli: Simon Péter, Pécs
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2018. november 12-én LEJÁRT. |
G. 645. A NASA vákuumkamrájában filmre vették, ahogyan a kalapács és a madártoll is egyformán, \(\displaystyle g=9{,}81~\rm m/s^2\) gyorsulással esik a föld felé, egyszerre indítva őket egyszerre érnek talajt. Ha a filmet kétszeres sebességgel vetítik, mekkora lesz az így lejátszott moziban a kalapács és a toll gyorsulása?
(3 pont)
G. 646. Egy kémiaszertárban egyforma üvegekben tárolják a vegyszereket. Az egyik üveg tele van glicerinnel, a másik éterrel. A glicerines üveg tömege 2290 gramm, az éteresé 1471 gramm. Mekkora az üres üveg tömege?
(3 pont)
G. 647. Két – látszólag egyforma – vízforraló kancsóban szabályos hatszögben meghajlított fűtőszálat találunk. Az egyik kancsóban az \(\displaystyle a)\) ábra, a másikban a \(\displaystyle b)\) ábra szerint kötötték be a fűtőszálat. Melyik kancsóban forr fel hamarabb a víz?
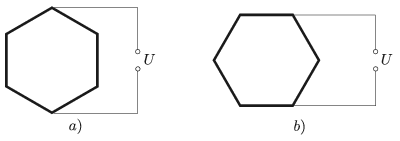
(3 pont)
G. 648. Egy kis bogár indul el egy 10 cm oldalélű fakocka \(\displaystyle P\) csúcsából. Legalább mennyi időre van szüksége a bogárnak ahhoz, hogy elérjen a kocka legtávolabbi \(\displaystyle Q\) csúcsához, ha a bogár sebessége 1 cm/s? Hányféle úton mozoghat a bogár, hogy a legrövidebb idő alatt odaérjen?
(4 pont)
 |
P-jelű feladatokA beküldési határidő 2018. november 12-én LEJÁRT. |
P. 5056. Egy 40 N/m rugóállandójú, elhanyagolható tömegű rugó függőleges helyzetben áll az asztalon. A rugó tetejéhez erősített, ugyancsak elhanyagolható tömegű lemezre egy 0,2 kg tömegű, kis méretű testet ejtünk, a lemeztől mérve 0,4 m magasságból. Mennyi ideig lesz a kis test a lemezen, ha nem tapad hozzá?
Közli: Kobzos Ferenc, Dunaújváros
(5 pont)
P. 5057. Egy \(\displaystyle \alpha=30^\circ\) hajlásszögű lejtőre helyezünk egy \(\displaystyle m=0{,}5\) kg tömegű és egy \(\displaystyle 3m\) tömegű kicsiny testet, amelyek elhanyagolható tömegű, \(\displaystyle d=50\) cm hosszúságú, merev rúddal vannak összekapcsolva. A lejtő felső része súrlódásmentes, az alsó részén a súrlódási együttható \(\displaystyle \mu=0{,}2\).
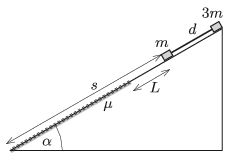
Kezdetben az \(\displaystyle m\) tömegű test \(\displaystyle L=40\) cm távolságra van attól a határvonaltól, ahol már van súrlódás, és \(\displaystyle s=120\) cm távol van a lejtő aljától. A két (pontszerűnek tekinthető) testből álló rendszert magára hagyjuk.
\(\displaystyle a)\) Adjuk meg a rúdban ébredő erőt a megtett út függvényében!
\(\displaystyle b)\) Mennyi idő alatt ér le az \(\displaystyle m\) tömegű test a lejtő aljára?
Közli: Kotek László, Pécs
(5 pont)
P. 5058. Egy hóbortos alaszkai vállalkozó különleges kalandparkot működtet. Egy nagyon magas jéghegy belsejében csavarvonal alakú bobpályát épít. A csavarvonal tengelye függőleges, átmérője \(\displaystyle d\), menetemelkedése \(\displaystyle h\). A pálya a hegy tetejétől indul, és a hegy aljánál egy rövid, súrlódásmentesnek tekinthető kanyar után \(\displaystyle s\) hosszúságú, vízszintes, egyenes szakaszban végződik. A pálya nagyon hosszú (az utasok számára ,,végtelen hosszúnak'' tűnik), és a bobok (amelyeken sem kormány, sem fék nincsen) éppen a vízszintes szakasz végén állnak meg. (Az egyszerűség kedvéért tekintsük a bobokat tömegpontoknak.)
\(\displaystyle a)\) Mekkora a csúszási súrlódási együttható a bob fémteste és a jég között?
\(\displaystyle b)\) Mekkora a bobok legnagyobb sebessége?
Adatok: \(\displaystyle d=10\) m, \(\displaystyle h=1{,}5\) m, \(\displaystyle s=270\) m.
Közli: Gnädig Péter, Vácduka
(5 pont)
P. 5059. Mennyi idő alatt esik be egy test a Napba, ha a Naptól 50 CSE távolságból, kezdősebesség nélkül indul? Mennyi idő alatt teszi meg a pályája felét?
Némedi István (1932–1998) feladata nyomán
(5 pont)
P. 5060. Két egyforma üvegballont keskeny, rövid cső köt össze, melynek belső térfogata elhanyagolható. A bennük lévő levegő hőmérséklete \(\displaystyle 27~{}^\circ\)C. Hány százalékkal nő a levegő nyomása a ballonokban, ha az egyik ballont \(\displaystyle 177~{}^\circ\)C-ra melegítjük, miközben a másikat \(\displaystyle 27~{}^\circ\)C-on tartjuk?
Példatári feladat nyomán
(4 pont)
P. 5061. Egy állandó tömegű ideális gázzal végzett folyamat egyenlete: \(\displaystyle pV^n= \text{állandó}\).
\(\displaystyle a)\) Mekkora \(\displaystyle n\) értéke, ha a folyamat izotermikus, izobár, vagy adiabatikus?
\(\displaystyle b)\) Mekkora lehet \(\displaystyle n\) értéke levegő esetén, ha a folyamat közben a gáz hőt ad le, és mégis felmelegszik?
Közli: Radnai Gyula, Budapest
(4 pont)
P. 5062. Kísérletek alapján tudjuk, hogy a vezetők ellenállása függ a hőmérséklettől. Egyes ötvözetek esetén az ellenállás hőfoktényezője negatív, míg mások esetében pozitív. Ennek felhasználásával különböző ötvözetekből készült vezetékek összekapcsolásával olyan huzalellenállásokat gyárthatunk, amelyek ellenállása széles tartományban független a hőmérséklettől. Az alábbi táblázatban konstantán és manganin esetében adtuk meg a vezeték egységnyi hosszára vonatkoztatott, \(\displaystyle 0~{}^\circ\)C-on mért ellenállásértékeket \(\displaystyle (r)\) és az ötvözeteket jellemző hőfoktényezőket (\(\displaystyle \alpha\)):
| \(\displaystyle r\;[\Omega/\rm m]\) | \(\displaystyle \alpha\;[1/{}^\circ\rm C]\) | |
| konstantán | 6,3 | \(\displaystyle -5{,}0\cdot 10^{-5}\) |
| manganin | 5,3 | \(\displaystyle +1{,}4\cdot 10^{-5}\) |
Milyen hosszúságú konstantánból és manganinból készült vezetékdarabokat kell sorba kötnünk ahhoz, hogy hőmérséklet-független, \(\displaystyle 5{,}0~\Omega\)-os ellenálláshoz jussunk?
Tornyai Sándor fizikaverseny, Hódmezővásárhely
(3 pont)
P. 5063. Az ábra szerinti kapcsolásban ideálisnak tekinthető műszerek vannak, amelyek a feltüntetett értékeket mutatják. Mekkorák az \(\displaystyle R_1\), \(\displaystyle R_2\), \(\displaystyle R_3\) és \(\displaystyle R_4\) ellenállások?
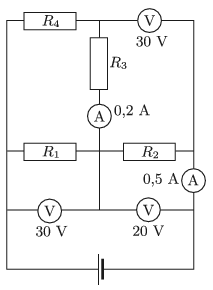
Közli: Zsigri Ferenc, Budapest
(4 pont)
P. 5064. Az ábrán látható, súrlódásmentesen tengelyezett, \(\displaystyle R=20\) cm sugarú, \(\displaystyle m_1=0{,}2\) kg tömegű, tömör szigetelőkorong peremére \(\displaystyle m_2=0{,}05\) kg tömegű rézgyűrűt erősítettünk, amelynek \(\displaystyle Q=8\cdot10^{-6}\) C töltést adtunk. A korong tengelyére rögzített, \(\displaystyle r=5\) cm sugarú csigára tekert vékony fonálon egy \(\displaystyle M=10\) kg tömegű nehezék függ, amelyet egy adott pillanatban lökésmentesen elengedünk. Indítás után \(\displaystyle t=3\) s múlva mekkora lesz a korong keltette mágneses indukció a korong közepénél? (Az önindukció jelensége figyelmen kívül hagyható.)
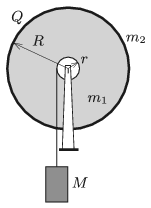
Közli: Holics László, Budapest
(5 pont)
P. 5065. Egy gömb alakú vízcseppre érkező fénysugár az ábrán látható módon, két belső visszaverődés után a bejövő sugárra merőleges irányban lép ki a vízcseppből. Mekkora a beesési szög? (A víz törésmutatója \(\displaystyle n=\frac43\).)
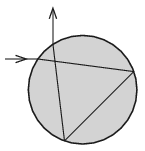
Közli: Cserti József, Budapest
(5 pont)
P. 5066. Egy átlátszó közegben \(\displaystyle z\) irányban változik az optikai törésmutató. Erre merőlegesen, az \(\displaystyle x\) tengely irányában vékony fénysugarat indítunk, amely a közegben a pozitív \(\displaystyle z\) irányba eltérülve parabolaív mentén halad. A törésmutató értéke \(\displaystyle z=0\)-nál \(\displaystyle n_0\), míg \(\displaystyle z=h\)-nál \(\displaystyle \sqrt{2}\,n_0\). Hogyan függ a törésmutató \(\displaystyle z\)-től?
Közli: Vigh Máté, Budapest
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

