A KöMaL 2019. februári matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2019. március 11-én LEJÁRT. |
K. 614. Keressük meg a 225. olyan számot a pozitív egész számok 1-től kezdődő növekvő sorozatában, amelyik nem írható fel két egymást követő egész szám szorzataként.
(6 pont)
K. 615. Egy négyzet belsejében helyezzünk el hat pontot úgy, hogy a négyzet csúcsai és a hat pont közül semelyik három ne essen egy egyenesre. Kössük össze ezt a tíz pontot (a négyzet csúcsait és a belső hat pontot) egymást nem metsző szakaszokkal. Ezt az összekötést addig folytassuk, amíg van két olyan pont a tíz közül, amit a fenti módon össze lehet kötni. Legfeljebb hány szakaszt lehet berajzolni így?
(6 pont)
K. 616. Sok egész számot fel lehet írni három egész szám négyzetének összegeként. Például: \(\displaystyle 1=1^2+0^2+0^2\), \(\displaystyle 14=3^2+2^2+1^2\), \(\displaystyle 20=4^2+2^2+0^2\). Mutassuk meg, hogy az 1991 nem írható fel három egész szám négyzetének összegeként.
(6 pont)
K. 617. Egy \(\displaystyle ABCDEFGH\) téglatest \(\displaystyle AG\) testátlója a \(\displaystyle BDE\) háromszöget a \(\displaystyle Q\) pontban metszi. Igazoljuk, hogy \(\displaystyle Q\) a \(\displaystyle BDE\) háromszög súlypontja.
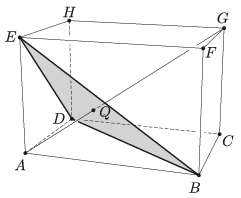
(6 pont)
K. 618. Egy pozitív egész számot nevezzünk ,,erős'' számnak, ha több osztója van, mint minden nála kisebb pozitív egész számnak. (Például a 2 erős szám, mert 2 osztója van, míg az 1-nek csak 1, de a 3 nem erős szám, mert 2 osztója van, ugyanúgy, mint a nála kisebb 2-nek.)
\(\displaystyle a)\) Adjuk meg a 2-nél nagyobb, de 30-nál kisebb erős számokat.
\(\displaystyle b)\) Erős szám-e a \(\displaystyle 2^3\cdot3^4\cdot5\)?
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2019. március 11-én LEJÁRT. |
C. 1525. Egy labdarúgó-bajnokságban 15 forduló után az egyik csapatnak 33 pontja volt. Addigi mérkőzései során előfordult döntetlen eredmény és vereség is. Hányszor győzött a csapat? (Győzelemért 3, vereségért 0, döntetlen esetén pedig mindkét csapatnak 1-1 pont jár.)
(5 pont)
C. 1526. Egy négyzet körülírt körének az oldalakra vett tükörképeit a négyzet belsejében érintő kör területét jelölje \(\displaystyle T\). Egy tükörképet és a körülírt kört is belülről érintő kör területét jelölje \(\displaystyle t\). Határozzuk meg \(\displaystyle \frac{T}{t}\) lehetséges legkisebb értékét.
(5 pont)
C. 1527. Az \(\displaystyle 1, 2, \dots, n\) számokból kettőt kitörölve a megmaradt számok összege 2019. Adjuk meg az összes lehetséges számpárt, amit kitörölhettünk.
(5 pont)
C. 1528. Milyen pozitív egész számot jelölhet \(\displaystyle n\), ha tudjuk, hogy az \(\displaystyle n^3\) szám utolsó három számjegyét letörölve az \(\displaystyle n\) számot kapjuk vissza?
Javasolta: Róka Sándor (Nyíregyháza)
(5 pont)
C. 1529. Bizonyítsuk be, hogy bármely derékszögű háromszög felbontható \(\displaystyle 3k+2\) darab egyenlőszárú háromszögre tetszőleges \(\displaystyle k\) pozitív egész szám esetén.
(5 pont)
C. 1530. Be lehet-e osztani 1-től 51-ig az egész számokat hármas csoportokba úgy, hogy minden csoportban a számok összege prím legyen?
(5 pont)
C. 1531. Egy szabályos háromoldalú egyenes hasáb térfogata \(\displaystyle 2~\textrm{dm}^3\). Legalább mekkora a hasáb felszíne?
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2019. március 11-én LEJÁRT. |
B. 5006. Az \(\displaystyle ABCD\) trapéz alapjai \(\displaystyle AB\) és \(\displaystyle CD\), az átlók metszéspontja \(\displaystyle M\). Az \(\displaystyle AC\) átló felezi a \(\displaystyle BAD\) szöget, \(\displaystyle AM=BC\) és \(\displaystyle BM=CD\). Határozzuk meg a trapéz szögeit.
OKTV feladat alapján
(4 pont)
B. 5007. Van \(\displaystyle 3n+1\) darab érménk. Ezek közül \(\displaystyle n\) érmének az egyik oldalán 0, a másik oldalán \(\displaystyle 11\) áll. További \(\displaystyle n\) érmének az egyik oldalán 0, a másik oldalán \(\displaystyle 44\), a többi \(\displaystyle n+1\) érmének pedig az egyik oldalán 0, a másik oldalán \(\displaystyle 99\) szerepel. Az összes érmét egyszerre feldobva mi annak a valószínűsége, hogy a dobott számok összege 7-tel osztható? (Az érmék mindkét oldalukra azonos eséllyel esnek.)
(4 pont)
B. 5008. Adottak az \(\displaystyle A\) középpontú \(\displaystyle k_A\) és a \(\displaystyle B\) középpontú \(\displaystyle k_B\) körök. Az \(\displaystyle l_1\) egyenes \(\displaystyle A_1\)-ben érinti \(\displaystyle k_A\)-t és \(\displaystyle B_1\)-ben \(\displaystyle k_B\)-t; az \(\displaystyle l_2\) egyenes pedig \(\displaystyle A_2\)-ben érinti \(\displaystyle k_A\)-t és \(\displaystyle B_2\)-ben \(\displaystyle k_B\)-t. Bizonyítsuk be, hogy az \(\displaystyle A_1A_2\) és a \(\displaystyle B_1B_2\) szakaszok \(\displaystyle AB\) egyenesre vett merőleges vetülete egyenlő hosszúságú.
(3 pont)
B. 5009. Az \(\displaystyle x\), \(\displaystyle y\), \(\displaystyle z\) pozitív számokra \(\displaystyle x^2+y^2+z^2=3\) teljesül. Bizonyítsuk be, hogy \(\displaystyle 2^{\tfrac1x} + 2^{\tfrac1y} + 2^{\tfrac1z} \ge 6\).
Javasolta: Nguyen Van Nho (Vietnam)
(3 pont)
B. 5010. Egy hegyesszögű \(\displaystyle ABC\) háromszög beírt köre az oldalakat az \(\displaystyle A_0\), \(\displaystyle B_0\) és \(\displaystyle C_0\) pontokban érinti. A háromszög három hozzáírt körének érintési pontjai az oldalegyeneseken rendre \(\displaystyle A_1\), \(\displaystyle B_1\) és \(\displaystyle C_1\); \(\displaystyle A_2\), \(\displaystyle B_2\) és \(\displaystyle C_2\); illetve \(\displaystyle A_3\), \(\displaystyle B_3\) és \(\displaystyle C_3\). Az \(\displaystyle A_iB_iC_i\) háromszög területét jelölje \(\displaystyle T_i\) (\(\displaystyle i=0,1,2,3\)). Mutassuk meg, hogy
\(\displaystyle \frac{1}{T_0}=\frac{1}{T_1}+\frac{1}{T_2}+\frac{1}{T_3}. \)
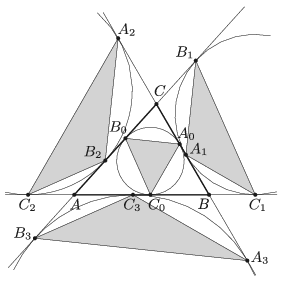
(5 pont)
B. 5011. Adott a síkon 6 általános helyzetű pont úgy, hogy bármely két pont távolsága különböző. Mutassuk meg, hogy megadható két olyan háromszög, amelyeknek minden csúcsa ezen pontok közül való, és a két háromszögnek van egy közös oldala, amely az egyik háromszögben a legrövidebb, a másikban a leghosszabb oldal.
Javasolta: Róka Sándor (Nyíregyháza)
(5 pont)
B. 5012. Legyen \(\displaystyle f(x)\) egész együtthatós polinom. Jelölje \(\displaystyle f^{(n)}\) az \(\displaystyle f\) függvény \(\displaystyle n\)-szeri alkalmazását:
\(\displaystyle f^{(n)}(x)=\underbrace{f\Big(f\big(\ldots f}_{n}(x)\ldots\big)\!\Big). \)
Jelölje \(\displaystyle k(f)\) a legkisebb olyan \(\displaystyle k\) pozitív egészt, melyre \(\displaystyle f^{(k)}(x)\equiv x\pmod{13}\) teljesül minden \(\displaystyle x\) egész számra, ha létezik ilyen \(\displaystyle k\), és legyen \(\displaystyle k(f)=0\) egyébként. Mutassuk meg, hogy a \(\displaystyle k(f)\) értékek között létezik legnagyobb, és határozzuk meg a maximumot.
(6 pont)
B. 5013. Az \(\displaystyle ABC\) háromszög \(\displaystyle A\)-val szemközti hozzáírt köre az \(\displaystyle AC\) egyenest a \(\displaystyle B_1\) pontban érinti, a \(\displaystyle BB_1\) szakasz a hozzáírt kört \(\displaystyle B_2\)-ben metszi, és a hozzáírt körhöz \(\displaystyle B_2\)-ben húzott érintő a \(\displaystyle BC\) oldalt \(\displaystyle B_3\)-ban metszi. Hasonlóan, a háromszög beírt köre az \(\displaystyle AB\) oldalt a \(\displaystyle C_1\) pontban érinti, a \(\displaystyle CC_1\) szakasz a beírt kört \(\displaystyle C_2\)-ben metszi, és a beírt körhöz \(\displaystyle C_2\)-ben húzott érintő a \(\displaystyle BC\) oldalt a \(\displaystyle C_3\) pontban metszi. Mutassuk meg, hogy \(\displaystyle B_2B_3=C_2C_3\).
(6 pont)
 |
A-jelű feladatokA beküldési határidő 2019. március 11-én LEJÁRT. |
A. 743. Az \(\displaystyle ABCD\) konvex érintőnégyszög beírt köre a \(\displaystyle BD\) átlót a \(\displaystyle P\) és \(\displaystyle Q\) pontokban metszi (\(\displaystyle BP<BQ\)). A beírt kör \(\displaystyle AC\)-re merőleges átmérője \(\displaystyle UV\) (\(\displaystyle {BU<BV}\)). Mutassuk meg, hogy az \(\displaystyle AC\), \(\displaystyle PV\) és \(\displaystyle QU\) egyenesek egy ponton mennek át.
IOM 2018 (Moszkva) 2. feladata alapján
(7 pont)
A. 744. Mutassuk meg, hogy bármely páratlan \(\displaystyle N>5\) egész számhoz léteznek olyan \(\displaystyle \mathbf{u}\), \(\displaystyle \mathbf{v}\), \(\displaystyle \mathbf{w}\) vektorok a (három dimenziós) térben, amelyek páronként merőlegesek egymásra, nem párhuzamosak egyik koordináta-tengellyel sem, a koordinátáik egész számok, és \(\displaystyle |\mathbf{u}|=|\mathbf{v}|=|\mathbf{w}|=N\).
A 2018. évi Kürschák-verseny 2. feladata alapján
(7 pont)
A. 745. Egy konvex poliéder minden lapja egy óramutatót hordoz; a mutatók mindig valamelyik élben szomszédos lap felé mutatnak. Minden perc végén valamelyik lap mutatója – az órajárás szerinti irányban – elfordul a következő lap felé úgy, hogy szomszédos lapok mutatói soha nem mutatnak egymás felé. Mutassuk meg, hogy van olyan mutató, amely csak véges sokszor fordul el.
(7 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

