A KöMaL 2019. májusi matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
C-jelű feladatokA beküldési határidő 2019. június 11-én LEJÁRT. |
C. 1546. Oldjuk meg az egész számpárok halmazán a következő egyenletet:
\(\displaystyle (x-8)(x-10)=2^y. \)
(Amerikai versenyfeladat)
(5 pont)
C. 1547. Az \(\displaystyle ABCDEF\) szabályos hatszög \(\displaystyle EF\) oldalának felezőpontját jelölje \(\displaystyle K\). Adjuk meg az \(\displaystyle ABCD\) töröttvonalon azt az \(\displaystyle L\) pontot, melyre az \(\displaystyle AKL\) háromszög területe egyenlő a hatszög területének \(\displaystyle \frac25\) részével.
Bakos Tibor feladata nyomán
(5 pont)
C. 1548. Anna gondol egy \(\displaystyle 3\times 3\)-as négyzet néhány mezőjére. Ezután megmondja Bálintnak minden sorról és oszlopról, hogy hány mező szerepel benne az általa gondoltak közül. Hányféleképpen tud Anna úgy gondolni, hogy az általa adott információkból Bálint ne találhassa ki egyértelműen, melyek voltak a gondolt mezők?
(5 pont)
C. 1549. Az \(\displaystyle AB\) szakasz felezőpontja legyen \(\displaystyle F\), továbbá legyen az \(\displaystyle AF\) szakasz egy tetszőleges pontja \(\displaystyle Z\). \(\displaystyle F\)-ben merőlegest állítunk \(\displaystyle AB\)-re és felmérjük rá az \(\displaystyle {FX=FA}\) távolságot. \(\displaystyle B\)-ben is merőlegest állítunk \(\displaystyle AB\)-re és felmérjük rá a \(\displaystyle BY=AZ\) távolságot úgy, hogy \(\displaystyle X\) és \(\displaystyle Y\) az \(\displaystyle AB\) egyenesének egyazon oldalán legyenek. Mekkora lehet az \(\displaystyle XZY\) szög?
Javasolta: Surányi László (Budapest)
(5 pont)
C. 1550. Oldjuk meg az
\(\displaystyle n\cdot(1!+2!+3!+\ldots+n!)=(n+1)! \)
egyenletet a pozitív egész számok halmazán.
(5 pont)
C. 1551. Adott az \(\displaystyle ABC\) háromszög, melyről a következőket tudjuk: \(\displaystyle AD\) és \(\displaystyle BE\) súlyvonalának hossza 3 cm, illetve 6 cm, a háromszög területe pedig \(\displaystyle 3\sqrt{15}\,~\mathrm{cm}^2\). Határozzuk meg a harmadik súlyvonal hosszát, ha tudjuk, hogy ez a másik kettőtől különbözik.
(5 pont)
C. 1552. Bizonyítsuk be, hogy ha \(\displaystyle 0<a<1\) és \(\displaystyle 0<b<1\), akkor
\(\displaystyle \log_a\frac{2ab}{a+b}\cdot\log_b\frac{2ab}{a+b}\ge 1. \)
Javasolta: Róka Sándor (Nyíregyháza)
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2019. június 11-én LEJÁRT. |
B. 5030. Mutassuk meg, hogy minden \(\displaystyle 1\)-nél nagyobb egész felírható \(\displaystyle 1\)-nél nagyobb, \(\displaystyle 2^p\cdot 3^q\) alakú számok összegeként úgy, hogy az összegnek nincs két olyan tagja, melyek egyike a másiknak osztója. (Például \(\displaystyle 23=9+8+6\), \(\displaystyle 11=9+2\) vagy \(\displaystyle 12=12\).)
Erdős Pál feladata
(4 pont)
B. 5031. Az \(\displaystyle ABCD\) paralelogramma \(\displaystyle AD\) oldalának \(\displaystyle D\)-n túli meghosszabbításán vegyük fel az \(\displaystyle F\) pontot. A \(\displaystyle BF\) szakasz a \(\displaystyle CD\) oldalt a \(\displaystyle G\), az \(\displaystyle AC\) átlót pedig az \(\displaystyle E\) pontban metszi. Mutassuk meg, hogy
\(\displaystyle \frac{1}{BE}=\frac{1}{BG}+\frac{1}{BF}. \)
(3 pont)
B. 5032. Mi a mértani helye egy egyenlő szárú háromszög belsejében azoknak a pontoknak, amelyeknek a száraktól mért távolságaik mértani közepe az alaptól mért távolsággal egyenlő?
(4 pont)
B. 5033. Az \(\displaystyle \binom{n+1}{2}\) darab \(\displaystyle a_{1,1}, a_{1,2}, \ldots, a_{1,n}, a_{2,1}, a_{2,2}, \ldots, a_{2,n-1}, \ldots, a_{k,1}, \ldots, a_{k,n+1-k}, \ldots, a_{n,1}\) számot \(\displaystyle n\)-edrendű fordított Pascal-piramisnak hívjuk, ha tetszőleges \(\displaystyle 2 \le k \le n\) és \(\displaystyle 1 \le j \le n+1-k\) esetén \(\displaystyle a_{k,j}=a_{k-1,j} + a_{k-1,j+1}\). Egy példa 3-adrendű fordított Pascal-piramisra:
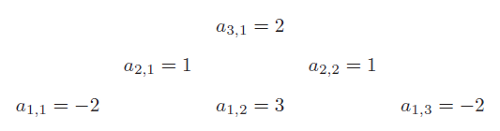
Jelentse \(\displaystyle s_k\) a piramis \(\displaystyle k\)-adik sorában lévő számok összegét, azaz \(\displaystyle s_k = a_{k,1} + a_{k,2} + \ldots + a_{k,n+1-k}\). Egy piramis jelváltó a \(\displaystyle k\)-adik (\(\displaystyle k>1\)) sorában, ha \(\displaystyle s_{k-1} \cdot s_k <0\). Adott \(\displaystyle n\) esetén legfeljebb mekkora lehet a \(\displaystyle k\) értéke, ha egy \(\displaystyle n\)-edrendű piramis jelváltó a \(\displaystyle 2., 3., \ldots, k\)-adik sorában, de a \(\displaystyle (k+1)\)-edik sorában már nem? (A fenti példában \(\displaystyle k=2\), mert \(\displaystyle s_1 \cdot s_2 = -2 <0\), de már \(\displaystyle s_2 \cdot s_3 = 4 >0\).)
(5 pont)
B. 5034. Bizonyítandó, hogy ha egy konvex négyszög szögei \(\displaystyle \alpha\), \(\displaystyle \beta\), \(\displaystyle \gamma\), \(\displaystyle \delta\), és egyik sem derékszög, akkor
\(\displaystyle \tg \alpha+\tg \beta+\tg \gamma+\tg \delta=\tg \alpha\cdot\tg \beta\cdot\tg \gamma\cdot \tg \delta(\ctg \alpha+\ctg\beta+\ctg\gamma+\ctg\delta). \)
Surányi János feladata
(3 pont)
B. 5035. Bizonyítsuk be, hogy ha az \(\displaystyle n\ge 8\) csúcsú teljes gráf éleit kiszínezzük két színnel, akkor több, mint \(\displaystyle \frac{{(n-5)}^4}{64}\) egyszínű, négy hosszú kör keletkezik.
Pálfy Máté (Budapest) javaslata nyomán
(6 pont)
B. 5036. Az \(\displaystyle M\) pontból két érintőt húztunk egy \(\displaystyle O\) középpontú derékszögű hiperbolához. Az egyik érintő a hiperbola egyik aszimptotáját a \(\displaystyle P\), a másik érintő a másik aszimptotát a \(\displaystyle Q\) pontban metszi. Igazoljuk, hogy az \(\displaystyle OM\) egyenes felezi a \(\displaystyle PQ\) szakaszt.
(5 pont)
B. 5037. Adott egy \(\displaystyle P\) poliéder. A \(\displaystyle P\)-t feldaraboljuk a \(\displaystyle P_1, \ldots, P_k\) poliéderekre, valamint a \(\displaystyle Q_1, \ldots, Q_k\) poliéderekre is úgy, hogy minden \(\displaystyle i=1, \ldots, k\) esetén a \(\displaystyle P_i\) és \(\displaystyle Q_i\) poliéderek egybevágóak. Mutassuk meg, hogy kijelölhetünk \(\displaystyle P\) belsejében néhány pontot úgy, hogy minden \(\displaystyle i=1, \ldots, k\) esetén a \(\displaystyle P_i\) és \(\displaystyle Q_i\) poliéderek belsejébe ugyanannyi (legalább egy) pont esik. (Minden poliéder helyzete rögzített a térben.)
(6 pont)
 |
A-jelű feladatokA beküldési határidő 2019. június 11-én LEJÁRT. |
A. 752. Legyenek \(\displaystyle k\), \(\displaystyle s\) és \(\displaystyle n\) pozitív egész számok úgy, hogy \(\displaystyle s<(2k+1)^2\), és legyen \(\displaystyle R\) a sík azon \(\displaystyle (x,y)\) rácspontjainak halmaza, amelyre \(\displaystyle 1\le x,y\le n\). Az \(\displaystyle R\) pontrácson a következő eljárást végezzük el. Kezdetben \(\displaystyle R\) egy pontját zöldre, a többi pontját fehérre színezzük. Ezután minden lépésben kiválasztunk egy \(\displaystyle {\color{red}(2k+1)\times(2k+1)}\) rácspontból álló \(\displaystyle S\) négyzetet, amelynek középpontja zöld, és legalább \(\displaystyle s\) fehér pontot tartalmaz, majd az \(\displaystyle S\)-beli fehér pontok közül valamelyik \(\displaystyle s\) pont színét zöldre változtatjuk. Ezt a lépést addig ismételgetjük, amíg csak található megfelelő \(\displaystyle S\) négyzet.
Azt mondjuk, hogy az \(\displaystyle s\) szám \(\displaystyle k\)-ritka, ha létezik olyan \(\displaystyle C\) pozitív valós szám, hogy bármely \(\displaystyle n\), bármely kiinduló zöld pont, és a fenti lépések bármely szabályos sorozata után a zöld pontok száma nem lehet nagyobb, mint \(\displaystyle Cn\).
Fejezzük ki a legkisebb \(\displaystyle k\)-ritka egész \(\displaystyle s\) számot \(\displaystyle k\) függvényében.
Javasolta: Nikolai Beluhov (Sztara Zagora, Bulgária)
(7 pont)
A. 753. Legyen \(\displaystyle a\) egész szám, és legyen \(\displaystyle p\) az \(\displaystyle a^3+a^2-4a+1\) egy prímosztója. Mutassuk meg, hogy van olyan \(\displaystyle b\) egész szám, amelyre \(\displaystyle p\equiv b^3\pmod{13}\).
(7 pont)
A. 754. Legyen \(\displaystyle P\) az \(\displaystyle ABC\) hegyesszögű háromszög belső pontja, és legyen \(\displaystyle Q\) a \(\displaystyle P\) izogonális konjugáltja. Legyen \(\displaystyle L\), \(\displaystyle M\) és \(\displaystyle N\) a körülírt kör rövidebbik \(\displaystyle BC\), \(\displaystyle CA\), illetve \(\displaystyle AB\) ívének felezőpontja. Legyen \(\displaystyle X_A\) az \(\displaystyle LQ\) félegyenes és a \(\displaystyle PBC\) kör metszéspontja, \(\displaystyle X_B\) az \(\displaystyle MQ\) félegyenes és a \(\displaystyle PCA\) kör metszéspontja, és \(\displaystyle X_C\) az \(\displaystyle NQ\) félegyenes és a \(\displaystyle PAB\) kör metszéspontja. Bizonyítsuk be, hogy a \(\displaystyle P\), \(\displaystyle X_A\), \(\displaystyle X_B\) és \(\displaystyle X_C\) pontok egy körön vannak vagy egybeesnek.
Javasolta: Gustavo Cruz (São Paulo)
(7 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

