A KöMaL 2020. szeptemberi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2020. október 15-én LEJÁRT. |
M. 397. Gyertyával bekormozott fémlemez hőmérsékletét mérve határozzuk meg, hogy mennyi energia érkezik a Napból egységnyi idő alatt a sugárzásra merőleges, egységnyi nagyságú felületre! (A fémlemez anyagának fajhőjét vegyük táblázatból.)
Közli: Tichy Géza, Budapest
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2020. október 15-én LEJÁRT. |
G. 713. Egy 80 kg tömegű fizikatanár 6 méter hosszú és 40 kg tömegű, erős pallóból olyan kétoldalú emelőt készít, amivel a diákjainak bemutatja, hogy akár egy 500 kg tömegű terhet is fel tud vele emelni. Hová helyezze az emelő alátámasztását, ha a terhet maximális magasságba akarja juttatni úgy, hogy teljes súlyával óvatosan ránehezedik a palló végére? A teher tömegközéppontján áthaladó függőleges egyenes 20 cm távol van a palló végétől.

(4 pont)
G. 714. A Föld jégsapkái és gleccserei jelenleg mintegy \(\displaystyle 30\,000\,000~\mathrm{km}^3\) jeget tartalmaznak. Becsüljük meg, hogy nagyjából mennyivel emelkedne a tengerek és az óceánok vízszintje, ha ez a hatalmas mennyiségű jég mind elolvadna!
(3 pont)
G. 715. Egy áramkör három ellenállásból és egy telepből áll az ábrán látható módon.
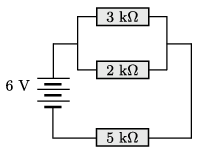
\(\displaystyle a)\) Mekkora az egyes ellenállásokon átfolyó áram és a rajtuk eső feszültség?
\(\displaystyle b)\) Hogyan változnak ezek az értékek, ha a két párhuzamos ellenállás mellé még bekötünk rengeteg (,,végtelen sok'') \(\displaystyle 1~\mathrm{k}\Omega\)-os ellenállást párhuzamosan?
\(\displaystyle c)\) Mekkora lesz az eredeti áramkör három ellenállásának árama és feszültsége, ha az \(\displaystyle 5~\mathrm{k}\Omega\)-os ellenállás mellé bekötünk még rengeteg (,,végtelen sok'') \(\displaystyle 1~\mathrm{k}\Omega\)-os ellenállást sorosan?
(A nyomtatásban megjelent feladat ábráján tévesen szerepelnek az ellenállások. Helyesen mindhárom ellenállás nagysága k\(\displaystyle \Omega\)-ként értendő.)
(4 pont)
G. 716. Egy ágyúból kilőtt gránát pályájának legfelső pontján 100 m/s sebességgel haladva két egyforma tömegű darabra robban szét. Az egyik darab 50 m/s sebességgel függőlegesen felfelé indul el. Milyen irányba és mekkora sebességgel indul el a másik darab? (A gránátban lévő robbanóanyag tömege elhanyagolható.)
(3 pont)
 |
P-jelű feladatokA beküldési határidő 2020. október 15-én LEJÁRT. |
P. 5240. Hány liter levegő szorul ki egy \(\displaystyle 6~{\mathrm{m}}\times 5~{\mathrm{m}}\times 3~{\mathrm{m}}\)-es helyiségből, ha a levegő hőmérséklete \(\displaystyle 27\;{}^\circ\)C-ról \(\displaystyle 30\;{}^\circ\)C-ra emelkedik, a nyomás pedig 0,5%-kal csökken?
Példatári feladat nyomán
(3 pont)
P. 5241. Az erős délnyugati szél hatására 1962. május 14-én 9 óra alatt 45 cm-rel csökkent Keszthelynél a Balaton vízszintje, amíg Alsóörsnél 51 cm-t emelkedett. Adjunk nagyságrendi becslést a szélnek a víz emelésére fordított teljesítményére! (Becslésünkhöz felhasználhatjuk az interneten elérhető adatokat is.)
Közli: Radnai Gyula, Budapest
(4 pont)
P. 5242. Egy felhőben 2 mm átmérőjű, gömb alakú esőcseppek lebegnek. Mekkora sebességgel áramlik felfelé az 1 kg/m\(\displaystyle {}^3\) sűrűségű levegő a felhőben? (A közegellenállási erő a sebesség négyzetével arányos.)
Közli: Honyek Gyula, Veresegyház
(4 pont)
P. 5243. Egy sportcsarnokban a kézilabdázók az indítást gyakorolják úgy, hogy a terem falával párhuzamosan futva a falhoz dobott labdát elkapják. Az egyik játékos a faltól 3 méterre, folyamatosan 5 m/s sebességgel szalad. A teremhez képest legalább mekkora sebességgel kell eldobnia a labdát ahhoz, hogy utána épp az eldobás magasságában tudja majd elkapni? A labda ütközését a fallal tekintsük tökéletesen rugalmasnak.
Közli: Kis Tamás, Heves
(5 pont)
P. 5244. Egy bizonyos fajta elemi részecske szilárd anyagban mozogva a megtett úttal arányosan veszít az energiájából, és valahol megáll. A \(\displaystyle v_0=10^7\) m/s kezdősebességű részecskék egy ritkább anyagba \(\displaystyle s_1=3\) cm, egy sűrűbb anyagba pedig \(\displaystyle s_2=2\) cm mélyen hatolnak be. Mekkora út megtétele után állnak meg az ugyanekkora kezdősebességű részecskék, ha a sűrűbb anyag \(\displaystyle d=1{,}5\) cm vastag rétegén áthatolva a ritkább anyagba érnek?
Közli: Gnädig Péter, Vácduka
(4 pont)
P. 5245. Teherszállító repülőgép halad az Egyenlítő felett 11 km magasan 1000 km/h sebességgel, először nyugati, majd keleti irányban. A repülőtéren hitelesített rugós mérleg segítségével mindkét alkalommal megmérik a gépben egy, a fedélzeten lévő nehéz tárgy tömegét. A két mért érték között 1 kg a különbség. Mekkora a tárgy valódi tömege?
Közli: Simon Péter, Pécs
(4 pont)
P. 5246. Hévízen, a tó aljának azon részén, ahol a tölcsér sziklafalából, a felszín alatt kiömlik a víz a tóba, a felkavart iszaprétegből induló, végig gömb alakúnak feltételezett légbuborék átmérője 50%-kal megnő, miközben az állandó hőmérsékletű víz felszínére érkezik. Mekkora a víz mélysége az iszapréteg felett?
Közli: Tornyos Tivadar Eörs, Budapest
(4 pont)
P. 5247. Egy téglatest alakú akvárium két szemközti oldalán egy-egy kör alakú nyílás van, melyeket vékony, kis nyílásszögű gömbsüvegek fednek (lásd az ábrát). A gömbsüvegek közös optikai tengelye vízszintes. A befelé domboruló gömbsüveg görbületi sugara \(\displaystyle r\), a kifelé domborulóé \(\displaystyle 2r\). A gömbsüvegek teteje alacsonyabban van, mint az akváriumban lévő, \(\displaystyle n=4/3\)-os törésmutatójú víz felszíne.
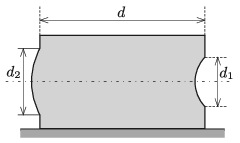
\(\displaystyle a)\) Mekkora \(\displaystyle d\) távolságra van egymástól az akvárium gömbsüvegeket tartalmazó két oldala, ha az egyik gömbsüvegre vízszintesen érkező, párhuzamos fénysugarak a másik gömbsüvegen át vízszintesen, párhuzamosan hagyják el az akváriumot?
\(\displaystyle b)\) Mekkora a két gömbsüveg \(\displaystyle d_2\), illetve \(\displaystyle d_1\) átmérőjének aránya, ha az akváriumba bármelyik gömbsüvegen át belépő, vízszintes fénynyaláb teljes egészében a másik gömbsüvegen lép ki?
\(\displaystyle c)\) Az optikai tengelyen, az akvárium közepén van egy piciny halacska. Hol látható ez az egyik, illetve a másik oldali gömbsüvegen át nézve?
Közli: Zsigri Ferenc, Budapest
(5 pont)
P. 5248. Egy \(\displaystyle 4\ell\) hosszúságú ellenálláshuzalt a két negyedelőpontjában derékszögben meghajlítottunk. Hol kell ehhez hozzákötni a \(\displaystyle 2\ell\) hosszúságú, ugyanebből a huzalból levágott vezetőt, ha azt akarjuk, hogy a huzalvégek között kialakuló eredő ellenállás megegyezzen egyetlen \(\displaystyle 2\ell\) hosszúságú vezető ellenállásával?

Példatári feladat nyomán
(4 pont)
P. 5249. Az AA jelű akkumulátor hossza 5 cm, átmérője 1,4 cm.
\(\displaystyle a)\) Mekkora energiát tárol egy 1,2 V-os, 2800 mAh-s akku?
\(\displaystyle b)\) Mekkora sebességre gyorsulna fel ez a 17 grammos akku, ha az eltárolt energiáját teljesen a saját mozgási energiájává alakítaná?
\(\displaystyle c)\) Hányszor kevesebb energiával lehetne ugyanekkora térfogatú vizet \(\displaystyle 20\;{}^\circ\)C-ról \(\displaystyle 100\;{}^\circ\)C-ra melegíteni?
\(\displaystyle d)\) Mennyi energia van ugyanekkora térfogatú kristálycukorban, amelynek sűrűsége kb. 0,77 g/cm\(\displaystyle {}^3\), energiatartalma pedig 1680 kJ/100 gramm?
Közli: Vass Miklós, Budapest
(4 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

