A KöMaL 2021. januári fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2021. február 18-án LEJÁRT. |
M. 401. Készítsünk egy \(\displaystyle m\) tömegű, \(\displaystyle \ell\) hosszúságú, homogén tömegeloszlású, az egyik végén tengelyezett, vékony lécből fizikai ingát. (\(\displaystyle m\) és \(\displaystyle \ell\) szabadon választható értékek, amelyeket a mérés során nem változtatunk.)
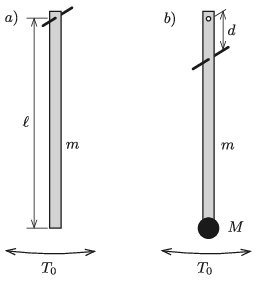
\(\displaystyle a)\) Mérjük meg a kissé kitérített inga \(\displaystyle T_0\) lengésidejét!
Ezután helyezzük át a forgástengelyt a léc egyik végétől \(\displaystyle d\) távolságra, és rögzítsünk a léc másik végére egy pontszerűnek tekinthető, \(\displaystyle M\) tömegű testet (például egy darab gyurmát). Ha megfelelően választjuk meg \(\displaystyle M\) nagyságát, akkor az így kapott fizikai inga lengésideje az eredeti \(\displaystyle T_0\)-lal egyezik meg.
\(\displaystyle b)\) Mérjük meg, hogyan függ a \(\displaystyle M/m\) tömegarány a \(\displaystyle d/\ell\) távolságaránytól!
Közli: Gnädig Péter, Vácduka
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2021. február 18-án LEJÁRT. |
G. 729. Ha az olvasztott zsírt egy edényben kihűlni hagyjuk, jól megfigyelhető, hogy a megfagyott zsír felülete kráterszerű lesz, a perem mentén szabályos karima képződik. Miért?
(3 pont)
G. 730. Egy kerékpáros versenyen az első és a második helyen állók állandó \(\displaystyle v_0 = 50\) km/h nagyságú sebességgel haladnak. Az elsőnek \(\displaystyle d = 100\) m előnye van. Egy adott pillanatban – már a cél közelében – a harmadik helyen álló rákapcsol, \(\displaystyle v_1 = 55\) km/h nagyságú sebességgel megelőzi a másodikat, és ezt a sebességet tartani is tudja. Az előzés helyétől milyen messze lehet a cél, ha az első helyen álló versenyző megnyeri a versenyt?
(4 pont)
G. 731. Egy kertvárosi övezetben, ahol 30 km/h a megengedett legnagyobb sebesség, egy autó – kicsit szabálytalanul – 36 km/h sebességgel halad. Megelőzi őt egy másik, ugyanolyan autó 54 km/h sebességgel. Éppen egymás mellett haladnak, amikor 20 méternyire előttük egy gyerek kiszalad az úttestre. A két autó sofőrje egyszerre kezd el ugyanolyan erősen fékezni.
\(\displaystyle a)\) Mekkora ,,megmaradó'' sebességgel halad el a gyerek mellett a gyorsabb autó, ha a lassabb autó éppen megáll a gyerek előtt?
\(\displaystyle b)\) Hogyan változik az eredmény, ha figyelembe vesszük azt is, hogy mindkét sofőr reakcióideje kb. 1 másodperc?
Közli: Csapodi Csaba, Budapest
(4 pont)
G. 732. Újsághír (2020. november 17.): ,,Megérkezett a Nemzetközi Űrállomásra (ISS) a Crew Dragon űrhajó! 27 órás, teljesen automatizált repülést követően dokkolt a Föld felett körülbelül 400 kilométerrel lebegő űrállomáson.'' Adjunk becslést a következőkre:
\(\displaystyle a)\) Hányszor kerülte meg ez az űrhajó a Földet az elindulástól a dokkolásig?
\(\displaystyle b)\) Mekkora volt a ,,lebegő'' űrállomás keringési sebessége dokkoláskor?
(4 pont)
 |
P-jelű feladatokA beküldési határidő 2021. február 18-án LEJÁRT. |
P. 5283. A ,,Kihívás Napján'' rendezett iskolai futóversenyre három barát, Sebi, Tóni és Zoli is benevezett. A 2,4 km-es távot mindhárman egyenletesen futották végig. Amikor Tóni épp a táv 68%-ánál járt, akkor Sebire még 3 percnyi futás várt. Zoli futása során Sebinél 20 cm-rel több, Tóninál viszont 1 dm-rel kevesebb utat tett meg másodpercenként.
\(\displaystyle a)\) Mennyi idő telt el Zoli és Tóni célba érkezése között?
\(\displaystyle b)\) Hány méterre volt Sebi a céltól, amikor Tóni beért?
Közli: Kis Tamás, Heves
(4 pont)
P. 5284. Egy alkoholos fertőtlenítő oldat flakonján ezt olvassuk: ,,Hatóanyag: etil-alkohol (70 V/V%)''. Egy másik hatóanyaga 67,9 m/m%-os etanol (etil-alkohol) oldat. Feltételezve, hogy az egyéb adalékanyagok mennyisége elhanyagolható, melyik készítményben nagyobb az alkohol koncentrációja? (Az etanol–víz elegy sűrűsége a koncentráció függvényében megtalálható a Négyjegyű függvénytáblázat kémia részében.) Adjunk általánosan alkalmazható összefüggést az oldat térfogat- és tömegszázalékban kifejezett töménysége és a sűrűsége között!
Közli: Woynarovich Ferenc, Budapest
(4 pont)
P. 5285. Lapos, korong alakú, \(\displaystyle m\) tömegű test vízszintes, érdes felületen nyugszik. Egy \(\displaystyle D\) direkciós erejű rugó egyik végét a korong közepéhez erősítjük, majd a másik végét vízszintes irányban lassan húzni kezdjük. Kezdetben a rugó feszítetlen. A test egy ideig mozdulatlan, majd megindul, és egyenes vonalban mozog. A korong megindulásának pillanatában a rugó másik végét rögzítjük.
\(\displaystyle a)\) Mekkora lesz a test maximális sebessége?
\(\displaystyle b)\) Mennyi idő alatt éri el a maximális sebességet?
\(\displaystyle c)\) Mekkora távolságot tesz meg a korong a maximális sebesség eléréséig?
\(\displaystyle d)\) Hogyan mozog a korong a továbbiakban, feltételezve, hogy a rugó mindig egyenes marad?
A korong és az érdes felület között a csúszási súrlódási együttható \(\displaystyle \mu\), a tapadási súrlódás együtthatója pedig \(\displaystyle \mu_0\) (\(\displaystyle \mu_0>\mu\)).
Közli: Wiedemann László, Budapest
(5 pont)
P. 5286. Egy \(\displaystyle R\) sugarú, homogén tömegeloszlású, \(\displaystyle \varphi\) szöggel ,,hiányos'' vékony hengerpalástot vízszintes asztalra fektetünk az ábrán látható módon. A hengerpalástot kissé kimozdítjuk egyensúlyi helyzetéből, majd elengedjük. Határozzuk meg a hengerpalást rezgőmozgásának periódusidejét! Feltételezhetjük, hogy súrlódás elegendően nagy, így a hengerpalást a rezgőmozgás közben nem csúszik meg.
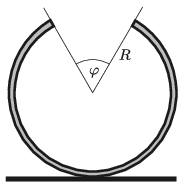
Adatok: \(\displaystyle R= 0{,}2\) m; \(\displaystyle \varphi=\pi/3\).
Közli: Takács Árpád, Budapesti Berzsenyi D. Gimn.
(5 pont)
P. 5287. Van három ellenállásunk, rendre 1 ohm, 2 ohm, 3 ohm értékűek. Mindegyiken a megengedett legnagyobb teljesítmény 1 watt lehet. A három ellenállást minden lehetséges módon összekapcsoljuk úgy, hogy mindig mindegyiken folyhasson áram.
\(\displaystyle a)\) Milyen határok között változhat a legnagyobb megengedett összteljesítmény?
\(\displaystyle b)\) Melyik kapcsolás esetén lehet a legnagyobb összteljesítmény pontosan 2 watt?
Közli: Varga Zsuzsa, Szeged
(4 pont)
P. 5288. Egy akvárium fala \(\displaystyle d=12\) mm vastagságú, \(\displaystyle n_\text{ü}= {3}/{2}\) törésmutatójú üvegből készült. Az akváriumban \(\displaystyle n_\text{v}= 4/3\) törésmutatójú vízben úszkál egy halacska. Kívülről, az akvárium falára merőleges irányból nézve a fal külső felületétől mekkora távolságra lévőnek tűnik a halacskának az a pontja, amely valójában pontosan \(\displaystyle t=20\) cm távolságra van a fal külső felületétől?
Közli: Cserti József, Budapest
(4 pont)
P. 5289. Egy transzmissziós, nagy felbontású optikai rácsra, melynek rései függőlegesen állnak, párhuzamos, monokromatikus fénynyalábot bocsátunk. Kísérletünkben a fénynyaláb merőleges az optikai rácsra, és a rácson való áthaladás után első rendben \(\displaystyle 30^\circ\)-kal térül el jobbra is és balra is. Ezután a rácsot a középső rés mint tengely körül \(\displaystyle 30^\circ\)-kal elforgatjuk. Milyen irányokban lép ki most fénynyaláb a rácsból?
Közli: Radnai Gyula, Budapest
(5 pont)
P. 5290. Homogén elektromos mező \(\displaystyle P\) pontjából egy pontszerű, negatív töltésű részecskét lövünk ki az elektromos térre merőleges \(\displaystyle \boldsymbol v_0\) kezdősebességgel. Az \(\displaystyle \boldsymbol E\) elektromos térerősségre és a \(\displaystyle \boldsymbol v_0\) sebességvektorra merőleges, homogén mágneses mező is jelen van. A kétféle mezőt egy, az elektromos térerősségre merőleges sík választja el egymástól az ábra szerint. Mekkora a mágneses indukcióvektor nagysága, ha a részecske visszatér a \(\displaystyle P\) pontba?
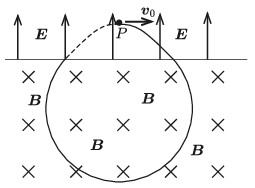
(Az egész elrendezés vákuumban van, és a nehézségi erő hatása a részecskére elhanyagolható.)
Közli: Németh László, Fonyód
(5 pont)
P. 5291. Egy szénmonoxid-érzékelő berendezés akkor ad riasztó jelzést, ha a CO-gáz sűrűsége a levegőben eléri a \(\displaystyle 4\cdot10^{-6} \mathrm{kg/m}^3\) értéket.
\(\displaystyle a)\) Hány CO-molekulát lélegzik be ilyenkor az ember egyetlen \(\displaystyle 500 \mathrm{cm}^3\)-es lélegzetvétellel?
\(\displaystyle b)\) Mekkora egy CO-molekula átlagos energiája a tüdőben \(\displaystyle 37\;{}^\circ\)C-on?
\(\displaystyle c)\) Mekkora a sebessége egy átlagos energiával rendelkező CO-molekulának?
Egyetemi felvételi feladat nyomán
(4 pont)
P. 5292. A \(\displaystyle \beta^-\)-bomló \(\displaystyle {}^{14}\mathrm{C}\) felezési ideje 5568 év. Egy bizonyos mennyiségű szénben a 14-es izotóp kezdeti aktivitása 12 MBq volt.
\(\displaystyle a)\) Hány atommag bomlott el az első percben?
\(\displaystyle b)\) Hány mag bomlott el az első 10 ezer évben?
\(\displaystyle c)\) Mekkora volt a kezdeti szén 14-es izotóp össztömege?
\(\displaystyle d)\) A kezdethez képest mennyi idő múlva lesz a szénben a 14-es izotóp tömege \(\displaystyle 1 \mu \mathrm{g}\)?
Közli: Zsigri Ferenc, Budapest
(4 pont)
P. 5293. Egy feketedoboz tetején sok kivezetés van. Tudjuk, hogy belül minden kivezetéspár közé egy-egy ismeretlen ellenállást forrasztottak. Hogyan mérhetjük meg két tetszőleges pont közé kötött ellenállás értékét, ha csupán ellenállásmérőnk és tetszőleges számú röpzsinórunk van?
Közli: Vladár Károly, Kiskunhalas
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

