A KöMaL 2021. márciusi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2021. április 15-én LEJÁRT. |
I. 532. Az angol ABC 26 betűjének kölcsönösen egyértelműen megfeleltetjük az 1-től 26-ig terjedő egészeket. Ismerjük \(\displaystyle N\) darab szó (\(\displaystyle 1< N\le 200\)) egyes betűinek megfelelő számok összegét mindegyik szóra, de magát az eredeti betű-szám megfeleltetést nem.
Készítsünk programot, amely meghatározza a különböző szavak és azok értéke alapján a lehető legtöbb betű számértékét az alább leírt műveletsor segítségével.
Standard bemenet: az első sor a szavak \(\displaystyle N\) számát tartalmazza, az ezt követő \(\displaystyle N\) sor soronként egy szót és annak értékét tartalmazza szóközzel elválasztva. A szavak legalább 3, de legföljebb 10 betűsök.
Standard kimenet: írjuk ki ABC-sorrendben azon betűket és értéküket, amelyek meghatározhatók az alább leírt módszerrel. Ha egyik betű értéke sem meghatározható, akkor írjuk ki az ,,Egyetlen betű-szám megfeleltetést sem találtam'' mondatot.

A megoldáshoz vezető eljárás addig ismétli az alábbi két lépést, amíg talál új betű-szám megfeleltetést:
\(\displaystyle a)\) keres olyan szót, amelyben pontosan egy ismeretlen értékű betű van, és megállapítja annak értékét;
\(\displaystyle b)\) összehasonlítja a szavakat, és ha talál két olyan szót, amely egy ismeretlen értékű betűben tér el egymástól, akkor ismét meghatározza az ismeretlen betű számértékét.
A fenti példában a satu és tas szavak alapján meghatározza az u betű értékét, ami így 14 lesz. Ezután az apu és apa szavak összehasonlításából megkapja az a betű értékét, ami 3. Ezt követően az apa szóból a p betűt kapjuk, ami 16, majd a kapu szóból a k értékét, ami 24. További betű-szám megfeleltetést nem találunk, így kiírjuk ABC sorrendben az eddigi találatokat.
Beküldendő egy i532.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.
(10 pont)
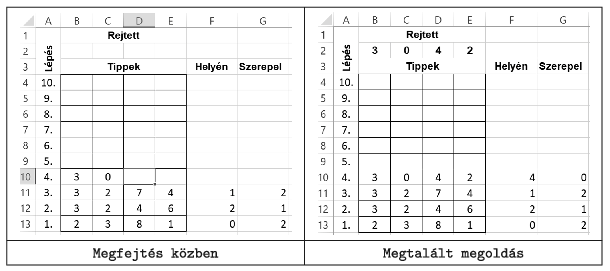
I. 533. Készítsük el a Mastermind játék számjegyes változatát táblázatkezelővel. A szabályok a következők:
– A játékot ketten játsszák, a feladó és a kitaláló. A kitaláló játékosnak maximum 10 lépése van, hogy a feladó négy számjegyből álló rejtett sorozatát kitalálja.
– A számjegyek nem ismétlődhetnek sem a rejtett, sem a tippsorozatban.
– Miután a feladó begépelte a szabályoknak megfelelő számnégyest, azok eltűnnek és kezdődhet a kitaláló tippelése. Ha a feladó nem a szabályok szerinti számnégyest szeretne feladni, akkor az ne váljon rejtetté.
– Minden tippelés sorában a jelzések azt mutatják, hogy hány számjegy van jó helyen, és hány szerepel a rejtett számban, de a tippben nem jó helyen. Az eltalált és jó helyen levő számjegyek száma az első; az eltalált, de rossz helyen levő számjegyek száma a második jelzés.
A táblázatot készítsük fel arra, hogy a helyesen, számjegyek ismétlődése nélkül beírt ,,Rejtett'' számok ne jelenjenek meg, amíg a tippek segítségével eltalált és jó helyen levő számjegyek száma négy nem lesz. A jelzések se jelenjenek meg addig, amíg a kitaláló a szabályoknak nem megfelelően adja meg a tippet, illetve nincs mind a négy cella kitöltve. A tippek számára a mintának megfelelően 10 sort készítsünk elő.
Segédszámításokat a H oszloptól jobbra végezhetünk, melyek értelmezését feliratokkal segítsük. Megoldási módszerünket mutassuk meg, tehát ezeket a cellákat ne rejtsük el.
Beküldendő egy tömörített i533.zip állományban a munkafüzet, valamint egy rövid leírás, amelyben szerepel az alkalmazott táblázatkezelő neve és verziószáma.
(10 pont)
I. 534. A Nemzetközi Sakkszövetség (Fédération Internationale des Échecs, FIDE) honlapján elérhető a világ jelenleg és korábban versenyszerűen sakkozó játékosainak eredményességét mutató Élő-pontszám és a versenyzők néhány más adata. Töltsük le a 2021. februári ranglistát, melynek elérhetősége a következő: http://ratings.fide.com/download/standard_feb21frl.zip. Tömörítsük ki az állományt, majd mentsük a benne lévő szöveges állományt sakk.txt néven. Töröljük az állomány első sorát, így a megmaradt szöveg 363\(\displaystyle \,\)272 sakkozó adatait tárolja azonos formátumban.
A fájl táblázatos kinézetét szóközök segítségével alakították ki. Minden sor pontosan 135 karaktert tartalmaz (csak az angol ABC karakterei, valamint számok és írásjelek fordulnak benne elő). A 16–76. karakterhelyen található balra igazítva a versenyző neve, a 77–79. karakterhelyen a versenyző országának hárombetűs rövidítése (a magyaroknál a szokásos HUN), a 81. karakterhelyen a versenyző nemét jelző betű (angol rövidítéssel M vagy F), a 114–117. karakterhelyen a versenyző aktuális Élő-pontszáma, és a 127–130. karakterhelyen a versenyző születési éve. A többi adatra nem lesz szükségünk a feladatok megoldása során.
Készítsünk programot sakk néven, amely megoldja a következő feladatokat. A feladatok megoldása során mindig írjuk ki a feladat sorszámát. Törekedjünk a mintának megfelelő kommunikációra a felhasználóval. Az ékezetek nélküli kiírás is megfelelő.
1. Olvassuk végig a szöveges állományt, és tároljuk el a fájl azon sorainak adatait, amelyek magyar versenyzőkről szólnak, tehát a magyar versenyzők nevét, nemét, Élő-pontszámát és születési évét. A név ne tartalmazza a fájlban a név után írt szóközöket, az Élő-pontszám és a születési év legyen egész érték.
2. Adjuk meg, hogy hány női, és hány férfi sakkozónk szerepel a listában.
3. Adjuk meg a legmagasabb Élő-pontszámmal rendelkező férfi és női sakkozónk nevét, pontszámát és születési évét.
4. Állapítsuk meg és írjuk ki, hogy hány olyan női versenyzőink van, aki 1990-ben vagy az után született, és Élő-pontszáma legalább 2000.
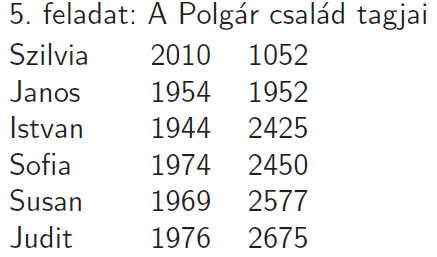
5. A Polgár családból többen is szerepelnek a listán. Adjuk meg a családtagok keresztnevét, születési dátumát és Élő-pontszámát táblázatos elrendezésben. A lista legyen a családtagok Élő-pontszáma szerint növekvő sorrendben.
6. Polgár Judit minden idők legkiválóbb női sakkozója, 1989-től 2005-ig vezette a női ranglistát, legmagasabb Élő-pontszáma 2735 volt. Adjuk meg, hogy kik azok a sakkozóink, akik legalább akkora pontszámmal rendelkeznek, mint Polgár Judit jelenleg. A listában a nevek a magyar írásmód szerint szerepeljenek. Tegyünk zárójelek között egy csillagot (*) azoknak a versenyzőknek a neve után, akiknek pontszáma eléri Polgár Judit egykor legmagasabb, 2735-ös pontszámát. A lista elemeit vesszővel és szóközzel válasszuk el egymástól, és zárjuk őket ponttal.
Minta program kimenet:
1. feladat: az adatok beolvasása
2. feladat:
A listában 5855 férfi és 603 női sakkozónk szerepel 3. feladat:
A legmagasabb pontszámú férfi versenyzőnk Rapport, Richard
Pontszáma: 2763
Születési éve: 1996
A legmagasabb pontszámú női versenyzőnk Polgar, Judit
Pontszáma: 2675
Születési éve: 1976
4. feladat:
33 olyan női sakkozónk van, aki 1990-ben vagy az után született, és Élő-pontszáma legalább 2000
6. feladat: Akik elérték Polgár Judit mai pontszámát:
Almasi Zoltan, Rapport Richard(*).
Beküldendő egy i534.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.
(10 pont)
 |
I/S-jelű feladatokA beküldési határidő 2021. április 15-én LEJÁRT. |
I/S. 52. Bergengóciában \(\displaystyle N\) darab város van, melyek 1-től \(\displaystyle N\)-ig számozottak. Jelenleg semelyik kettő sincs összekötve autópályával, így a király útépítési projektet hirdet. Pontosan akkor szeretné az \(\displaystyle x\) és \(\displaystyle y\) sorszámú városokat összekötni autópályával (\(\displaystyle x< y\)), ha az \(\displaystyle x\) szám osztója az \(\displaystyle y\)-nak, de nincs olyan \(\displaystyle z\) sorszám, amely osztható \(\displaystyle x\)-szel és osztója \(\displaystyle y\)-nak. Azaz, ha a szabály alapján \(\displaystyle x\) összeköthető \(\displaystyle z\)-vel és \(\displaystyle z\) összeköthető \(\displaystyle y\)-nal, akkor \(\displaystyle x\) és \(\displaystyle y\) között nem lehet út. (A várost saját magával nem kötjük össze.)
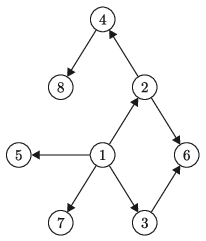
A király tanácsadójaként adjuk meg, hogy \(\displaystyle N\) város esetén hány autópályát kell építtetnie a királynak a leírt szabályok alapján.
Bemenet: az első és egyetlen sor a városok \(\displaystyle N\) számát tartalmazza.
Kimenet: a kimenet első és egyetlen sorába írjuk az építtetendő utak számát.
| Példa bemenet | Példa kimenet |
| 8 | 8 |
Korlátok: \(\displaystyle 1\le N\le 1\,000\,000\). Időkorlát: 0,4 mp.
Értékelés: A pontok 30%-a kapható, ha \(\displaystyle N< 100\). A pontok 60%-a kapható, ha \(\displaystyle N< 10\,000\).
Beküldendő egy is52.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2021. április 15-én LEJÁRT. |
S. 151. Egy versenyen \(\displaystyle N\) diák vett részt, minden versenyzőnek \(\displaystyle N\) feladatot kellett megoldana. A diákok minden feladatra egy 1 és \(\displaystyle K\) közötti egész számot kaptak értékelésként. A versenybizottság egy \(\displaystyle N\) sorból és \(\displaystyle N\) oszlopból álló táblázatban összegyűjtötte az összes diák összes feladatának értékelését. Az \(\displaystyle i\)-edik sor az \(\displaystyle i\)-edik diák megoldásaira kapott pontokat tartalmazza, a \(\displaystyle j\)-edik oszlop a \(\displaystyle j\)-edik feladatra beküldött megoldások értékelését tartalmazza. Ha egy diák egy feladatra nem küldött be megoldást, akkor ott a 0 szám szerepel.
A versenybizottság észrevette, hogy minden feladathoz találhatunk legalább egy olyan diákot, aki nem oldotta meg a feladatot, és minden diákhoz találhatunk legalább egy olyan feladatot, amelyet az adott diák nem oldott meg. Vagyis a táblázat minden oszlopában és minden sorában szerepel legalább egy 0 érték.
Adjuk meg, hogy hány különböző értékelő táblázat lehet (két táblázat különböző, ha van legalább egy elemük, amelyben különböznek). A táblázatok száma nagyon nagy is lehet, ezért a szám \(\displaystyle 10^{9}+7\)-tel vett osztási maradékát adjuk meg.
Bemenet: az első sor tartalmazza a szóközzel elválasztott \(\displaystyle N\) és \(\displaystyle K\) számokat.
Kimenet: adjuk meg a lehetséges táblázatok számát modulo \(\displaystyle 10^{9}+7\).
| Példa bemenet | Példa kimenet |
| 2 1 | 7 |
Lehetséges táblázatok \(\displaystyle N=2\) és \(\displaystyle K=1\) esetén:

Korlátok: \(\displaystyle 2\le N \le {10}^{5}\), \(\displaystyle 2\le K\le {10}^{9}\). Időkorlát: 0,4 mp.
Értékelés: a pontok 40%-a kapható, ha \(\displaystyle N \le 100\). További 40% kapható, ha \(\displaystyle N \le 5000\).
Beküldendő egy s151.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

