A KöMaL 2021. márciusi matematika feladatai

K-jelű feladatok A beküldési határidő 2021. április 12-én LEJÁRT.

---

K. 689. Egy kosárlabdázó a szezon 6., 7., 8. és 9. mérkőzésén rendre 23, 14, 11 és 20 pontot szerzett. A pontátlaga a 9. mérkőzés után nagyobb volt, mint az 5. mérkőzés után. Az átlaga a 10. mérkőzés után 18 fölé ment. Mennyi az a legkisebb pontszám, amelyet a 10. mérkőzésen megszerezve elérhette ezt az állapotot?

(6 pont)

megoldás, statisztika

---

K. 690. Peti gondolt egy pozitív egész számra és huszonhárom állítást fogalmazott meg a számmal kapcsolatban, melyek közül kettő szomszédos nem igaz, de a többi igaz.
1. Osztható 2-vel.
2. Osztható 3-mal.
3. Osztható 4-gyel.
\(\displaystyle \vdots\)
23. Osztható 24-gyel.

Peti a lehető legkisebb ilyen számra gondolt. Melyik ez a szám?

(6 pont)

megoldás, statisztika

---

K. 691. Az \(\displaystyle ABCDEFGH\) szabályos nyolcszög 2 egység hosszú \(\displaystyle BC\) és \(\displaystyle GF\) oldalára befelé a \(\displaystyle BCIM\) és az \(\displaystyle FGKL\) négyzetet rajzoljuk. Mekkora a területe annak a téglalapnak, amelyet az \(\displaystyle AH\), \(\displaystyle KL\), \(\displaystyle ED\) és \(\displaystyle IM\) egyenesek határolnak?

(6 pont)

megoldás, statisztika

---

K. 692. Legfeljebb hány egymással nem egybevágó rácstéglalapra lehet felbontani egy \(\displaystyle 6\times6\)-os négyzetet? Adjunk példát a felbontásra.

(6 pont)

megoldás, statisztika

---

K. 693. Az \(\displaystyle ABCD\) érintőnégyszög beírt körének középpontja \(\displaystyle O\). Mutassuk meg, hogy a \(\displaystyle DOC\sphericalangle\) és a \(\displaystyle BOA\sphericalangle\) összege \(\displaystyle 180^{\circ}\).

(6 pont)

megoldás, statisztika

C-jelű feladatok A beküldési határidő 2021. április 12-én LEJÁRT.

---

C. 1658. Egy körlapot felosztunk hat egybevágó körcikkre. Mindegyikbe beleírunk egy kört, mely érinti a körcikk határoló ívét és két sugarát. A hat kör együttes területe az eredeti kör területének hányadrészét fedi le?

(5 pont)

megoldás, statisztika

---

C. 1659. Az \(\displaystyle AB\) szakasz \(\displaystyle A\) pontjából induló \(\displaystyle a\) félegyenes a szakasszal \(\displaystyle 0^\circ< \alpha<90^{\circ}\)-os, a \(\displaystyle B\)-ből induló \(\displaystyle b\) félegyenes pedig \(\displaystyle 0^\circ<\beta<90^{\circ}\)-os szöget zár be. A két félegyenes az \(\displaystyle AB\) egyenese által meghatározott két különböző félsíkban helyezkedik el. Az \(\displaystyle AB\) átmérőjű kör az \(\displaystyle a\)-t \(\displaystyle A_1\)-ben, a \(\displaystyle b\)-t pedig \(\displaystyle B_1\)-ben metszi másodszor. Az \(\displaystyle A_1B_1\) átmérőjű kör az \(\displaystyle a\)-ra illeszkedő egyenest \(\displaystyle A_2\)-ben, a \(\displaystyle b\)-re illeszkedő egyenest pedig \(\displaystyle B_2\)-ben metszi másodszor. Milyen összefüggés van \(\displaystyle \alpha\) és \(\displaystyle \beta\) között, ha \(\displaystyle A_1B_1\) és \(\displaystyle A_2B_2\) merőlegesek?

(5 pont)

megoldás, statisztika

---

C. 1660. Egy \(\displaystyle 61\times61\)-es sakktábla négyzeteire elhelyezzük a pozitív egész számokat a bal felső sarokból indulva és a tábla sorainak megfelelően haladva \(\displaystyle 1\)-től \(\displaystyle 61^2\)-ig. Ezután első lépésben minden beírt szám előjelét negatívra változtatjuk. Második lépésben minden páros szám előjelét megváltoztatjuk, harmadik lépésben minden \(\displaystyle 3\)-mal osztható szám előjelét, és így tovább, amíg a lépés lehetséges. Mindezt elvégezve a táblán hány olyan \(\displaystyle 1\times2\)-es téglalap lesz, amelyben a számok összege negatív?

(5 pont)

megoldás, statisztika

---

C. 1661. Lottó Ottó, aki retteg a csökkenéstől, hagyományos lottót játszik. Itt 90 számból húznak ki öt számot. Ottó csak a következő feltételeknek eleget tevő számötöst jelöli be: az öt szám számjegyeit tekintve egy számjegy csak maximum egyszer szerepelhet, illetve miután leírta egymás mellé az öt számot növekvő sorrendben, a számjegyeknek is növekednie kell. Pl. 1, 2, 3, 46, 78. Hány, a feltételeknek megfelelő számötös létezik?

Javasolta: Berkó Erzsébet (Szolnok)

(5 pont)

megoldás, statisztika

---

C. 1662. Az \(\displaystyle a>0\) valós paraméter mely értéke esetén lesz az \(\displaystyle x^2+a=\sqrt{x-a}\) egyenletnek pontosan egy megoldása a valós számok halmazán? Mi ekkor az egyenlet megoldása?

(5 pont)

megoldás, statisztika

---

C. 1663. A \(\displaystyle k_1\) és \(\displaystyle k_2\) körök az \(\displaystyle E\) pontban kívülről érintik egymást. Az \(\displaystyle f\) és \(\displaystyle g\) egyenesek áthaladnak az \(\displaystyle E\) ponton. A két kör egyik közös külső érintője a \(\displaystyle k_1\), \(\displaystyle k_2\) köröket rendre a \(\displaystyle C\), \(\displaystyle D\) pontokban érinti. Bocsássunk merőlegeseket a \(\displaystyle C\) pontból az \(\displaystyle f\), \(\displaystyle g\) egyenesekre és kössük össze a merőlegesek talppontjait, így kapjuk a \(\displaystyle h\) egyenest. Hasonlóképpen adódik a \(\displaystyle D\) pontból kiindulva az \(\displaystyle m\) egyenes. Bizonyítsuk be, hogy \(\displaystyle h\) és \(\displaystyle m\) merőleges egymásra.

(5 pont)

megoldás, statisztika

---

C. 1664. Az \(\displaystyle ABCDEF\) konvex hatszög \(\displaystyle AD\), \(\displaystyle BE\), \(\displaystyle CF\) átlóinak mindegyike felezi a hatszög területét. Bizonyítsuk be, hogy ezek az átlók egy pontban metszik egymást.

(5 pont)

megoldás, statisztika

B-jelű feladatok A beküldési határidő 2021. április 12-én LEJÁRT.

---

B. 5158. Az \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) és \(\displaystyle D\) pontokra a síkon \(\displaystyle AB<CB\) és \(\displaystyle CD<AD\) teljesül. Mutassuk meg, hogy az \(\displaystyle AB\) és \(\displaystyle CD\) szakaszok nem metszik egymást.

(3 pont)

megoldás, statisztika

---

B. 5159. Oldjuk meg a pozitív egész számok halmazán a

\(\displaystyle \left[\frac{2020-x}{x-1}\right]+\left[\frac{2021+x}{x+1}\right]=82 \)

egyenletet, ahol \(\displaystyle [c]\) a \(\displaystyle c\) szám egészrészét jelöli.

Javasolta: Tatár Zsuzsanna Mária (Esztergom)

(4 pont)

megoldás, statisztika

---

B. 5160. Mennyi lehet \(\displaystyle x+y+z\) értéke, ha

\(\displaystyle \sqrt{x-1}+2\sqrt{y-4}+3\sqrt{z-9}=\frac{x+y+z}{2}? \)

Javasolta: Szalai Máté (Szeged)

(3 pont)

megoldás, statisztika

---

B. 5161. A \(\displaystyle 100\times 100\)-as sakktáblára letettünk \(\displaystyle 800\) L-tetrominót. Mutassuk meg, hogy letehetünk még egy L-tetrominót a táblára. A tetrominók nem fednek át, és mindegyik pontosan a sakktábla \(\displaystyle 4\) mezőjét fedi. L-tetrominó alatt az ábrán látható alakzatot, elforgatottjait és tükrözöttjeit értjük.

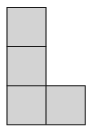
(6 pont)

megoldás, statisztika

---

B. 5162. Az \(\displaystyle ABC\) háromszög oldalai 9, 10 és 17 egység hosszúak. Mekkora az \(\displaystyle ABC\) háromszög külső szögfelezői által meghatározott háromszög területe?

Javasolta: Tatár Zsuzsanna Mária (Esztergom)

(5 pont)

megoldás, statisztika

---

B. 5163. Az \(\displaystyle ABC\) derékszögű háromszög \(\displaystyle C\) csúcsából induló, a legrövidebb oldalhoz közelebbi szögharmadoló az \(\displaystyle AB\) átfogót \(\displaystyle T\)-ben, a háromszög körülírt körét \(\displaystyle D\)-ben metszi. Mekkorák a háromszög hegyesszögei, ha a \(\displaystyle D\)-ből a befogók egyeneseire bocsátott merőlegesek talppontjai és \(\displaystyle T\) egy egyenesen vannak?

(4 pont)

megoldás, statisztika

---

B. 5164. Két játékos 3 győzelemig tartó kő-papír-olló párbajt játszik. Tegyük fel, hogy mindketten minden menetben véletlenszerűen (egymástól és a korábbi mutatásoktól függetlenül), \(\displaystyle \frac13 : \frac13 : \frac13\) eséllyel választják ki, hogy mit mutatnak. Adjuk meg a menetek számának várható értékét.

(5 pont)

megoldás, statisztika

---

B. 5165. Legyen \(\displaystyle k\) egy adott pozitív egész. Van-e olyan \(\displaystyle f \colon \mathbb{N} \to \mathbb{N}\) függvény, amelyre

\(\displaystyle f(x) + f\big(f(x)\big) = x + k \)

minden \(\displaystyle x \in \mathbb{N}\) esetén?

Javasolta: Lovas Márton (Budapest)

(6 pont)

megoldás, statisztika

A-jelű feladatok A beküldési határidő 2021. április 12-én LEJÁRT.

---

A. 795. A következő játékot játsszák \(\displaystyle n\) emberrel: adott \(\displaystyle n+1\) kalap, melyek meg vannak számozva \(\displaystyle 1\)-től \(\displaystyle n+1\)-ig. Az emberek szemét bekötik, és mindegyikük fejére feltesznek egyet az \(\displaystyle n+1\) kalap közül (a megmaradó kalapot elrejtik). Ezután az embereket sorba állítják, és leveszik a szemükről a kötést (mindegyik ember az előtte állókon lévő kalapok számait látja). Ezután hátulról előrefelé haladva mindegyik játékos sorban megtippeli a fején lévő kalap számát, de a tippek között nem lehet két egyforma (a játékosok hallják egymás tippjét).

Legfeljebb hány biztos találata lehet az \(\displaystyle n\) embernek, ha a játék ismertetése után megegyezhetnek egy közös taktikában?

Javasolta: Kiss Viktor (Budapest)

(7 pont)

statisztika

---

A. 796. Legyen \(\displaystyle ABCD\) egy húrnégyszög, melynek \(\displaystyle AB\) és \(\displaystyle CD\) oldalegyenesei a \(\displaystyle P\), \(\displaystyle BC\) és \(\displaystyle DA\) oldalegyenesei pedig a \(\displaystyle Q\) pontban metszik egymást. A \(\displaystyle P\) pontból az \(\displaystyle BC\) és \(\displaystyle DA\) oldalegyenesekre állított merőlegesek talppontjai \(\displaystyle K\) és \(\displaystyle L\), a \(\displaystyle Q\) pontból a \(\displaystyle AB\) és \(\displaystyle CD\) oldalegyenesekre állított merőlegesek talppontjai \(\displaystyle M\) és \(\displaystyle N\). Az \(\displaystyle AC\) átló felezőpontja legyen \(\displaystyle F\).

Bizonyítandó, hogy az \(\displaystyle FKN\) és \(\displaystyle FLM\) háromszögek körülírt körei és a \(\displaystyle PQ\) egyenes egy ponton megy át.

Balogh Ádám Péter (Szeged) ötlete alapján

(7 pont)

statisztika