A KöMaL 2021. áprilisi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2021. május 17-én LEJÁRT. |
M. 404. Az ábra szerint felfüggesztett vékony falú labdát kis kitéréssel lendítsük ki a fonalak síkjára merőlegesen, majd mérjük meg a lengésidőt (\(\displaystyle T_1\)). Ezután a nyugalomban lévő labdát forgassuk el kissé a függőleges tengelye körül, és mérjük meg a torziós lengésidőt (\(\displaystyle T_2\)). A mért értékekből számítsuk ki a \(\displaystyle \frac{T_1}{T_2}\) arányt!
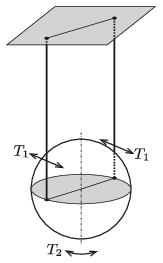
Közli: Németh László, Fonyód
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2021. május 17-én LEJÁRT. |
G. 741. Tegyük fel, hogy a hóbortos ötleteiről ismert multimilliárdos, Elon Musk úgy akarja közvetlenül meghatározni a Föld körül geostacionárius pályán keringő műholdak számát, hogy ugyanennek a pályának a közvetlen közelébe juttat egy számláló műholdat, amely nem nyugatról keletre, hanem éppen ellenkezőleg, keletről nyugatra halad. Mennyi idő alatt számolja meg ez a műhold az összes, a Földhöz viszonyítva álló műholdat?
(3 pont)
G. 742. Egy egyenes lejtő és egy 20 kg tömegű láda közötti súrlódás olyan nagy, hogy a láda magától nem csúszik lefelé. Ezt a ládát a lejtő aljától a tetejéig 3,0 kJ munkával tudjuk felhúzni, míg a ládát a lejtő tetejéről az aljáig 1,0 kJ munkával lehet eljuttatni. (A húzóerő mindkét esetben párhuzamos a lejtő síkjával, a mozgatás pedig lassú.) Mekkora a lejtő magassága?
(3 pont)
G. 743. Egy megpakolt konyhabútor egyik felső szekrénye egy olyan \(\displaystyle m = 40\) kg tömegű téglatest, melynek ,,mélysége'' \(\displaystyle a = 40\) cm, magassága \(\displaystyle b = 75\) cm, tömegközéppontja pedig a geometriai középponttal esik egybe. A szekrényt a fallal érintkező két felső csúcsánál egy-egy tiplis csavarral rögzítik (az ábrán ezek egymást fedve a \(\displaystyle P\) pontban találhatók). A szekrény a fallal csak az alsó éle mentén érintkezik. Legalább mekkora húzóerőt kell kibírnia a rögzítéseknek külön-külön, hogy a csavarok ne szakadjanak ki a falból? (A falnál a súrlódást hanyagoljuk el!)
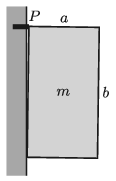
(4 pont)
G. 744. Az ábrán látható áramkör négy egyforma, \(\displaystyle 10~\Omega\)-os ellenállásból és egy telepből áll.
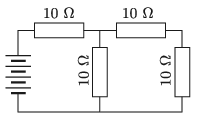
\(\displaystyle a)\) Mekkora a telep kapocsfeszültsége, ha a legtöbb Joule-hőt termelő ellenállás elektromos teljesítménye 360 W?
\(\displaystyle b)\) Mekkora a többi ellenállás teljesítménye?
(4 pont)
 |
P-jelű feladatokA beküldési határidő 2021. május 17-én LEJÁRT. |
P. 5315. Egy kerékpáros 9 km/h egyenletes sebességgel halad vízszintes terepen, majd 20 másodperc alatt egyenletesen felgyorsul 18 km/h sebességre. Mekkora lesz a kerék egy külső pontjának gyorsulása közvetlenül a gyorsítás befejezése után? A kerék átmérője 72 cm. Mekkora utat tett meg és hányat fordult a kerék a gyorsítás ideje alatt?
Közli: Kobzos Ferenc, Dunaújváros
(3 pont)
P. 5316. Vízszintes, érdes asztallapon nyugvó \(\displaystyle m_1\) tömegű korongnak centrális, egyenes ütközéssel nekicsúszik egy \(\displaystyle v_0= 5\) m/s sebességgel érkező, \(\displaystyle m_2 = 1\) kg tömegű másik korong. A csúszási súrlódás együtthatója az egyes korongokra nézve \(\displaystyle \mu_1 = 0{,}1\) és \(\displaystyle \mu_2 = 0{,}25\).
\(\displaystyle a)\) Mekkora a kezdetben nyugvó korong tömege, ha az abszolút rugalmas ütközés után egyszerre állnak meg?
\(\displaystyle b)\) Milyen távol lesznek ekkor egymástól?
\(\displaystyle c)\) Az ütközéstől számítva mennyi idő múlva állnak meg?
Közli: Holics László, Budapest
(5 pont)
P. 5317. Egy iskolai bemutató távcső tengelye telihold idején pontosan a Hold közepe felé irányul. Az iskolaudvaron mozdítatlanul álló távcsőben a Hold képe éppen kitölti a látómezőt. Mennyi idő telik el a telihold feltűnése és eltűnése között?
Közli: Radnai Gyula, Budapest
(3 pont)
P. 5318. Egyes elképzelések szerint a sötét anyag hipotetikus részecskéi (blacktonok) úgy mozognak az intergalaktikus térben, hogy a sebességükkel ellentétes irányú erő hat rájuk. Az erő nagyságának sebességfüggését ma még nem ismerjük, csak annyit tudunk, hogy két különböző sűrűségű térrészben a fékezőerők aránya minden sebességnél ugyanakkora. Bizonyos \(\displaystyle v_0\) kezdősebességű blackton-részecskék egy ritkább térrészben 3 fényévnyi út megtétele után állnak meg, a sűrűbb térben pedig 2 fényévnyi úton fékeződnek le. Mekkora út megtétele után állnak meg a \(\displaystyle v_0\) kezdősebességű blacktonok, ha egy 1,5 fényév vastagságú, sűrűbb réteg után a ritkább anyageloszlású térbe jutnak?
Közli: Gnädig Péter, Vácduka
(5 pont)
P. 5319. Vízszintes síkon elcsúsztatunk egy \(\displaystyle m\) tömegű, \(\displaystyle \ell\) hosszúságú, vékony, homogén pálcát. Egy pillanatban a pálca egyik végének sebességvektora \(\displaystyle \boldsymbol v_1\), a másiké \(\displaystyle \boldsymbol v_2\). Mekkora ebben a pillanatban
\(\displaystyle a)\) a pálca lendülete;
\(\displaystyle b)\) a tömegközéppontra vonatkozó perdülete;
\(\displaystyle c)\) a teljes mozgási energiája?
Közli: Gelencsér Jenő, Kaposvár
(5 pont)
P. 5320. Függőleges falból két azonos magasságban bevert szög áll ki, melyek távolsága \(\displaystyle L\). A szögekre egy kötelet fektetünk úgy, hogy annak belógása \(\displaystyle H\). Becsüljük meg a kötél teljes hosszát, ha tudjuk, hogy
\(\displaystyle a)\) \(\displaystyle H\ll L\);
\(\displaystyle b)\) \(\displaystyle L \ll H\).
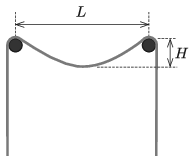
A súrlódás mindenütt elhanyagolható.
Közli: Berke Martin, Budapest
(5 pont)
P. 5321. Függőleges, alul zárt hengerekben lévő, különböző tömegű, súrlódásmentesen mozgó dugattyúk azonos térfogatú, azonos hőmérsékletű hélium-, illetve oxigéngázt zárnak el. A gázokat lassan azonos hőmérsékletre melegítjük fel. A melegítés során az oxigén belsőenergia 2,5-szer, a tágulási munkája pedig 220 J-lal nagyobb, mint a hélium esetében.
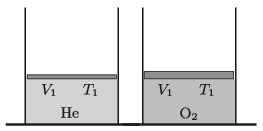
\(\displaystyle a)\) Határozzuk meg a gázok kezdeti nyomásának arányát!
\(\displaystyle b)\) Mennyit hőt közöltünk a melegítés során a héliummal, illetve az oxigénnel?
Közli: Kotek László, Pécs
(4 pont)
P. 5322. Egy digitális fényképezőgép téglalap alakú szenzorának mérete: \(\displaystyle 23{,}5~\mathrm{mm} \times 15{,}6~\mathrm{mm}\), és ez a szenzor \(\displaystyle 6045\times 4003\) képpontot képes rögzíteni. Oldalról, 20 méter távolságból lefényképezünk a géppel egy 40 km/h sebességgel haladó motorcsónakot.
Mekkorának válasszuk a 35 mm gyújtótávolságú objektívvel felszerelt fényképezőgép expozíciós idejét, ha nem szeretnénk, hogy a motorcsónak képe ,,bemozduljon'' (életlenné váljon)?
Közli: Széchenyi Gábor, Budapest
(4 pont)
P. 5323. Az ábrán látható ellenállásrendszer \(\displaystyle A\) pontjában \(\displaystyle I = 40\) mA erősségű elektromos áram be-, a \(\displaystyle B\) csúcsnál kifolyik.
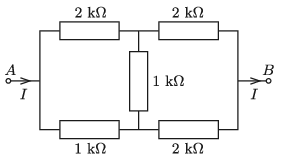
\(\displaystyle a)\) Mekkora elektromos áram folyik az egyes ellenállásokon?
\(\displaystyle b)\) Mekkora az elektromos teljesítmény az egyes ellenállásokon?
\(\displaystyle c)\) Mekkora egyetlen ellenállással lehetne helyettesíteni ezt az ellenállásrendszert?
Közli: Simon Péter, Pécs
(4 pont)
P. 5324. Közép-Afrikában, egy Kinshasa melletti uránbányában az egyik műszak által kibányászott kőzet uránszurokérc (\(\displaystyle \mathrm{U}_3\mathrm{O}_8\)) tartalma 10 tonna volt.
Becsüljük meg, hogy mennyi rádium volt a kőzetben!
Közli: Zsigri Ferenc, Budapest
(5 pont)
P. 5325. Egy kamrában hosszú ideje működik egy fagyasztóláda. A hőmérséklet a ládán belül \(\displaystyle -20\;{}^\circ\mathrm{C}\), a kamrában \(\displaystyle 25\;{}^\circ\mathrm{C}\), a kamrán kívül, a lakás többi részén pedig \(\displaystyle 20\;{}^\circ\mathrm{C}\) van. Mekkora lesz hosszú idő után a kamrában a hőmérséklet, ha még egy ugyanilyen fagyasztóládát bekapcsolunk?
Feltehetjük, hogy a lakás hőmérséklete a kamrán kívül nem változik. A hűtőládákat tekintsük ideális Carnot-gépeknek, amelyek termosztátja úgy van beállítva, hogy belül fenntartja a \(\displaystyle -20\;{}^\circ\mathrm{C}\)-os hőmérsékletet.
Közli: Vigh Máté, Biatorbágy
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

