A KöMaL 2023. januári matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2023. február 10-én LEJÁRT. |
K. 749. Aladdin egy szelencében 5 pénzérmét talált, melyekből az egyik hamis. Azt, hogy melyik az, csak Abu, a kismajom tudja. Aladdin 3 érmét kiválaszthat, ebből egyet Abunak ad, cserébe Abu megmondja a másik kettőről, van-e közte hamis. Abu valódi érméért igazat mond, és hazudik, ha hamis érmét kap. Lehet-e legfeljebb három kérdéssel azonosítani a hamis érmét?
Róka Sándor (Nyíregyháza) javaslata alapján
(5 pont)
K. 750. Peti mindig ugyanakkora sebességgel megy az iskolába, de néha siet, ilyenkor kétszer akkora sebessséggel halad. Tegnap az iskolába menet az út harmadáig sétált, aztán pedig sietett, ma pedig 6 perccel többet sétált, mint sietett. Hány perccel hosszabb a mai útja a tegnapinál?
(5 pont)
K. 751. Van öt csokigolyónk, melyek külsőre ugyanúgy néznek ki. Három csokigolyó mindegyikének tömege 20 g, egy csokigolyó 19 g tömegű, egy pedig 21 g-os. Rendelkezésünkre áll egy kétkarú mérleg. Igazoljuk, hogy a 19 g tömegű csokigolyót három méréssel kiválaszthatjuk, de kevesebbel nem.
(5 pont)
 |
K/C-jelű feladatokA beküldési határidő 2023. február 10-én LEJÁRT. |
K/C. 752. A 10, 11, 12, 13, 14, 15, 16, 17 számok közül \(\displaystyle k\)-féleképpen választhatunk ki legalább két olyan számot, amelyek összege osztható 3-mal. Fejezzük ki \(\displaystyle k\) segítségével, hogy hányféleképpen választhatunk ki a 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 számok közül legalább kettőt úgy, hogy az összegük osztható legyen 3-mal. (Két kiválasztás akkor különböző, ha nem ugyanazok a számok szerepelnek benne.)
(5 pont)
K/C. 753. Az \(\displaystyle A\) csúcsú szög egyik szárán lévő \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\) és \(\displaystyle E\) pontokra, illetve a másik szárán lévő \(\displaystyle F\), \(\displaystyle G\), \(\displaystyle H\) és \(\displaystyle I\) pontokra igaz, hogy \(\displaystyle AB=BG=GD=DI=IE=EH=HC=CF=FA\). Mutassuk meg, hogy a \(\displaystyle CEH\) és az \(\displaystyle IGD\) háromszögek szabályosak.
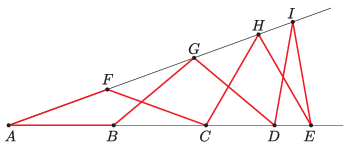
(5 pont)
 |
C-jelű feladatokA beküldési határidő 2023. február 10-én LEJÁRT. |
C. 1748. Mutassuk meg, hogy egy egységsugarú körbe írt húrnégyszög legrövidebb oldalának hossza nem lehet nagyobb \(\displaystyle \sqrt{2}\)-nél.
(Kanadai feladat)
(5 pont)
C. 1749. Számítsuk ki \(\displaystyle \sqrt[\scriptsize 3]{K}\) pontos értékét, ha \(\displaystyle K\) a \(\displaystyle 2025\) összes pozitív osztójának a szorzata.
Javasolta: Kozma Katalin Abigél (Győr)
(5 pont)
C. 1750. Az \(\displaystyle O_1\) középpontú \(\displaystyle k_1\) és az \(\displaystyle O_2\) középpontú \(\displaystyle k_2\) körök közös pontjai \(\displaystyle M\) és \(\displaystyle N\). Az \(\displaystyle M\) ponton áthaladó szelő a \(\displaystyle k_1\) kört az \(\displaystyle A\), a \(\displaystyle k_2\) kört a \(\displaystyle B\) pontban metszi úgy, hogy \(\displaystyle A\) a \(\displaystyle k_2\) körre, \(\displaystyle B\) a \(\displaystyle k_1\) körre nézve külső pont. Az \(\displaystyle AO_1\) és \(\displaystyle BO_2\) egyenesek közös pontja \(\displaystyle P\). Az \(\displaystyle N\) és a \(\displaystyle P\) pont az \(\displaystyle O_1O_2\) egyenes által meghatározott két félsík közül ugyanabba esik. Mutassuk meg, hogy \(\displaystyle P\) illeszkedik az \(\displaystyle O_1NO_2\) háromszög körülírt körére.
Javasolta: Bíró Bálint (Eger)
(5 pont)
C. 1751. Legyenek \(\displaystyle a\) és \(\displaystyle b\) olyan pozitív valós számok, melyekre \(\displaystyle a^2+b^2=\frac{2}{9}\). Igazoljuk, hogy
\(\displaystyle \frac{1}{2-3a}+\frac{1}{2-3b} \ge 2. \)
Javasolta: Szmerka Gergely (Budapest)
(5 pont)
C. 1752. Hatan sorban állnak. Sokat kell várniuk, ezért játékból egy bizonyos szabály szerint sorrendet cserélnek és azt háromszor egymás után végrehajtják. Egy ilyen szabály (ún. permutáció) például: az 1. a 3. helyre áll, a 2. az 1. helyre, a 3. a 2. helyre, a 4. a 6. helyre, az 5. az 5. helyen marad, végül a 6. a 4. helyre áll. Mekkora a valószínűsége, hogy legalább az egyikük az eredeti helyére kerül?
Javasolta: Kozma Katalin Abigél (Győr)
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2023. február 10-én LEJÁRT. |
B. 5286. Melyik az a legkisebb pozitív egész \(\displaystyle n\), amelyre az \(\displaystyle \underbrace{11\ldots1}_{n}\) szám osztható a \(\displaystyle \underbrace{33\ldots3}_{100}\) számmal (\(\displaystyle 10\)-es számrendszerben)?
(Brazil feladat)
(3 pont)
B. 5287. Két kör kívülről érinti egymást. A körök középpontján átmenő egyenes a köröket – az érintési ponton kívül – az \(\displaystyle A\) és a \(\displaystyle B\) pontokban metszi. A körök egyik közös külső érintőjének az érintési pontjai \(\displaystyle P\) és \(\displaystyle Q\). Igazoljuk, hogy az \(\displaystyle AP\) és \(\displaystyle BQ\) egyenesek a körök közös belső érintőjén metszik egymást. (Az \(\displaystyle A\) és \(\displaystyle P\) pontok vannak az egyik körön, a \(\displaystyle B\) és \(\displaystyle Q\) pontok pedig a másikon.)
Javasolta: Molnár István Ádám (Miskolc)
(3 pont)
B. 5288. Két játékos a következő játékot játssza egy \(\displaystyle 8 \times 8\)-as sakktáblán. A játékosok felváltva lépnek, egy lépésben egy játékos a két szomszédos mezőt elválasztó szakaszok egyikét sárgára színezi. Az a játékos veszít, akinek a lépése után először jön létre egy olyan sokszög, amelynek minden oldala sárga. Melyik játékosnak van nyerő stratégiája?
(Amerikai versenyfeladat alapján)
(4 pont)
B. 5289. Legyenek \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) és \(\displaystyle d\) olyan nemnegatív valós számok, amelyekre \(\displaystyle a+b+c+d=1\). Bizonyítsuk be, hogy
\(\displaystyle \frac{1}{a^2+1}+\frac{1}{b^2+1}+\frac{1}{c^2+1}+\frac{1}{d^2+1} \ge \frac72. \)
Javasolta: Szoldatics József (Budapest)
(5 pont)
B. 5290. Oldjuk meg az alábbi egyenletet a pozitív egész számok halmazán:
\(\displaystyle 3^n+4^n+\ldots+{(n+2)}^n= {(n+3)}^n. \)
Javasolta: Káspári Tamás (Paks)
(6 pont)
B. 5291. Az \(\displaystyle ABC\) háromszög beírt körének középpontja \(\displaystyle I\), körülírt körének középpontja \(\displaystyle O\). Mekkora a háromszög területe, ha \(\displaystyle OIA\sphericalangle=90^\circ\), \(\displaystyle AI=89\) és \(\displaystyle {BC=160}\)?
Javasolta: Róka Sándor (Nyíregyháza)
(5 pont)
B. 5292. Adott egy \(\displaystyle k\) kör és a belsejében a \(\displaystyle P\) és a \(\displaystyle Q\) pontok. Szerkesszünk (írjuk le a szerkesztés menetét – az elemi szerkesztési lépéseket, mint pl. szög felezése, tengelyes tükrözés, nem kell részletezni – és indokoljuk az eljárás helyességét; magát a szerkesztést nem kell papíron elvégezni) a \(\displaystyle P\) és \(\displaystyle Q\) pontokon át olyan kört, amely a \(\displaystyle k\) kört két átellenes pontjában metszi. A \(\displaystyle P\) és \(\displaystyle Q\) pontok helyzetétől függően hány megoldása van a feladatnak?
Javasolta: Kató Gábor (Kápolnásnyék)
(5 pont)
B. 5293. Legyen \(\displaystyle p\) egy prímszám. Legfeljebb hány egész együtthatós polinom adható meg úgy, hogy semelyik kettő különbsége ne legyen minden egész helyen \(\displaystyle p^2\)-tel osztható?
Javasolta: Pach Péter Pál (Budapest)
(6 pont)
 |
A-jelű feladatokA beküldési határidő 2023. február 10-én LEJÁRT. |
A. 842. Egy faluban \(\displaystyle n\) ember él, akik klubokba járnak (egy ember több klubnak is lehet tagja). Akárhogy választunk ki néhány (de legalább egy) klubot, lehet találni a faluban egy olyan embert, aki a kiválasztott klubok közül páratlan soknak tagja. Mutassuk meg, hogy a klubok száma legfeljebb \(\displaystyle n\).
Javasolta: Pálvölgyi Dömötör (Budapest)
(7 pont)
A. 843. Legyen \(\displaystyle N\) azon \(\displaystyle n\) pozitív egészek halmaza, melyekre tetszőleges \(\displaystyle k\) pozitív egész esetén teljesül, hogy ha \(\displaystyle n\mid k^k-1\), akkor \(\displaystyle n\mid k-1\). Bizonyítsuk be, hogy ha \(\displaystyle n_1, n_2\in N\), akkor a legnagyobb közös osztójuk is \(\displaystyle N\)-ben van.
(7 pont)
A. 844. Az \(\displaystyle ABC\) háromszög beírt köre a \(\displaystyle BC\), \(\displaystyle AC\) és \(\displaystyle AB\) oldalakat rendre a \(\displaystyle D\), \(\displaystyle E\) és \(\displaystyle F\) pontban érinti. Legyen \(\displaystyle E'\) az \(\displaystyle E\) tükörképe a \(\displaystyle DF\) egyenesre, \(\displaystyle F'\) pedig \(\displaystyle F\) tükörképe a \(\displaystyle DE\) egyenesre. Messe az \(\displaystyle EF\) egyenes az \(\displaystyle AE'F'\) háromszög köréírt körét \(\displaystyle X\)-ben és \(\displaystyle Y\)-ban. Bizonyítsuk be, hogy \(\displaystyle DX=DY\).
Javasolta: Lovas Márton (Budapest)
(7 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

