KöMaL Problems in Mathematics, March 2006
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on April 10, 2006. |
K. 79. Rob the robot is shut up in a room. He starts moving in one direction and goes on in a straight line until he hits a wall. (A room does not have walls in its interior.) Then he turns to the right and continues in that direction. If he cannot turn right or he would collide in the wall, then he turns left instead and goes on in that direction. If he cannot turn either right or left then he switches himself off. Figure 1 shows a room in which if Rob starts from position 1, he will go around the room, end up at 1 again, and shut down there. Figure 2 shows a room in which if Rob starts from either 1 or 2, he will return to the starting point and shut down there. In Figure 3, if Rob starts from 1, he will end up at 2, and vice versa, and shut down there. (The grid in the figures is only for making it easier to follow Rob's path.) Draw a room in which there are 4 starting points: If Rob starts at 1, he will end up at 2 and shut down, starting at 2 he will end up at 3 and shut down, starting from 3 he will end up at 1 and shut down, and starting from 4 he will also end up at 4 and shut down.
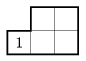
Figure 1
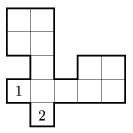
Figure 2
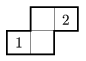
Figure 3
(6 pont)
solution (in Hungarian), statistics
K. 80. Polyminoes are like dominoes: they are made up of small squares that are joined together along whole sides. Define the ``boundary number'' of a polymino P as the number of different ways to place congruent copies of P around its boundary. (There must be a polymino touching it along each of its edges, and touching edges touch along their full length.) For example the boundary number of the cross is 2, since it can be bounded by its copies in the following two ways: (Arrangements that are mirror images of each other are considered different.) What is the boundary number of a 3×3 square (i.e. one consisting of 9 small squares)?
(6 pont)
solution (in Hungarian), statistics
K. 81. How many six-digit numbers of the form ABAABA are there can be expressed as a product of exactly four primes?
(6 pont)
solution (in Hungarian), statistics
K. 82. We have two cubes of not necessarily the same size with integer edges. They are placed on top of each other, so that the upper cube has a whole face touching a face of the lower cube. The volume of the solid obtained in this way expressed incube units is the same as the measure of the surface area in square units. How long are the edges of the original cubes?
(6 pont)
solution (in Hungarian), statistics
K. 83. Consider a convex hexagon in the plane with four distinct points given in its interior, such that no three points out of the vertices of the hexagon and the four given points lare collinear. The hexagon is dissected into triangles, such that the vertices are those of the hexagon and the given points. (All the 10 points must be used.) Show that the number of triangles obtained is always 12.
(6 pont)
solution (in Hungarian), statistics
K. 84. Is there a square number, such that the sum of its digits is 2006?
(6 pont)
 |
Problems with sign 'C'Deadline expired on April 18, 2006. |
C. 845. In an algebra class on the first of April, the students were practising. The task was to simplify the fraction
Agnes, who was the best at mathematics in the class, suggested that if the denominator is not zero, they should just cross out the threes in all the indices, that is, write
Check the result.
(5 pont)
solution (in Hungarian), statistics
C. 846. In how many different orders may the digits 0, 1, 2, 3, 4, 5, 6 form a seven-digit number divisible by four? (A number cannot start with 0.)
(5 pont)
solution (in Hungarian), statistics
C. 847. Find a line that halves both the area and the perimeter of the ``Egyptian'' triangle (the sides of which are 3, 4, 5).
(5 pont)
solution (in Hungarian), statistics
C. 848. Find the largest and smallest values of the expression
(5 pont)
solution (in Hungarian), statistics
C. 849. Evaluate cot x, given that cot x=sin x?
(5 pont)
 |
Problems with sign 'B'Deadline expired on April 18, 2006. |
B. 3892. The president of the Pyramid Bank lives in a fancy residential district outside the city. On weekdays, he is driven to the city in a car that leaves the bank in the city at the same time every morning, picks up the president and they arrive at the bank exactly when it opens. One morning, the driver called the president to say that something was wrong with the car and he would be late. So the president left home one hour earlier than usual on foot. Meanwhile, the driver fixed the car and still managed to leave the city at the usual time. He met the bank president on the way, picked him up, and they arrived at the bank 20 minutes before opening. How long did the president walk? (Assume that the speed of the car is constant, and picking up a passenger does not take any time.)
(3 pont)
solution (in Hungarian), statistics
B. 3893. Solve the equation
(x2+y2)3=(x3-y3)2
on the set of real numbers.
(3 pont)
solution (in Hungarian), statistics
B. 3894. The lines of the legs AB and CD of a trapezium ABCD intersect at the point M. A line e passing through M intersects the line AD at a point E different from A and D, and it intersects the line BC at F. The intersection of the diagonals is constructed in each of the trapezia ABFE and CDEF, denote them by P and Q. Show that PQ is parallel to the bases of the trapezia.
(3 pont)
solution (in Hungarian), statistics
B. 3895. The edges of a square based right prism are a=b=8, c=27 units long. Cut the prism into four parts, such that it is possible to put them together to form a cube.
(5 pont)
solution (in Hungarian), statistics
B. 3896. Consider the points where the lines of the altitudes of an acute scalene triangle intersect the perpendicular bisectors of the sides. Prove that these points determine two congruent triangles that are similar to the original triangle.
(4 pont)
solution (in Hungarian), statistics
B. 3897. For which values of n is it possible to assign values to the variables from the set {+1,-1} to make the equality
true?
(4 pont)
solution (in Hungarian), statistics
B. 3898. It is known that the line segments connecting the midpoints of the opposite edges of a tetrahedron are concurrent. Is it possible to select a point on each edge that divides the edge 1:2, such that the line segments connecting the selected points of opposite edges are concurrent?
(3 pont)
solution (in Hungarian), statistics
B. 3899. Is it possible for the product of four consecutive positive integers to be a perfect cube?
(5 pont)
solution (in Hungarian), statistics
B. 3900. Find all pairs (a1,a2) of positive integers, such that the sequence defined by the recurrence
is periodic.
(5 pont)
solution (in Hungarian), statistics
B. 3901. What is the locus of those points in the plane where the tangents drawn to a given parabola enclose a 30o angle?
(5 pont)
 |
Problems with sign 'A'Deadline expired on April 18, 2006. |
A. 395. Let 1<a<2 be a real number. (a) Show that there exists a unique sequence x1,x2,... of positive integers satisfying xi+1 xi2 for all indices i and
xi2 for all indices i and
(b) Prove that inequality xi+1>xi2 holds for infinitely many indices if and only if a is irrational.
(5 pont)
A. 396. The elements of families and
are finite sets, each having at most n elements. Suppose that for an arbitrary finite set F there exist
and
such that X
 Y
Y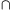 F=Ø. Prove that there exist
F=Ø. Prove that there exist and
such that X
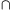 Y=Ø.
Y=Ø.
(5 pont)
A. 397. Given n unit circle (n 3) in the plane, their centers are O1,O2,...,On. Any line of the plane intersects at most two of them. Show that
3) in the plane, their centers are O1,O2,...,On. Any line of the plane intersects at most two of them. Show that
(5 pont)
Upload your solutions above.
