KöMaL Problems in Mathematics, January 2008
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on February 11, 2008. |
K. 151. In a survey carried out with a group of students, it turned out that 2/3 of the boys and 3/4 of the girls like raspberries. It also turned out that the same number of boys and girls liked raspberries. What fraction of the students taking part in the survey like raspberries?
(6 pont)
solution (in Hungarian), statistics
K. 152. 3% of the 800 inhabitants of the planet Awr have two heads. Half the remaining inhabitants have three heads, and the other half have only one. A shipment of fruits is arriving from the neighbouring planet Bwr: one delicious cwr for each head. How many, exactly?
(6 pont)
solution (in Hungarian), statistics
K. 153. Steve has a four-digit number in mind that Alex has to guess. Alex chooses a four-digit number, and Steve tells him how many digits it contains that stand in the appropriate position. [For example, if the number to find out is 1234 and the guess is 6231, then 2 digits are correct: 2 and 3. (The 1 does not count, since that is not in the right position.)] Alex had nine guesses: 2186, 5127, 6924, 4351, 5916, 8253, 4521, 6384, 8517. In each of the nine numbers, he guessed exactly one digit right, that is, each of the nine numbers contains exactly one digit that stands in the right position. What is the number that Steve has in mind?
(6 pont)
solution (in Hungarian), statistics
K. 154. The ratio of the difference, sum and product of two numbers is 1:7:24. What are the two numbers?
(6 pont)
solution (in Hungarian), statistics
K. 155. In the triangle shown in the Figure,  DAB=
DAB= ABC=60o, and
ABC=60o, and  CAB=
CAB= CBD. Prove that AD+CB=AB.
CBD. Prove that AD+CB=AB.
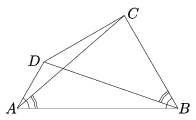
(6 pont)
solution (in Hungarian), statistics
K. 156. The lower part of the house (see the Figure) in the circle is a square, and the top is an equilateral triangle. Prove that the length of the side of the house equals the radius of the circle.
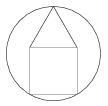
(6 pont)
 |
Problems with sign 'C'Deadline expired on February 15, 2008. |
C. 925. Show that the expression
has a constant value for all x and y for which it is meaningful and x+y=1.
(5 pont)
C. 926. A lecture hall has 24 lamps. Each lamp may operate 4 light bulbs at most. When the maintenance staff has installed four bulbs in some of the lamps, it became clear that the number of bulbs available was not enough. Then they continued with three bulbs per lamp, then two bulbs per lamp, and finished the job with one bulb per lamp. How many bulbs were missing if there were twice as many lamps with one bulb as with four bulbs, and there remained no bulbs at all for half as many lamps as those with three bulbs?
(5 pont)
solution (in Hungarian), statistics
C. 927. The length of the hypotenuse of a right-angled triangle is c, and its area is . Find the exact measures of the angles of the triangle.
(5 pont)
solution (in Hungarian), statistics
C. 928. The whole numbers are written down up to a certain number n divisible by 50, and then the multiples of 50 are cancelled. Prove that the sum of the remaining numbers is a perfect square.
(5 pont)
solution (in Hungarian), statistics
C. 929. The base edges and the lateral edges of a truncated pyramid of square base are all 4 units long. The sides of the top face are 2. What is the maximum possible distance between two vertices of the truncated pyramid?
(5 pont)
 |
Problems with sign 'B'Deadline expired on February 15, 2008. |
B. 4052. A path P1,P2,...,Pk in a simple graph is said to be a fan if the degree of every point Pi is i. What is the maximum number of points that a fan may have in a simple graph on n points?
Suggested by G. Mészáros
(4 pont)
solution (in Hungarian), statistics
B. 4053. The sequence of integers has infinitely many positive terms and infinitely many negative terms. For every n, the remainders of
divided by n are pairwise different. How many times does the number 2008 occur in the sequence?
(4 pont)
solution (in Hungarian), statistics
B. 4054. The radius of a circle inscribed in a triangle is r. The tangents drawn to the circle parallel to the sides cut three small triangles off the original triangle. Prove that the sum of the radii of the inscribed circles of the small triangles is also r.
(3 pont)
solution (in Hungarian), statistics
B. 4055. Prove that every number not greater than n! can be expressed as a sum of at most n different factors of the number n!.
(5 pont)
solution (in Hungarian), statistics
B. 4056. The orthocentre of an acute-angled triangle is M, the centre of its circumscribed circle is O, and its sides are a<b<c. The line of side c, the line of the altitude drawn to side b, and the line MO form a triangle that is similar to the original triangle but with opposite orientation. Find the angles of the triangle.
Suggested by J. Bodnár, Budapest
(4 pont)
solution (in Hungarian), statistics
B. 4057. Solve the equation x6-6x+5=0.
(4 pont)
solution (in Hungarian), statistics
B. 4058. The angles of a triangle are  ,
,  ,
,  . What is the largest possible value of sin
. What is the largest possible value of sin  sin
sin  cos
cos  +sin2
+sin2 ?
?
(4 pont)
solution (in Hungarian), statistics
B. 4059. O is a given point in the plane. Give an example for congruent triangles A and B, such that every circle centred at O has parts of the equal areas inside the triangles A and B.
Inspired by a problem of the Schweitzer Competition of 2007
(5 pont)
solution (in Hungarian), statistics
B. 4060. Determine all functions for which
f(x)+f(x+f(y))=2x+y
for all real values of x and y.
(4 pont)
solution (in Hungarian), statistics
B. 4061. Given the ABC and PQR triangles such that vertex A of triangle ABC bisects side QR. Vertex P bisects side BC. Line QR bisects angle BAC, and line BC bisects angle QPR. Prove that AB+AC=PQ+PR.
(5 pont)
 |
Problems with sign 'A'Deadline expired on February 15, 2008. |
A. 443. The perimeter of a certain convex hexagon is p. The midpoints of the sides form an inscribed hexagon such that all its angles are 120o and its perimeter is p1. Prove that
Vietnamese problem
(5 pont)
A. 444. Given a continuous function such that for any real number a>0, the sequence
converges to 0. Show that
.
Czech problem
(5 pont)
A. 445. Prove that for every prime number p and integer r there exists a nonnegative integer n for which .
(5 pont)
Upload your solutions above.
