KöMaL Problems in Mathematics, March 2012
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on April 10, 2012. |
K. 331. The task is to cross a desert with a car. The width of the desert is 600 km. The capacity of the petrol tank of the car is only enough for 400 km, and the car cannot carry fuel in any other way. The car can travel with an average speed of 50--60 km/h. It needs to start out at 8 a.m. and it is to arrive on the other side by 8 p.m. What is the minimum number of such cars needed, for one of them to be able to cross the desert, while the others return back? It is possible to transfer fuel from one car to another.
(6 pont)
solution (in Hungarian), statistics
K. 332. The sum of a few positive integers is 20. Their product is the number X. What is the maximum possible value of X?
(6 pont)
solution (in Hungarian), statistics
K. 333. The three interior angles of a triangle followed by the three exterior angles, in the appropriate order, form six consecutive terms of an arithmetic sequence. Find the measures of the angles of the triangle in degrees. (In an arithmetic sequence, the difference of the consecutive terms is constant, that is, the sequence increases uniformly.)
(6 pont)
solution (in Hungarian), statistics
K. 334. Alma measured and tabulated the distances (in steps) between fruit trees in the garden. How many steps is it from the walnut tree to the pear tree?
|
(6 pont)
solution (in Hungarian), statistics
K. 335. A peculiar calculator only has four buttons on it: 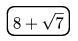 (eight plus root seven),
(eight plus root seven),  (addition),
(addition), 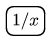 (reciprocal) and
(reciprocal) and  (equals) (see the figure).
(equals) (see the figure).
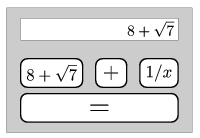
The calculator always carries out the operations with exact values, and it can also store the current value as a constant if the  button is pressed twice. That is, in subsequent calculations whenever the
button is pressed twice. That is, in subsequent calculations whenever the  button is pressed, the number is incremented by that value any number of times. (E.g. if the buttons
button is pressed, the number is incremented by that value any number of times. (E.g. if the buttons 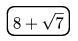



 are pressed, it will display
are pressed, it will display ). Prove that the result of the following sequence of operations is 1:
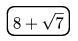
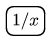


 ...
...  (56 times)
(56 times)

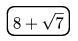

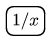


 ...
...  (15 times)
(15 times)
(6 pont)
solution (in Hungarian), statistics
K. 336. The concave 16-sided polygon in the figure is divided into four congruent squares and eight congruent rhombuses. The smaller angle of the rhombuses is 45 degrees. Given that the longer diagonal of the rhombuses is 10.7 cm, find the area of the 16-sided polygon.
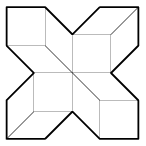
(6 pont)
 |
Problems with sign 'C'Deadline expired on April 10, 2012. |
C. 1115. Show that n2(n2-1)(n2-n-2) is divisible by 48 for all natural numbers n.
(5 pont)
solution (in Hungarian), statistics
C. 1116. Each side of a convex quadrilateral is divided into eight equal parts. Each dividing point is connected to the corresponding dividing point on the opposite side, as shown in the figure. The small quadrilaterals obtained in this way are coloured black and white in a chessboard pattern. Prove that the total area of the black quadrilaterals equals the total area of the white quadrilaterals.

(5 pont)
solution (in Hungarian), statistics
C. 1117. We have drawn a rectangle on squared paper, such that (its sides are lattice lines and) it consists of n small lattice squares. Prove that if the half of the number of lattice points on the boundary of the rectangle is added to the number of lattice points in its interior, and 1 is subtracted from the sum then the result will be n.
(5 pont)
solution (in Hungarian), statistics
C. 1118. Solve the equation on the set of real numbers.
(5 pont)
solution (in Hungarian), statistics
C. 1119. Two identical set squares(of 30, 60 and 90 degrees) are fixed together along their shorter legs of length 10 cm, as shown in the figure. Then an isosceles set square is placed on top. Is there enough room for a tennis ball of radius 3.2 cm in the interior of the tetrahedron obtained in this way?
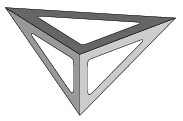
(5 pont)
 |
Problems with sign 'B'Deadline expired on April 10, 2012. |
B. 4432. There is a 98×98 chessboard on the monitor of a computer. With the mouse, you can select a rectangle bounded by lattice lines of the chessboard. If you click on the rectangle, each chessboard field inside it will change to the opposite colour. What is the minimum number of clicks needed to make the whole chessboard have the same colour.
(5 pont)
solution (in Hungarian), statistics
B. 4433. Solve the equation (1+x)8+(1+x2)4=82x4.
(3 pont)
solution (in Hungarian), statistics
B. 4434. Prove that every natural number not divisible by 10 can be multiplied by an appropriate natural number, such that the product is a palindromic number in decimal notation.
(4 pont)
solution (in Hungarian), statistics
B. 4435. T is the foot of the altitude drawn from vertex A of an acute-angled triangle ABC. The midpoint of side BC is F. The centres of the squares drawn over the sides AB and AC on the outside are K and L, respectively. Prove that KTFL is a cyclic quadrilateral.
(Suggested by Sz. Miklós, Herceghalom)
(4 pont)
solution (in Hungarian), statistics
B. 4436. Let x, y, z denote positive integers, such that . Prove that
.
(Suggested by J. Mészáros, Jóka)
(4 pont)
solution (in Hungarian), statistics
B. 4437. Given the centres of the circumscribed circle and two escribed circles of a triangle, construct the triangle.
(4 pont)
solution (in Hungarian), statistics
B. 4438. The angle bisectors of a triangle ABC intersect the opposite sides at the points A1, B1 and C1, respectively. For what triangles is it true that ?
(Matlap, Cluj-Napoca -- Kolozsvár)
(3 pont)
solution (in Hungarian), statistics
B. 4439. Given two different points B and C in the plane, determine the locus of those points A for which the altitude drawn from vertex A of the triangle ABC is the geometric mean of the line segments BC+AC and BC-AC.
(3 pont)
solution (in Hungarian), statistics
B. 4440. On a winter's day, an absent minded mathematician went on a walk with his old poodle along a long straight alley. He was so absorbed in his thoughts that when he finally thought of his dog, he had to realize that it was not near him. In the snowfall, he did not see further than 5 metres. He did not see the dog in front of him, he did not see it behind either, and he did not know which direction it had gone. After a little thinking, he went to look for his poodle. The old poodle can only walk half as fast as its master. The mathematician chose a searching strategy, such that the following condition should hold for the smallest possible value of the constant c: if the dog is at a distance x from him then he needs to cover a distance of at most cx to find it. What is this smallest value of c?
(5 pont)
solution (in Hungarian), statistics
B. 4441. The areas of the faces of a tetrahedron are a, b, c, d. The angle enclosed by the faces of areas a and b is  , the angle of b and c is
, the angle of b and c is  , and the angle of c and a is
, and the angle of c and a is  . Prove that d2=a2+b2+c2-2ab.cos
. Prove that d2=a2+b2+c2-2ab.cos  -2bc.cos
-2bc.cos  -2ca.cos
-2ca.cos  .
.
(5 pont)
 |
Problems with sign 'A'Deadline expired on April 10, 2012. |
A. 557. Show that the positive integers can be coloured with three colours in such a way that the equation x+y=z2 has no solution (x,y,z) consisting of distinct numbers with the same colour.
(Kolmogorov's Cup, 2011; a problem by F. Petrov and I. Bogdanov)
(5 pont)
A. 558. Prove that there exists a constant C>0 for which the following statement holds: if n is a positive integer and are sets such that every two of them has at least two, and every three of them has at most three elements in common, then N<Cn2.
(Proposed by: Z. Gyenes, Budapest)
(5 pont)
A. 559. The incircle of triangle ABC is k. The circle kA touches k and the segments AB and AC at at A', AB and AC respectively. The circles kB, kC and the points B', C' are defined analogously. The second intersection point of the circles A'B'AB and A'C'AC, other than A', is K. The line A'K meets k at R, other than A'. Prove that R lies on the radical axis of the circles kB and kC.
(Kolmogorov's Cup, 2011; a problem by F. Ivlev)
(5 pont)
Upload your solutions above.
