KöMaL Problems in Mathematics, September 2018
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on October 10, 2018. |
K. 589. A company regularly hires the same man to mow a certain grassy area. In addition to the labour cost, the man charges a call-out fee of 5000 forints (HUF, Hungarian currency). If he mows the grass three times a month, the labour cost is 1.8 times as much per occasion as it is in the case when he mows the grass four times a month, since in the former case the grass will grow higher which requires more work. On the whole, it is more economical for the company to have the grass mowed four times a month. What is the minimum possible labour cost per mowing in the case of 4 occasions a month, given that it is an integer multiple of 100 forints?
(6 pont)
solution (in Hungarian), statistics
K. 590. Andrew, Bill and Charlie participated in a running race. At the end, Bill and Carlie, respectively, were 15 metres and 35 metres behind when Andrew finished. When Bill finished, Charlie was still 22 metres behind him. What was the distance covered by the runners, given that each boy was running at a uniform speed?
(6 pont)
solution (in Hungarian), statistics
K. 591. A group of children participated in a bus excursion. In the luggage compartment of the bus, there is room for the luggage of one third of the children. The bus has 52 seats. The teachers are sitting on two seats. On each of the remaining seats, there is either a child sitting, or there is the luggage of a child. How many children are there on the trip if all seats are used?
(6 pont)
solution (in Hungarian), statistics
K. 592. Ann, Belle and Charlotte are doing a job together. The three of them finish it 6 hours sooner than Ann would finish it alone, 1 hour sooner than Belle would finish it alone, and they take half as much time together as Charlotte would take alone. If Ann and Belle work together without Charlotte, they finish the job in 80 minutes. How long would it take each girl Ann and Belle to do the job alone? (Express your answer in minutes.)
(6 pont)
solution (in Hungarian), statistics
K. 593. A disobedient class were trying to boycott the PE lesson. Therefore, when given the task of throwing a ball along the running track as far as they can, they threw the balls towards the fence instead, in the hope of getting the balls across the fence and halting the lesson while the balls are collected. 1/6 of the students threw 5 balls each, half the class threw 4 balls per student, one student threw 6 balls and all the rest of them threw 2 balls each. They managed to throw 75% of the balls over the fence. Since it took a lot of of time to get all these 66 balls back, the students were punished. They were made to run 3 laps each on the 200-metre running track. How many kilometres did they run altogether?
(6 pont)
 |
Problems with sign 'C'Deadline expired on October 10, 2018. |
C. 1490. What is the remainder if the number \(\displaystyle N=863\underbrace{99\ldots 9}_\text{2018 times}\) (with 2018 digits of 9 at the end) is divided by 32?
(5 pont)
solution (in Hungarian), statistics
C. 1491. The length of side \(\displaystyle AD\) of a rectangle \(\displaystyle ABCD\) is 1 cm. The angle bisector of \(\displaystyle \angle BAD\) and the perpendicular bisector of diagonal \(\displaystyle AC\) intersect on the side \(\displaystyle CD\). Find the exact length of side \(\displaystyle CD\).
(5 pont)
solution (in Hungarian), statistics
C. 1492. The solid in the figure consists of 15 unit cubes. In how many different ways is it possible to get from vertex \(\displaystyle A\) to vertex \(\displaystyle B\) along the grid lines if it is only allowed to move in the three directions indicated?
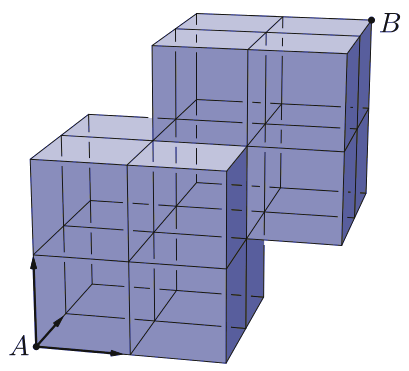
(5 pont)
solution (in Hungarian), statistics
C. 1493. A triangle of unit area has sides \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\), such that \(\displaystyle a\ge b\ge c\). Show that \(\displaystyle b\ge \sqrt2\,\).
(5 pont)
solution (in Hungarian), statistics
C. 1494. Prove that if \(\displaystyle p\) and \(\displaystyle q\) are twin primes greater than 3, then their arithmetic mean is divisible by 6 and the number greater by 1 than their product is divisible by 36.
(5 pont)
solution (in Hungarian), statistics
C. 1495. Consider the following sequence of equalities:
$$\begin{align*} 1 + 2 & = 3, \tag{1}\\ 4 + 5 + 6 & = 7 + 8, \tag{2}\\ 9 + 10 + 11 + 12 & = 13 + 14 + 15. \tag{3} \end{align*}$$By observing the rule, state the \(\displaystyle k\)th row, and prove your statement.
Proposed by Á. Kertész, Miami Beach
(5 pont)
solution (in Hungarian), statistics
C. 1496. Disks of radii 1, 2 and 3 cm are drawn about the vertices of a triangle. The three disks pairwise touch each other from outside. What is the area in the triangle that is not covered by the disks?
(5 pont)
 |
Problems with sign 'B'Deadline expired on October 10, 2018. |
B. 4966. Find the nineteenth positive integer in which the sum of the digits is 2018.
(3 pont)
solution (in Hungarian), statistics
B. 4967. Let \(\displaystyle P\) be an interior point of \(\displaystyle \triangle ABC\), and the midpoint of sides \(\displaystyle AB\), \(\displaystyle BC\) and \(\displaystyle CA\) are \(\displaystyle C_1\), \(\displaystyle A_1\) and \(\displaystyle B_1\), respectively. Through the points \(\displaystyle A_1\), \(\displaystyle B_1\) and \(\displaystyle C_1\), draw parallels to the lines \(\displaystyle AP\), \(\displaystyle BP\) and \(\displaystyle CP\), respectively. Show that these three lines are concurrent.
Proposed by J. Kozma, Szeged
(3 pont)
solution (in Hungarian), statistics
B. 4968. Solve the following simultaneous equations on the set of positive real numbers:
$$\begin{align*} \frac{1}{1+a + ab + abc} + \frac{1}{1+b + bc + bcd} + \frac{1}{1+c + cd + cda} + \frac{1}{1+d + da + dab} & = 1,\\ a+b+c+d & = 4. \end{align*}$$(4 pont)
solution (in Hungarian), statistics
B. 4969. The sides of a rectangle \(\displaystyle T\) are \(\displaystyle a\le b\). Given that the union of two appropriate disks of radius \(\displaystyle r\) covers \(\displaystyle T\) but this is impossible with two disks of radii smaller than \(\displaystyle r\), determine the length \(\displaystyle r\).
(4 pont)
solution (in Hungarian), statistics
B. 4970. A line \(\displaystyle e\) in the plane separates two given points \(\displaystyle A\) and \(\displaystyle B\) of the plane. On the line \(\displaystyle e\), select points \(\displaystyle P\) and \(\displaystyle Q\) such that \(\displaystyle \angle PAQ=90^{\circ}\). Show that there exists a point different from \(\displaystyle B\) that lies on all circles drawn through \(\displaystyle B\), \(\displaystyle P\) and \(\displaystyle Q\), independently of the choice of \(\displaystyle P\) and \(\displaystyle Q\).
Proposed by the class 11C of Fazekas Primary and Secondary School, Budapest
(5 pont)
solution (in Hungarian), statistics
B. 4971. For which primes \(\displaystyle p\) is there a positive integer \(\displaystyle a\) such that \(\displaystyle 1+a+a^2+\cdots+a^{p-1}\) is divisible by \(\displaystyle p^2\)?
(5 pont)
solution (in Hungarian), statistics
B. 4972. Let \(\displaystyle P\) be an interior point of an acute-angled triangle \(\displaystyle ABC\). Let \(\displaystyle D\), \(\displaystyle E\) and \(\displaystyle F\) be the orthogonal projections of \(\displaystyle P\) onto the sides, as shown in the figure. Outside the triangle, a square is drawn over each of the six line segments formed on the sides. The squares are then alternatively coloured by two colours according to the figure. Consider the two triangles formed by the lines of the ``outer'' sides of the squares with the same colour. Show that these two triangles are congruent.
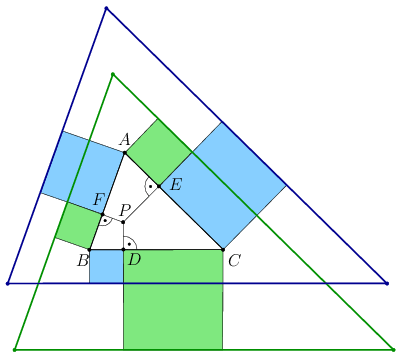
(6 pont)
solution (in Hungarian), statistics
B. 4973. Let \(\displaystyle a_1, a_2, \ldots, a_{2018}\) denote non-negative real numbers that add up to \(\displaystyle 1\). Find the largest possible value of the sum \(\displaystyle S = \sum_{i \ne j,\; i\mid j} a_ia_j\).
Based on an Argentinean problem
(6 pont)
 |
Problems with sign 'A'Deadline expired on October 10, 2018. |
A. 728. Floyd the flea makes jumps on the positive integers. On the first day he can jump to any positive integer. From then on, every day he jumps to another number that is not more than twice his previous day's place.
a) Show that Floyd can make infinitely many jumps in such a way that he never arrives at any number with the same sum of decimal digits as at a previous place.
b) Can the flea jump this way if we consider the sum of binary digits instead of decimal digits?
Dürer competition, 2015
(7 pont)
A. 729. In a cyclic quadrilateral \(\displaystyle ABCD\), the diagonals meet at point \(\displaystyle E\), the midpoint of side \(\displaystyle AB\) is \(\displaystyle F\), and the feet of perpendiculars from \(\displaystyle E\) to the lines \(\displaystyle DA\), \(\displaystyle AB\), and \(\displaystyle BC\) are \(\displaystyle P\), \(\displaystyle Q\), and \(\displaystyle R\), respectively. Prove that the points \(\displaystyle P\), \(\displaystyle Q\), \(\displaystyle R\), and \(\displaystyle F\) are concyclic.
Proposed by Máté Weisz, Szeged
(7 pont)
A. 730. Let \(\displaystyle F_n\) be the \(\displaystyle n\)th Fibonacci number (\(\displaystyle {F_1=F_2=1}\), \(\displaystyle {F_{n+1}=F_n+F_{n-1}}\)). Construct infinitely many positive integers \(\displaystyle n\) such that \(\displaystyle n\) divides \(\displaystyle F_{F_n}\) but \(\displaystyle n\) does not divide \(\displaystyle F_n\).
(7 pont)
Upload your solutions above.
