KöMaL Problems in Mathematics, February 2019

Problems with sign 'K' Deadline expired on March 11, 2019.

K. 614. In the increasing sequence of positive integers (starting with 1), find the 225th number that cannot be represented as a product of two consecutive integers.

(6 pont)

solution (in Hungarian), statistics

K. 615. Six points are selected in the interior of a square such that no three points among the 10 points (the vertices of the square and the six points) are collinear. From these 10 points, pairs of points are connected with line segments that do not intersect each other, and the process is continued until it is not possible to add a further line segment. What is the largest possible number of line segments that may be drawn in this way?

(6 pont)

solution (in Hungarian), statistics

K. 616. There are a lot of integers that can be represented as a sum of three perfect squares. For example, \(\displaystyle 1=1^2+0^2+0^2\), \(\displaystyle 14=3^2+2^2+1^2\), \(\displaystyle 20=4^2+2^2+0^2\). Show that 1991 cannot be represented as a sum of three perfect squares.

(6 pont)

solution (in Hungarian), statistics

K. 617. The diagonal \(\displaystyle AG\) of a rectangular block \(\displaystyle ABCDEFGH\) intersects the triangle \(\displaystyle BDE\) at point \(\displaystyle Q\). Prove that \(\displaystyle Q\) is the centroid of triangle \(\displaystyle BDE\).

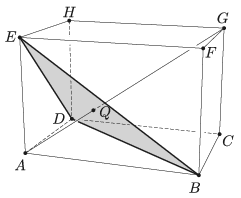
(6 pont)

solution (in Hungarian), statistics

K. 618. A positive integer \(\displaystyle n\) is said to be a ``strong'' number if its number of divisors is greater than the number of divisors of each positive integer less than \(\displaystyle n\). (For example, \(\displaystyle n=2\) is a strong number, because it has two divisors, while \(\displaystyle n=1\) has only one. But \(\displaystyle n=3\) is not a strong number, because it has two divisors similarly to a smaller integer \(\displaystyle n=2\).)

\(\displaystyle a)\) Find all strong numbers greater than 2 but less than 30.

\(\displaystyle b)\) Is \(\displaystyle 2^3\cdot3^4\cdot5\) a strong number?

(6 pont)

solution (in Hungarian), statistics

Problems with sign 'C' Deadline expired on March 11, 2019.

C. 1525. A team in a football championship had 33 points after 15 games they played. The 15 games included all three kinds of outcome: winning, losing, and draw. How many games did they win? (3 points are scored for winning a game, 0 for losing and 1 for each team in the case of a draw.)

(5 pont)

solution (in Hungarian), statistics

C. 1526. The circumscribed circle of a square is reflected in each side. Let \(\displaystyle T\) denote the area of the circle that touches these reflections in the interior of the square. Let \(\displaystyle t\) denote the area of the circle that touches one reflection and the circumscribed circle, both from the inside. Determine the smallest possible value of \(\displaystyle \frac{T}{t}\).

(5 pont)

solution (in Hungarian), statistics

C. 1527. If two appropriate numbers in the sequence \(\displaystyle 1, 2, \dots , n\) are erased, the sum of the remaining numbers will be 2019. Find all possible pairs of numbers that may be erased.

(5 pont)

solution (in Hungarian), statistics

C. 1528. What positive integer may \(\displaystyle n\) denote if the number obtained by erasing the last three digits of the number \(\displaystyle n^3\) is \(\displaystyle n\) itself?

Proposed by S. Róka, Nyíregyháza

(5 pont)

solution (in Hungarian), statistics

C. 1529. Prove that every right-angled triangle can be divided into \(\displaystyle 3k+2\) isosceles triangles where \(\displaystyle k\) is any positive integer.

(5 pont)

solution (in Hungarian), statistics

C. 1530. Is it possible to group all the integers from 1 to 51 into sets of three such that the sum of the numbers in each set should be a prime?

(5 pont)

solution (in Hungarian), statistics

C. 1531. The base of a right prism is a regular triangle, and its volume is \(\displaystyle 2~\textrm{dm}^3\). What is the minimum possible surface area of the prism?

(5 pont)

solution (in Hungarian), statistics

Problems with sign 'B' Deadline expired on March 11, 2019.

B. 5006. The bases of a trapezium \(\displaystyle ABCD\) are \(\displaystyle AB\) and \(\displaystyle CD\), the intersection of the diagonals is \(\displaystyle M\). Diagonal \(\displaystyle AC\) bisects the angle \(\displaystyle BAD\), \(\displaystyle AM=BC\) and \(\displaystyle BM=CD\). Find the angles of the trapezium.

Based on a problem of the National Competition

(4 pont)

solution (in Hungarian), statistics

B. 5007. We have \(\displaystyle 3n+1\) coins, \(\displaystyle n\) of which have 0 on one side and \(\displaystyle 11\) on the other. Another \(\displaystyle n\) coins have 0 on one side and \(\displaystyle 44\) on the other, and the remaining \(\displaystyle n+1\) coins have 0 on one side and \(\displaystyle 99\) on the other. All the coins are tossed at the same time. What is the probability that the sum of the resulting numbers is divisible by 7? (The coins are fair coins.)

(4 pont)

solution (in Hungarian), statistics

B. 5008. A circle \(\displaystyle k_A\) is centred at \(\displaystyle A\), and a circle \(\displaystyle k_B\) is centred at \(\displaystyle B\). Line \(\displaystyle l_1\) touches \(\displaystyle k_A\) at \(\displaystyle A_1\) and \(\displaystyle k_B\) at \(\displaystyle B_1\). Line \(\displaystyle l_2\) touches \(\displaystyle k_A\) at \(\displaystyle A_2\) and \(\displaystyle k_B\) at \(\displaystyle B_2\). Prove that the orthogonal projections of the line segments \(\displaystyle A_1A_2\) and \(\displaystyle B_1B_2\) onto the line \(\displaystyle AB\) are of equal length.

(3 pont)

solution (in Hungarian), statistics

B. 5009. Given that \(\displaystyle x^2+y^2+z^2=3\), where \(\displaystyle x\), \(\displaystyle y\), \(\displaystyle z\) are positive numbers, prove that \(\displaystyle 2^{\tfrac1x} + 2^{\tfrac1y} + 2^{\tfrac1z} \ge 6\).

Proposed by V. N. Nguyen, Vietnam

(3 pont)

solution (in Hungarian), statistics

B. 5010. The inscribed circle of an acute-angled triangle \(\displaystyle ABC\) touches the sides at the points \(\displaystyle A_0\), \(\displaystyle B_0\) and \(\displaystyle C_0\). The points of tangency of the excircles on the lines of the sides are \(\displaystyle A_1\), \(\displaystyle B_1\) and \(\displaystyle C_1\); \(\displaystyle A_2\), \(\displaystyle B_2\) and \(\displaystyle C_2\); \(\displaystyle A_3\), \(\displaystyle B_3\) and \(\displaystyle C_3\), respectively. Let \(\displaystyle T_i\) denote the area of triangle \(\displaystyle A_iB_iC_i\) (\(\displaystyle i=0,1,2,3\)). Show that

\(\displaystyle \frac{1}{T_0}=\frac{1}{T_1}+\frac{1}{T_2}+\frac{1}{T_3}. \)

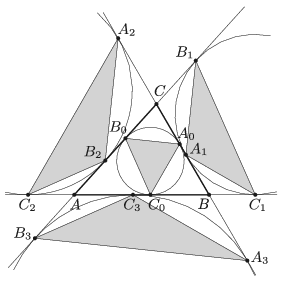
(5 pont)

solution (in Hungarian), statistics

B. 5011. We are given 6 points in the plane such that all pairwise distances are different. Show that there exist two triangles with the following property: each vertex is among the 6 given points, and the two triangles share a side in common such that this side is the shortest one in one triangle and the longest one in the other.

Proposed by S. Róka, Nyíregyháza

(5 pont)

solution (in Hungarian), statistics

B. 5012. Let \(\displaystyle f(x)\) be a polynomial with integer coefficients. Let \(\displaystyle f^{(n)}\) denote the \(\displaystyle n\)-fold application of \(\displaystyle f\):

\(\displaystyle f^{(n)}(x)=\underbrace{f\Big(f\big(\ldots f}_{n}(x)\ldots\big)\!\Big). \)

Let \(\displaystyle k(f)\) denote the smallest positive integer \(\displaystyle k\) for which \(\displaystyle f^{(k)}(x)\equiv x\pmod{13}\) holds for all integers \(\displaystyle x\), provided that there exists such a \(\displaystyle k\), and let \(\displaystyle k(f)=0\) otherwise. Prove that there is a maximum value of \(\displaystyle k(f)\), and determine this maximum value.

(6 pont)

solution (in Hungarian), statistics

B. 5013. The excircle of triangle \(\displaystyle ABC\) opposite to vertex \(\displaystyle A\) touches line \(\displaystyle AC\) at point \(\displaystyle B_1\). The line segment \(\displaystyle BB_1\) intersects the excircle at \(\displaystyle B_2\), and the tangent drawn to the excircle at \(\displaystyle B_2\) intersects side \(\displaystyle BC\) at \(\displaystyle B_3\). Similarly, the inscribed circle of the triangle touches side \(\displaystyle AB\) at point \(\displaystyle C_1\), line segment \(\displaystyle CC_1\) intersects the incircle at \(\displaystyle C_2\), and the tangent drawn to the incircle at \(\displaystyle C_2\) intersects side \(\displaystyle BC\) at \(\displaystyle C_3\). Prove that \(\displaystyle B_2B_3=C_2C_3\).

(6 pont)

solution (in Hungarian), statistics

Problems with sign 'A' Deadline expired on March 11, 2019.

A. 743. The incircle of tangential quadrilateral \(\displaystyle ABCD\) intersects diagonal \(\displaystyle BD\) at \(\displaystyle P\) and \(\displaystyle Q\) (\(\displaystyle BP<BQ\)). Let \(\displaystyle UV\) be the diameter of the incircle perpendicular to \(\displaystyle AC\) (\(\displaystyle BU<BV\)). Show that the lines \(\displaystyle AC\), \(\displaystyle PV\) and \(\displaystyle QU\) pass through one point.

Based on problem 2 of IOM 2018, Moscow

(7 pont)

statistics

A. 744. Show that for every odd integer \(\displaystyle N>5\) there exist vectors \(\displaystyle \mathbf{u},\mathbf{v},\mathbf{w}\) in (three-dimensional) space which are pairwise perpendicular, not parallel with any of the coordinate axes, have integer coordinates, and satisfy \(\displaystyle |\mathbf{u}|=|\mathbf{v}|=|\mathbf{w}|=N\).

Based on problem 2 of the 2018 Kürschák contest

(7 pont)

solution (in Hungarian), statistics

A. 745. We have attached a clock hand to every face of a convex polyhedron. Each hand always points towards a neighboring face (two faces of the polyhedron are neighbors if they share an edge). At the end of every minute, exactly one of the hands turns clockwise to point at the next face. Suppose that the hands on neighboring faces never point towards one another. Show that one of the hands makes only finitely many turns.

(7 pont)

solution (in Hungarian), statistics