KöMaL Problems in Mathematics, January 2020
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on February 10, 2020. |
K. 644. A box contained a total of 70 blue and green cubes. Four times as many blue cubes were removed as green cubes, so there remained 7 times as many green cubes as blue cubes in the box. How many cubes of each colour were there originally?
(6 pont)
solution (in Hungarian), statistics
K. 645. What will be the remainder if \(\displaystyle 1+4+7+\dots+2020\) is divided by 8?
(6 pont)
solution (in Hungarian), statistics
K. 646. We have three machines. Each of them has two input channels and one output channel. As represented in the diagram, the machines carry out some well defined sequence of operations with the numbers obtained through the input channels, and display the final result as output.
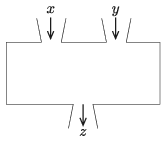
Machine A displays \(\displaystyle x\cdot y\), machine B displays \(\displaystyle x^2+y\), and machine C displays \(\displaystyle 5\cdot x+3\cdot y\) where \(\displaystyle x\) and \(\displaystyle y\) stand for the first and second input numbers, respectively. The machines A, B and C are connected by attaching the outputs of two machines to the inputs of the third one. What is the largest possible output that may be obtained from the third machine if the inputs of the first two machines are the same, \(\displaystyle x=4\) and \(\displaystyle y=7\)?
(6 pont)
solution (in Hungarian), statistics
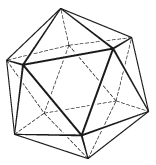
K. 647. An icosahedron made of paper is cut along some edges to unfold in the plane and obtain the net of the solid. How many edges need to be cut?
(6 pont)
solution (in Hungarian), statistics
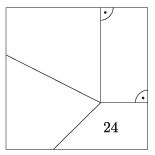
K. 648. The sides of a square are divided into three equal parts. An interior point of the square is connected to one of the dividing points on each side, as shown in the figure, to form four quadrilaterals. Given the area of one quadrilateral (see figure), determine the areas of the other quadrilaterals.
(6 pont)
 |
Problems with sign 'C'Deadline expired on February 10, 2020. |
C. 1581. Find all positive integers \(\displaystyle n\) for which \(\displaystyle n!\) ends in exactly \(\displaystyle 19\,531\) zeros.
(5 pont)
solution (in Hungarian), statistics
C. 1582. Let \(\displaystyle ABP\), \(\displaystyle BCQ\), \(\displaystyle CDR\), \(\displaystyle DAS\) denote the regular triangles drawn on the sides of paralellogram \(\displaystyle ABCD\) on the outside. What requirements does the parallelogram need to meet in order for \(\displaystyle PQRS\) to be a square?
(5 pont)
solution (in Hungarian), statistics
C. 1583. In the Cartesian coordinate plane, represent the points for which the following inequality holds:
\(\displaystyle |x|+|y|+|x+y|\le 2. \)
What is the area of the resulting figure?
(Croatian problem)
(5 pont)
solution (in Hungarian), statistics
C. 1584. What is the maximum area of a square that can be obtained from a triangular sheet of paper with sides 3 cm, 4 cm and 5 cm by cutting along at most three straight lines?
(5 pont)
solution (in Hungarian), statistics
C. 1585. What distinct positive primes \(\displaystyle p\) and \(\displaystyle q\) satisfy the equality \(\displaystyle p-4p^2+p^3=q-4q^2+q^3\)?
(5 pont)
solution (in Hungarian), statistics
C. 1586. The points \(\displaystyle D\) and \(\displaystyle E\) divide side \(\displaystyle AB\) of triangle \(\displaystyle ABC\) into three equal parts. Let \(\displaystyle P\) be an arbitrary interior point of line segment \(\displaystyle DE\). Draw parallels to line \(\displaystyle PC\) through the points \(\displaystyle D\) and \(\displaystyle E\). These lines intersect sides \(\displaystyle AC\) and \(\displaystyle BC\) at points \(\displaystyle Q\) and \(\displaystyle R\), respectively. Show that the area of quadrilateral \(\displaystyle PRCQ\) equals the area of triangle \(\displaystyle APQ\).
Proposed by B. Bíró, Eger
(5 pont)
solution (in Hungarian), statistics
C. 1587. Solve the equation
\(\displaystyle \frac{x-1}{\sqrt x}-\frac{\sqrt x}{x-2}=\frac{\sqrt x}{2x-1} \)
over the set of real numbers.
Proposed by B. Bíró, Eger
(5 pont)
 |
Problems with sign 'B'Deadline expired on February 10, 2020. |
B. 5070. There are two kinds of people living on an island: some always tell the truth, while some always lie. Ten inhabitants of the island were numbered as \(\displaystyle 1,2,\ldots,10\). Then everyone was asked the same three questions: ``Is your number even?'', ``Is your number divisible by 4?'', ``Is your number divisible by 5?''. The number of those saying ``Yes'' was three, six, and two, respectively in the three cases. Which numbers were assigned to liars?
Proposed by S. Róka, Nyíregyháza
(4 pont)
solution (in Hungarian), statistics
B. 5071. Let us consider a triangle \(\displaystyle ABC\). Let \(\displaystyle A_1\) and \(\displaystyle A_2\) denote the points that divide side \(\displaystyle BC\) into three equal parts, with \(\displaystyle A_1\) lying closer to vertex \(\displaystyle B\). Analogously, let \(\displaystyle B_1\), \(\displaystyle B_2\) divide side \(\displaystyle CA\) into equal parts, with \(\displaystyle B_1\) lying closer to \(\displaystyle C\), and let \(\displaystyle C_1\) és \(\displaystyle C_2\) divide \(\displaystyle AB\) into three equal parts, with \(\displaystyle C_1\) lying closer to \(\displaystyle B\). Prove that the triangles \(\displaystyle A_1B_1C_1\) and \(\displaystyle B_2C_2A_2\) are congruent, and both of their areas are equal to the third of the area of the triangle \(\displaystyle ABC\).
Proposed by B. Bíró, Eger
(3 pont)
solution (in Hungarian), statistics
B. 5072. Prove that \(\displaystyle \big[\sqrt n+\sqrt{n+3}\,\big]=\big[\sqrt{4n+5}\,\big]\) for all positive integers \(\displaystyle n\).
Proposed by T. Imre, Marosvásárhely
(3 pont)
solution (in Hungarian), statistics
B. 5073. The tangents drawn to the incircle of triangle \(\displaystyle ABC\), parallel to the sides, cut off three small triangles at the corners. The radii of the incircles of the small triangles are 2, 3 and 10 units long. Show that triangle \(\displaystyle ABC\) is right-angled.
Proposed by S. Róka, Nyíregyháza
(4 pont)
solution (in Hungarian), statistics
B. 5074. Find all positive integers \(\displaystyle n\) and distinct (positive) primes \(\displaystyle p\), \(\displaystyle q\), \(\displaystyle r\) for which
\(\displaystyle \frac1{pq}+\frac1{pr^3}+\frac1{qr^2}=\frac1n. \)
Proposed by G. Holló, Budapest
(5 pont)
solution (in Hungarian), statistics
B. 5075. The midpoints of sides \(\displaystyle AD\) and \(\displaystyle BC\) of a convex quadrilateral \(\displaystyle ABCD\) are \(\displaystyle E\) and \(\displaystyle F\), respectively. Line segment \(\displaystyle EF\) intersects diagonal \(\displaystyle AC\) at point \(\displaystyle P\), and diagonal \(\displaystyle BD\) at point \(\displaystyle Q\). Prove that the circles \(\displaystyle AEP\) and \(\displaystyle BFQ\) intersect each other on the line \(\displaystyle AB\).
Proposed by G. Holló, Budapest
(5 pont)
solution (in Hungarian), statistics
B. 5076. Find the real solutions of the system
$$\begin{align*} x+y+z+v & =0, \\ x^2+y^2+z^2+v^2 & = 12, \\ x^3+y^3+z^3+v^3 & = 24. \end{align*}$$(6 pont)
solution (in Hungarian), statistics
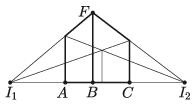
B. 5077. We want to draw a perspective image of a cube, using two vanishing points: \(\displaystyle I_1=(-9;0)\) and \(\displaystyle I_2=(10;0)\), as shown in the figure. The images of three vertices are \(\displaystyle A=(-3;0)\), \(\displaystyle B=(0;0)\) és \(\displaystyle C=(4;0)\). What should the \(\displaystyle y\)-coordinate of point \(\displaystyle F\) be?
(6 pont)
 |
Problems with sign 'A'Deadline expired on February 10, 2020. |
A. 767. In an \(\displaystyle n\times n\) array all the fields are colored with a different color. In one move one can choose a row, move all the fields one place to the right, and move the last field (from the right) to the leftmost field of the row; or one can choose a column, move all the fields one place downwards, and move the field at the bottom of the column to the top field of the same column. For what values of \(\displaystyle n\) is it possible to reach any arrangement of the \(\displaystyle n\) fields using these kinds of steps?
Proposed by Ádám Schweitzer
(7 pont)
A. 768. Let \(\displaystyle S\) be a shape in the plane which is obtained as a union of finitely many unit squares. Prove that the ratio of the perimeter and the area of \(\displaystyle S\) is at most 8.
(7 pont)
Upload your solutions above.
