A KöMaL 2021. januári matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2021. február 15-én LEJÁRT. |
K. 679. Peti még 3 éves korában kapta meg hat darabból álló építőjátékát, melyben minden építőelem téglatest alakú. Az elemek mérete \(\displaystyle 1~ \mathrm{dm} \times 1~ \mathrm{dm} \times 2~ \mathrm{dm}\). A tartódoboz belső mérete \(\displaystyle 3~ \mathrm{dm} \times 2~ \mathrm{dm} \times 2~ \mathrm{dm}\) és minden oldala más színű. Hányféle különböző elrendezésben pakolhatja be Peti a hat elemet a dobozába, ha az építőelemek ugyanolyan színűek és nem különböztetjük meg őket? (A dobozból nem lóghat ki egy építőelem sem.)
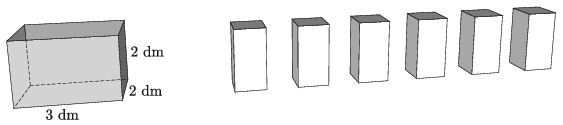
(6 pont)
K. 680. Egy kocka négy lapját befestettük pirosra, majd a kockát szétvágtuk 125 darab egyforma kiskockára. Ezek között hány olyan lehet, amelynek egyik lapja sem festékes?
(6 pont)
K. 681. Határozzuk meg, hány olyan háromszög van, melyben az oldalak hossza centiméterben mérve egész szám, és a leghosszabb oldala 2021 cm hosszú (lehet több ilyen oldala is).
(6 pont)
K. 682. Háromféle különböző számkártyánk van, mindegyikből elegendően sok. A számkártyákon egy-egy számjegy van. Ezekből a számkártyákból elkészítjük az összes lehetséges különböző pozitív négyjegyű számot. Ezeknek a négyjegyű számoknak az összege \(\displaystyle 689\,931\). Melyik az a három számjegy, ami a számkártyákon szerepel?
(6 pont)
K. 683. A körbe írható \(\displaystyle ABCDEFG\) hétszögben az \(\displaystyle ABC\sphericalangle\), \(\displaystyle CDE\sphericalangle\) és \(\displaystyle EFG\sphericalangle\) szögek összege nagyobb \(\displaystyle 450^{\circ}\)-nál. Mutassuk meg, hogy a köré írt kör középpontja nem lehet sem a hétszögön belül, sem annak valamelyik oldalán.
(The University of Stirling, school mathematics competition, 1983)
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2021. február 15-én LEJÁRT. |
C. 1644. Egy keskeny, \(\displaystyle 10 \mathrm{cm} \times 30 \mathrm{cm}\) méretű, téglalap alakú tepsiben sütit sütöttünk, melynek a széle lett a legropogósabb. A sütit úgy vágjuk fel, hogy a vágások az oldalakkal párhuzamosan, végig futnak. Hány darabra osztható a sütemény, ha azt szeretnénk, hogy minden darabon ugyanakkora rész legyen a ropogós széléből?
(5 pont)
C. 1645. Egy hegyesszögű háromszögben – a szokásos jelöléseket használva – \(\displaystyle m_b\), \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) ebben a sorrendben egymás utáni pozitív egész számok. Mekkora a háromszög területe?
Javasolta: Tatár Zsuzsanna Mária (Esztergom)
(5 pont)
C. 1646. Oldjuk meg az \(\displaystyle {(xy-1)}^2 = {(x + 1)}^2 + {(y + 1)}^2\) egyenletet az egész számpárok halmazán.
Javasolta: Szalai Máté (Szeged)
(5 pont)
C. 1647. Egy egyenlő szárú háromszög száraihoz tartozó súlyvonalak merőlegesek egymásra. Jelölje \(\displaystyle r\) és \(\displaystyle R\) a háromszög beírt és körülírt körének sugarát. Határozzuk meg az \(\displaystyle \frac{r}{R}\) arány pontos értékét.
(5 pont)
C. 1648. Arthur király és Sir Lancelot gyalog-galopp versenyt rendeznek. Sir Lancelot azt mondja Arthur királynak: ,,Felség, az ön gyalog-galopp sebessége az enyémnek csak a \(\displaystyle \frac{2}{3}\)-a, ezért adok önnek \(\displaystyle 100\) méter előnyt és a kijelölt versenypálya hosszán belül biztosan utolérem. Ha pedig ön \(\displaystyle 2 \frac{\mathrm{m}}{\mathrm{s}}\)-mal csökkentené a sebességét, én pedig \(\displaystyle 5 \frac{\mathrm{m}}{\mathrm{s}}\)-mal és \(\displaystyle 50\) méter előnyt adnék önnek, akkor is utolérném a pályán. A kétféle utolérési időtartam összege éppen \(\displaystyle 75\) másodperc.'' Határozzuk meg Arthur király és Sir Lancelot gyalog-galopp sebességét.
(5 pont)
C. 1649. Egy húrnégyszög átlói merőlegesen metszik egymást az \(\displaystyle M\) pontban. Az átlók a négyszöget háromszögekre bontják. Bizonyítsuk be, hogy bármelyik háromszög \(\displaystyle M\)-ből induló magasságvonala és a szemközti háromszög \(\displaystyle M\)-hez tartozó súlyvonala egy egyenesre esik.
(5 pont)
C. 1650. Igazoljuk az alábbi egyenlőtlenséget, ahol \(\displaystyle a, b, c>1\):
\(\displaystyle \log_{ab}c\le \frac{\log_ac + \log_bc}{4}. \)
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2021. február 15-én LEJÁRT. |
B. 5142. Egy focibajnokság egy csoportjában négy csapat szerepelt. A csoportban mindenki mindenkivel egyszer játszott. Győzelemért 3, döntetlenért 1, vereségért 0 pont járt. A két legtöbb pontot összegyűjtő csapat továbbjutott, a másik kettő kiesett. Pontegyenlőség esetén sorsolással döntöttek. Melyek azok a \(\displaystyle p\) számok, amelyekre előfordulhat, hogy egy továbbjutónak és egy kiesőnek egyaránt \(\displaystyle p\) pontja lett?
(3 pont)
B. 5143. Oldjuk meg a \(\displaystyle 16x^2+9x+117=24x\sqrt{x+13}\) egyenletet a valós számok körében.
Javasolta: Róka Sándor (Nyíregyháza)
(4 pont)
B. 5144. Az \(\displaystyle ABCD\) konvex négyszög területe \(\displaystyle t\), egy belső pontja \(\displaystyle O\). Mutassuk meg, hogy
\(\displaystyle 2t\le OA^2+OB^2+OC^2+OD^2. \)
Mikor áll fenn egyenlőség?
(3 pont)
B. 5145. Mutassuk meg, hogy azoknak az \(\displaystyle n\) hosszúságú nullákból és egyesekből álló sorozatoknak a száma, amelyekben pontosan \(\displaystyle k\)-szor fordul elő, hogy \(\displaystyle 0\) után \(\displaystyle 1\) következik, éppen \(\displaystyle \binom{n+1}{2k+1}\).
(Angol olimpiai válogatóverseny feladata)
(4 pont)
B. 5146. Adott egy egységnyi térfogatú \(\displaystyle T\) téglatest, és belsejében egy \(\displaystyle M\) pont. Tükrözzük az \(\displaystyle M\) pontot a téglatest lapsíkjaira, a kapott \(\displaystyle 6\) képpont konvex burka legyen \(\displaystyle D\). Határozzuk meg a \(\displaystyle T\cap D\) test térfogatát.
(5 pont)
B. 5147. Legyen \(\displaystyle k>1\) pozitív egész szám. Megadható-e a pozitív egészek olyan
\(\displaystyle a)\) tetszőlegesen nagy, véges
\(\displaystyle b)\) végtelen
részhalmaza, melyben bármely \(\displaystyle k\) elem legnagyobb közös osztója 1-nél nagyobb, továbbá bármely \(\displaystyle k+1\) elem legnagyobb közös osztója 1?
Javasolta: Mészáros Gábor (Budapest)
(5 pont)
B. 5148. Az \(\displaystyle ABC\) háromszögnek \(\displaystyle C\)-nél derékszöge van. A háromszögbe írt kör a \(\displaystyle BC\) befogót a \(\displaystyle D\), az \(\displaystyle AC\) befogót az \(\displaystyle E\) pontban érinti. A \(\displaystyle BC\) oldalhoz hozzáírt kör a \(\displaystyle BC\) szakaszt a \(\displaystyle G\) pontban érinti; hasonlóan, az \(\displaystyle AC\) oldalhoz hozzáírt kör az \(\displaystyle AC\) szakaszt a \(\displaystyle H\) pontban érinti. A \(\displaystyle DH\) és \(\displaystyle EG\) szakaszok metszéspontja \(\displaystyle M\). Mutassuk meg, hogy a \(\displaystyle DGM\) és az \(\displaystyle EHM\) háromszögek köré írt körök \(\displaystyle M\)-től különböző metszéspontja a beírt körre esik.
(6 pont)
B. 5149. Hányféleképpen lehet kitölteni egy \(\displaystyle 6\times 6\)-os táblázat mezőit az \(\displaystyle 1,2,\dots,36\) számokkal úgy, hogy bárhogy választunk 6 mezőt, melyek közül semelyik kettő nincs egy sorban vagy oszlopban, a kiválasztott mezőkbe írt számok összege mindig ugyanannyi legyen?
(6 pont)
 |
A-jelű feladatokA beküldési határidő 2021. február 15-én LEJÁRT. |
A. 791. Adva van egy villanykörte, amely piros, zöld vagy kék színnel tud világítani, és háromállású kapcsolók egy végtelen \(\displaystyle H\) halmaza, ahol mindegyik kapcsolónál meg van jelölve a három állás a piros, kék és zöld színekkel. A következőket tudjuk még:
\(\displaystyle i)\) Mindegyik kapcsolóállásnál egyértelműen meghatározott színnel világít a villanykörte.
\(\displaystyle ii)\) Ha mindegyik kapcsoló ugyanarra az adott színre van állítva, a villanykörte is az adott színnel világít.
\(\displaystyle iii)\) Ha két kapcsolóállásnál mindegyik kapcsolóra igaz, hogy különböző állásban van, akkor a két állásnál a villanykörte más színnel világít.
Készítsük el a \(\displaystyle H\) bizonyos részhalmazaiból álló \(\displaystyle U\) halmazt a következő módon: minden kapcsolóállásnál nézzük meg a villanykörte színét, és tegyük bele az \(\displaystyle U\) halmazba azon kapcsolók halmazát, melyek állása megegyezik a villanykörte színével.
Bizonyítsuk be, hogy \(\displaystyle U\) ultraszűrőt alkot \(\displaystyle H\)-n.
(\(\displaystyle U\) ultraszűrő \(\displaystyle H\)-n, ha teljesíti a következőket:
\(\displaystyle a)\) Az üres halmaz nincs benne \(\displaystyle U\)-ban.
\(\displaystyle b)\) Ha két halmaz benne van \(\displaystyle U\)-ban, a metszetük is benne van \(\displaystyle U\)-ban.
\(\displaystyle c)\) Ha egy halmaz benne van \(\displaystyle U\)-ban, minden nála bővebb \(\displaystyle H\)-beli részhalmaz is benne van \(\displaystyle U\)-ban.
\(\displaystyle d)\) Egy halmaz és \(\displaystyle H\)-beli komplementere közül pontosan az egyik van \(\displaystyle U\)-ban.)
Lásd még az N.\(\displaystyle \;\)35. feladatot az 1994-es évfolyam májusi számából. (Feladat és megoldás.)
(7 pont)
A. 792. Legyen \(\displaystyle p\ge 3\) prímszám és \(\displaystyle 0\le r\le p-3\). Legyen \(\displaystyle x_1, x_2, \ldots, x_{p-1+r}\) egész számok, melyekre \(\displaystyle \sum\limits_{j=1}^{p-1+r} x_j^k\equiv r~ \textrm{(mod}\ p\textrm{)}\) minden \(\displaystyle 1\le k\le p-2\)-re.
Mik lehetnek az \(\displaystyle x_1,x_2,\ldots ,x_{p-1+r}\) számok maradékai modulo \(\displaystyle p\)?
Javasolta: Matolcsi Dávid (Budapest)
(7 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

