A KöMaL 2021. februári matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2021. március 10-én LEJÁRT. |
K. 684. \(\displaystyle a)\) Zsófi és Balázs egy \(\displaystyle 10\times 5\) kockából álló csokit darabolnak fel, és közben egy játékot játszanak, melyben a tét három kocka csoki. A csokit felváltva törik el a kockákra osztó vonalak mentén, és az veszít a játékban, aki először tör le egy egy kockából álló darabot a csokiból. A játék során egyszerre csak egy darabot foghatnak meg, és törhetnek ketté a megadott szabály szerint. A játékot Zsófi kezdi. El tudja-e érni, hogy ő nyerjen?
\(\displaystyle b)\) Az első játék után Balázs visszavágót kért, azzal a feltétellel, hogy megint Zsófi kezdjen, de most az nyerjen, aki először tör egy egy kockából álló darabot. El tudja-e érni Zsófi, hogy ismét ő nyerjen?
(6 pont)
K. 685. Pisti elment gombát szedni. Mivel egyre gyakorlottabb, ezúttal 62 vargányát talált, így az elmúlt egy évben a gombagyűjtéseire vonatkozóan a megtalált vargányák átlagos darabszámát 30-ról 32-re emelte. Hány vargányát kellett volna találnia a legutolsó alkalommal, hogy az átlag 33-ra emelkedjen?
(6 pont)
K. 686. Felírjuk 1-től 100-ig az egész számokat egy-egy cédulára. A 100 darab cédula közül kiválasztunk véletlenszerűen 20 darabot. Mutassuk meg, hogy mindig találunk a kiválasztottak között négy olyat, hogy közülük kettőn-kettőn álló számok összege megegyezik.
(6 pont)
K. 687. Egy utca egyik oldalán áll valahány játékrobot. Egy lépésben pontosan négy robotnak tudunk parancsot adni, hogy menjen át az út túloldalára. Hány robot esetén lehet elérni, hogy a robotok az utca túloldalára kerüljenek át?
(6 pont)
K. 688. \(\displaystyle a)\) Párba lehet-e állítani az \(\displaystyle 1, 2, 3, 4, \ldots, 23, 24\) számokat úgy, hogy minden párban a számok összege négyzetszám legyen?
\(\displaystyle b)\) Párba lehet-e állítani az \(\displaystyle 1, 2, 3, 4, \ldots, 21, 22\) számokat úgy, hogy minden párban a számok összege négyzetszám legyen?
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2021. március 10-én LEJÁRT. |
C. 1651. Egy számsorozat tagjait a következő módon képezzük: a sorozat első tagja \(\displaystyle 895\), a következő tagot pedig mindig úgy kapjuk, hogy az előző tag számjegyeinek összegét megszorozzuk \(\displaystyle 61\)-gyel. Határozzuk meg a sorozat \(\displaystyle 2021\). tagját és az első \(\displaystyle 2021\) tag összegét.
(5 pont)
C. 1652. Két derékszögű háromszögnek egységnyi a rövidebb befogója. Mindkettő háromszögben a derékszögnél levő csúcs egységnyire van az átfogó harmadolópontjától: az egyik esetében a közelebbi, a másik esetében a távolabbi harmadolóponttól. Igazoljuk, hogy a háromszögek egységtől különböző oldalai között van három, amelyből derékszögű háromszög szerkeszthető.
(5 pont)
C. 1653. Hány megoldása van az egész számpárok körében az
\(\displaystyle |x|+|y|<2021 \)
egyenlőtlenségnek?
(5 pont)
C. 1654. Adjuk meg azoknak a köröknek a sugarát, amelyek érintik az \(\displaystyle f(x)=\frac{3x-6}{4}\) és a \(\displaystyle g(x)=\frac{28-4x}{3}\) függvények grafikonját, valamint az \(\displaystyle x\) tengelyt.
(5 pont)
C. 1655. Oldjuk meg a \(\displaystyle 2{(x+y-1831)}^2=(2x-1802)(2y-1860)\) egyenletet a valós számpárok halmazán.
(5 pont)
C. 1656. Egy számtani sorozat három szomszédos tagja 3-nál nagyobb prímszám. Mutassuk meg, hogy a sorozat differenciája osztható hárommal.
Javasolta: Németh László (Fonyód)
(5 pont)
C. 1657. Az \(\displaystyle ABC\) derékszögű háromszög \(\displaystyle BC\) és \(\displaystyle CA\) befogóira kifelé a \(\displaystyle BCD\) és \(\displaystyle CAE\) szabályos háromszögeket rajzoljuk. Bizonyítsuk be, hogy az \(\displaystyle AB\), \(\displaystyle CD\) és \(\displaystyle CE\) szakaszok felezőpontjai szabályos háromszöget alkotnak.
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2021. március 10-én LEJÁRT. |
B. 5150. Igazoljuk, hogy csak véges sok olyan pozitív egész szám van, amelyet nem lehet megkapni úgy, hogy egy kisebb számhoz hozzáadjuk annak valamelyik számjegyét. Melyik a legnagyobb ezek közül?
(4 pont)
B. 5151. Igazoljuk, hogy ha \(\displaystyle a^2=b^2+ac=c^2+ab\), akkor az \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) számok közül valamelyik kettő egyenlő.
(3 pont)
B. 5152. Határozzuk meg azokat az \(\displaystyle 1\)-nél nagyobb pozitív egész számokat, amelyek összes pozitív osztóját fel lehet írni egy körvonalra úgy, hogy a szomszédos osztók hányadosa mindig prímszám legyen.
Javasolta: Lenger Dániel (Budapest) és Szűcs Gábor (Szikszó)
(5 pont)
B. 5153. Legyenek \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) egy egységnyi oldalú szabályos háromszög csúcsai, míg \(\displaystyle D\) egy pont az \(\displaystyle AB\) oldal \(\displaystyle B\)-n túli meghosszabbításán. A \(\displaystyle BC\) szakaszra \(\displaystyle B\)-ben állított merőleges a \(\displaystyle CD\) szakaszt az \(\displaystyle E\) pontban metszi. Határozzuk meg a \(\displaystyle CE\) szakasz hosszát, ha \(\displaystyle ED=1\).
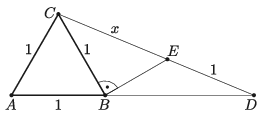
Javasolta: Szilassi Lajos és Tarcsay Tamás (Szeged)
(4 pont)
B. 5154. Adjuk meg az összes olyan pozitív egészeken értelmezett, pozitív egész értékű \(\displaystyle f\) függvényt, amelyre \(\displaystyle f\big(f(n)\big)=2n\) és \(\displaystyle f(4n-3)=4n-1\) teljesül bármely pozitív egész \(\displaystyle n\) esetén.
Javasolta: Róka Sándor (Nyíregyháza)
(4 pont)
B. 5155. Az \(\displaystyle ABCD\) konvex négyszögnek nincsenek párhuzamos oldalai, az \(\displaystyle AB\) és \(\displaystyle CD\) egyenesek metszéspontja \(\displaystyle M\). Az \(\displaystyle AB\) oldal belsejében az \(\displaystyle X\), a \(\displaystyle CD\) oldal belsejében pedig az \(\displaystyle Y\) pont úgy mozog, hogy közben \(\displaystyle AX:XB=DY:YC\). Mutassuk meg, hogy az \(\displaystyle MXY\) köröknek van még egy, \(\displaystyle M\)-től különböző közös pontja.
(5 pont)
B. 5156. Legyen \(\displaystyle K\) egy konvex \(\displaystyle 2n\)-szög, amelynek minden oldala egységnyi, és szemközti oldalai párhuzamosak. Mutassuk meg, hogy \(\displaystyle K\)-t fel lehet bontani véges sok egységnyi oldalhosszúságú rombuszra. Hány rombuszból állhat egy ilyen felbontás?
(6 pont)
B. 5157. A diákok a táblára felírtak néhány egész számot. Hárman (egymástól függetlenül) véletlenszerűen kiválasztanak egy-egy táblára írt számot, és leírják a füzetükbe. Mutassuk meg, hogy a három leírt szám összege legalább \(\displaystyle 1/4\) valószínűséggel 3-mal osztható.
(6 pont)
 |
A-jelű feladatokA beküldési határidő 2021. március 10-én LEJÁRT. |
A. 793. Adva van egy 43 dimenziós térbeli véges \(\displaystyle S\) ponthalmaz konvex burkában egy 47 csúcsú \(\displaystyle P\) poliéder. Mutassuk meg, hogy kiválaszthatjuk \(\displaystyle S\)-nek legfeljebb 2021 pontját úgy, hogy már az ő konvex burkukban is benne legyen \(\displaystyle P\), és ez éles.
Javasolta: Pálvölgyi Dömötör, Budapest
(7 pont)
A. 794. Egy négyzetrácson egy \(\displaystyle n\) darab négyzetből álló \(\displaystyle P\) poliminót egy lépésben fel lehet emelni a négyzetrácsról, és egy új pozícióba vissza lehet tenni (egy ilyen lépésnél minden egybevágósági transzformáció megengedett, amely a négyzetrácsot önmagába viszi), ha a régi és az új pozíció pontosan \(\displaystyle n-1\) darab közös egységnégyzetet tartalmaz. A \(\displaystyle P\) poliminóra azt mondjuk, hogy \(\displaystyle n\) területű pillangó, ha ilyen lépések sorozatával el lehet érni, hogy a \(\displaystyle P\) által eredetileg elfoglalt összes egységnégyzet felszabaduljon.
Hányféle nem egybevágó \(\displaystyle 10^6+1\) területű pillangót lehet találni?
Javasolta: Nikolai Beluhov, Bulgária
(7 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

