Fórum: A Goldbach-sejtésről

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50]

Szeretnél hozzászólni? Jelentkezz be.

[1146] Róbert Gida

2011-02-03 22:09:08

Szomorú. Tfel, hogy véges sok prím van: p₁=2,p₂=3,^...p_k, ekkor n-ig a p_i-khez relatív prímek száma logikai szitával:

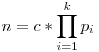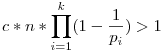$n-[\frac n2]-[\frac n3]-\cdots -[\frac {n}{p_k}]+[\frac {n}{2*3}]+[\frac {n}{2*5}]+\cdots +[\frac {n}{p_{k-1}*p_{k-2}}]\pm \cdots +(-1)^k[\frac {n}{2*3*\cdots *p_k}]$ . Ha $n=c*\prod_{i=1}^k p_i$ -t veszed (c egész), akkor az előbbi összeg: $c*n*\prod_{i=1}^k ({1-\frac {1}{p_i}})>1$ , ha c>1, így van a p_i-khez relatív prím egynél nagyobb egész, ami így csak prím lehet, ellentmondás.

Ez kb. az Eukleidesz bizonyítása csak logikai szitával elsütve. (Euler féle $\varphi$ fv-el is el lehetne mondani.)

Előzmény: [1143] bily71, 2011-02-03 21:48:41

[1145] Maga Péter	2011-02-03 21:59:09
Hopsz, csak most olvasom [1142]-t. Nem marad a lábjegyzet sem...
Előzmény: [1144] Maga Péter, 2011-02-03 21:55:52

[1144] Maga Péter

2011-02-03 21:55:52

,,Ha megengeded, akkor lehetne RGB tétel is a neve, mint Róbert Gida-Bily tétel. Elvégre én javasoltam a kiterjesztését a szitádnak.''

Ejjej..., ilyet nem illik. Bilyé az érdem, te csak azt vetted észre, hogy módszere lényegében változatlan formában működik az általánosabb kérdésben is. Ne aggódj, a neved így is fennmarad, amíg matematikával foglalkoznak a Világegyetemben (be kell érned a lábjegyzetekkel, de így is messze túlteszel a fórum összes többi látogatóján, Bilyt leszámítva).

Előzmény: [1140] Róbert Gida, 2011-02-03 21:18:33

[1143] bily71	2011-02-03 21:48:41
Nem.
Előzmény: [1141] Róbert Gida, 2011-02-03 21:20:00

[1142] bily71	2011-02-03 21:45:04
Elkéstél:) Már kb. féléve kiterjesztettem.
Előzmény: [1140] Róbert Gida, 2011-02-03 21:18:33

[1141] Róbert Gida	2011-02-03 21:20:00
Van egy érdekes másik problémám, igazolni tudnád a logikai szita módszerével, hogy végtelen sok prím van?
Előzmény: [1138] bily71, 2011-02-03 20:55:28

[1140] Róbert Gida

2011-02-03 21:18:33

"De te nem válaszoltál..."

Most válaszolok: nem értem, definíciókat az a,b sorozatokra még mindig nem látom.

"A szitamódszerem minden q=p+2k-ra működik (Polignac-sejtés),"

Nem, ha működik, akkor ez már tétel. Ha megengeded, akkor lehetne RGB tétel is a neve, mint Róbert Gida-Bily tétel. Elvégre én javasoltam a kiterjesztését a szitádnak.

Előzmény: [1138] bily71, 2011-02-03 20:55:28

[1139] Maga Péter	2011-02-03 20:57:12
Ez.
Előzmény: [1136] Zilberbach, 2011-02-03 20:48:57

[1138] bily71

2011-02-03 20:55:28

A szitamódszerem minden q=p+2k-ra működik (Polignac-sejtés), bármely k-ra "meg tudom számolni" az ilyen prímpárokat [x/6]-ig, mindegyiknél maradékosztályokat szitálok, gondolom nem nagy meglepetés, hogy ezeknél a szitáknál is a 6-os játsza a főszerepet. Ha a minoráns kritérium alkalmazható a k=1 esetben, vagyis az ikerprímes szitára, akkor minden k-ra alkalmazható.

De te nem válaszoltál...

Előzmény: [1134] Róbert Gida, 2011-02-03 20:35:59

[1137] Maga Péter	2011-02-03 20:54:55
Én nem.
Előzmény: [1133] bily71, 2011-02-03 20:34:21

[1136] Zilberbach	2011-02-03 20:48:57
Bocsánat, ha nagyon műveletlen vagyok, de mi az a GRH?
Előzmény: [1132] Róbert Gida, 2011-02-03 20:31:14

[1135] Zilberbach	2011-02-03 20:44:32
Köszönöm a kigazítást (Vinogradov) és a választ.
Előzmény: [1130] Maga Péter, 2011-02-03 20:21:04

[1134] Róbert Gida

2011-02-03 20:35:59

Ez telt 3 órába? Kicsit komplikált, de az ezúttal helyes bizonyításod. Azt meg tudnád mondani, hogy az általad használt minoráns kritériumos szitamódszered itt miért nem működik?

Van egy új sejtésem, ezúttal a többiek hozzászólását is várom:

Végtelen sok p prímre q=p+14 is prím! Be tudnád bizonyítani az ikerprímeknél használt módszerekkel ezt a sejtést?

Előzmény: [1131] bily71, 2011-02-03 20:30:39

[1133] bily71	2011-02-03 20:34:21
Péterhez és Róberthez: értitek a [1125]-ben leírtakat?

[1132] Róbert Gida	2011-02-03 20:31:14
Ami érdekes, hogy GRH mellett igazolták a ptlan Goldbach sejtést.
Előzmény: [1130] Maga Péter, 2011-02-03 20:21:04

[1131] bily71

2011-02-03 20:30:39

Megölsz a poénjaiddal...

Mivel 2-n kívül minden prím páratlan, így minden 17-nél nagyobb prím is az. Két páratlan prím különbsége csak páros lehet, itt a különbség pedig páratlan, ezért p csakis páros lehet, páros prím pedig csak egy van, ez a kettes, ebből következik, hogy legfeljebb egy p-re teljesülhet, tehát a sejtés nem igaz.

Előzmény: [1127] Róbert Gida, 2011-02-03 17:33:50

[1130] Maga Péter

2011-02-03 20:21:04

Nem Kolmogorov, hanem Vinogradov.

1. Nem. Jóval nagyobb korlátot ad, ami felett minden páratlan számra igaz az állítás. Ha jól tudom, mind a mai napig nem ellenőrizték le addig a korlátig.

2. Ha jól tudom, akkor az előállítások számára egy alsó becslést ad, ami (nagy számokra) jóval erősebb a konstans 3-nál, így garantál csupa páratlan prímekre történő felbontásokat is.

Előzmény: [1129] Zilberbach, 2011-02-03 20:14:51

[1129] Zilberbach

2011-02-03 20:14:51

Talán olvassa a fórumot olyan személy, aki ismeri annyira a páratlan Goldbach-sejtés bizonyítását, hogy választ tud adni az alábbi kérdésekre:

1. Bizonyítja-e Kolmogorov egyértelműen, hogy minden 7-nél nagyobb páratlan szám fölírható: (páratlan prím + páratlan prím + páratlan prím) alakban?

2. Vagy csak nagy általánosságban bizonyít, meghagyva azt az elvi lehetőséget, hogy egyes 7-nél nagyobb páratlan számoknál is lehetséges, hogy csak a (2 + 2 + páratlan prím) alakjuk esetére bizonyított a páratlan Goldbach-sejtés?

[1128] Fálesz Mihály	2011-02-03 18:55:08
Most már kötőjellel is. :-)
Előzmény: [1124] Kemény Legény, 2011-02-03 14:20:14

[1127] Róbert Gida	2011-02-03 17:33:50
Bilyhez: Végtelen sok p prímre p+17 is prím. Be tudnád látni ezt a sejtést is? (Kemény Legény, Péter, ne segítsetek!)
Előzmény: [1125] bily71, 2011-02-03 15:35:02

[1126] bily71	2011-02-03 16:40:57
Elírtam, a számlálókban valójában nem "-" hanem "+" van.
Előzmény: [1125] bily71, 2011-02-03 15:35:02

[1125] bily71

2011-02-03 15:35:02

Azért nem definiáltam még b_i-et, mert mint mondtam, az nem egy definíció, hanem több, méghozzá esetszétválasztással definiálható. [1084]-ben azt az esetet definiáltam, mikor a a_k=6k-1 alakú számtani sorozat k-adik tagja, (itt, a prímes szitában most csak a b₁-ket határozzuk meg, a b₂-ket majd akkor, ha a 6k+1 alakú számtani sorozatot szitáljuk, így lesz minden d-re két tag) azaz maga 6k-1 osztható 6u-1-gyel, ekkor, ha 6k-1 összetett, akkor b₁=29u, ha 6u-1 prím, akkor b₁=6u. A célom annak megmutatása, hogy b₁=c₁, b₂=c₂.

És hogy egyátalán mi szükség van a b_i tagokra? Ez egy korrekciós tag. Ha Például azt vizsgáljuk, hogy hány 5-tel osztható poz. egész van x-ig, akkor a válasz: [x/5]. Ha azt, hogy hány olyan tagja van az a₁=5, d=5 számtani sorozatnak, mely x-nél nem nagyobb, akkor a válasz ugyanaz. És ha mondjuk a₁=3, d=5? Akkor hány x-nél nem nagyob tag van? a válasz: [(x-3)/5]+1=[(x-3+5)5]=[(x+(5-3))/5], itt b=d-a₁=5-3, ezt az utolsót most érted?

Tehát p''(n)=p_n-p_n-1, vagyis direkte úgy definiáltam p''(n)-t (ez csak egy hülye jelölés, valahogy meg kell különböztetni a dolgokat, de már kifogytam a betűkből :D), hogy 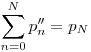$\sum_{n=0}^{N}p''_n=p_N$ , vagyis a sor N-edik részletösszege megegyezik a p_n sorozat N-edik tagjával, vagyis p_N-nel.

A p''(n) sorozat egy zárójelezése a következő p'''(n) sorozatnak:

$p'''_0=2\left[\frac{5^2}6\right]$

$p'''_1=-\sum_{i=1}^2\left[\frac{5^2-b_i}{6\cdot5}\right]$

$p'''_2=2\left[\frac{7^2}6\right]$

$p'''_3=-\sum_{i=1}^2\left[\frac{7^2-b_i}{6\cdot5}\right]$

$p'''_4=-\sum_{i=1}^2\left[\frac{7^2-b_i}{6\cdot7}\right]$

$p'''_5=\sum_{i=1}^2\left[\frac{7^2-b_i}{6\cdot5\cdot7}\right]$

$p'''_6=-2\left[\frac{5^2}6\right]$

$p'''_7=\sum_{i=1}^2\left[\frac{5^2-b_i}{6\cdot5}\right]$

$p'''_8=2\left[\frac{11^2}6\right]$

...

ugyanis

b''₀=b'''₀+b'''₁

b''₂=b'''₂+b'''₃+b'''₄+b'''₅+b'''₆+b'''₇

...

A p'''(n) sorozatot úgy kapjuk, hogy "felírjuk" a 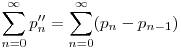$\sum_{n=0}^{\infty}p''_n=\sum_{n=0}^{\infty}(p_n-p_{n-1})$ végtelen sort és a $\mu(d)\sum_{i=1}^2\left[\frac{p_n^2+b_i}{6d}\right]$ tagokat megszámozzuk. Ennél jobb def. most hirtelen nem jut eszembe, de ha figyelmesen olvasod, akkor meg fogod érteni.

Kérlek, a következőket még figyelmesebben olvasd:

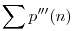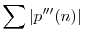Mivel konvergens sor bármely zárójelezése konvergens, és mivel a p''(n) sor divergens, (hiszen a 3-nál nagyobb prímek számát adja, melyekből végtelen sok van), de ez a p'''(n) sor zárójelezése, ezért kizárt, hogy p'''(n) konvergens legyen. Mivel $\sum{p'''(n)}$ divergens és $\forall$ n $\in$ N: p'''_n $\le$ |p'''_n|, ezért a $\sum{|p'''(n)|}$ is divergens. Legyen P_n=|p'''_n|, ekkor 0 $\le$ P_n $\le$ f'''_n, ezért f'''(n) is divergens. 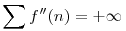Az f'''(n) sor az f''_n egy zárójelezése, ezért f''(n) nem lehet konvergens, következésképp $\sum{f''(n)}=+\infty$ . 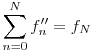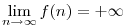Mivel $\sum_{n=0}^{N}f''_n=f_N$ , ezért $\lim_{n\to\infty}f(n)=+\infty$ , vagyis az ikerprímek száma végtelen.

Előzmény: [1122] Maga Péter, 2011-02-03 13:35:17

[1124] Kemény Legény	2011-02-03 14:20:14
Jó trükk. Próbáld kötőjellel is, azzal még csak 11.
Előzmény: [1123] Fálesz Mihály, 2011-02-03 14:09:24

[1123] Fálesz Mihály	2011-02-03 14:09:24
Bekerültünk az első tízbe. :-)
Előzmény: [1117] Róbert Gida, 2011-02-03 11:34:05

[1122] Maga Péter

2011-02-03 13:35:17

Most csak szívatsz... Eszem ágában nincs.

Olvasd már el könyörgöm az [1105]-t, ne csak RG vicces beszólásait! Megtettem. Persze előtte is elolvastam az [1100]-at, mert az viszonylag érthetően volt leírva, nem számítva azokat a dolgokat, amiket nem definiáltál (mint azóta már észrevetted, az [1084]-ben sem). Az [1105]-ről ez már nem mondható el: egy nagy halom számolás, nekem nem világos, hogy készül el például a p''-ből a p'''.

A másik, ha nem érted a következő definíciót, akkor egyátalán hogy lehetsz matematikus?! Ez a kérdés bennem is sokszor felmerül, csak a 'ha' után mást szoktam gondolni. Nemt'om, tanultam egy csomót, zh-kat írtam, vizsgáztam, néhol talán szerencsém is volt... mindazonáltal nem tartom magam matematikusnak abban az értelemben, ahogyan egy-egy nagy elődről szoktunk beszélni. Nekem csak papírom van róla, ami pontosan annyit jelent, hogy megkaptam azt a papírt. Ettől még van egy csomó matematikai definíció, fogalom, tétel, amit nem vagyok képes megérteni. Köztük olyan is, ami másoknak egyszerű. Ne lepődj meg, hogy te most találtál egy ilyet. A szándék, hidd el, nem hiányzik: vagy a magyarázat, vagy az én képességeim minősége a hibás.

Előzmény: [1120] bily71, 2011-02-03 12:49:33

Már regisztráltál?
Új vendég vagy?