| [177] bily71 | 2009-06-18 07:54:27 |
 Egyébként itt egy példa:
x=2 mod5
x=5 mod7
x=1 mod11
X=12 mod13
x=12 mod17...
Láthatjuk, hogy 12 kogruens 12-vel modulo összes p-ben, ha p prím nagyobb 12-nél, és ezzel VÉGTELEN sok feltételnek tesz eleget. Mivel a, b, c... számok tetszőlegesek, lehetnek azonos értékűek is.
Még mindig nem jól gondolom?
|
|
| [176] bily71 | 2009-06-17 22:13:02 |
 Szerintem a tétel igaz végtelen sok feltételre is. Ha lépésenként mindig csak eggyel növeljük a maradékosztályok számát, végül végtelen sok osztály lesz. A tétel nem szól arról hány osztály lehet.
Azt nem olvastad, hogy végtelen sok kombinációról beszéltem, és nem végtelen sok feltétel együtteséről?
A példa nem a legjobb, mert a táblázat 5-től kezdődik, és pl.: n nem lehet 4-gyel kongruens modulo ötben.
Én csak a számok egzisztenciáját akarom bizonyítani, a megnevezésüket másra hagyom. Euklidész sem tudott pár száznál, vagy pár ezernél több prímet megnevezni, mégis bebizonyította, hogy végtelen sok van.
Ha nem fogadnánk el, hogy véges sok lépésből egyszer végtelen sok lesz nem lenne integrál, limesz, vagy pl.: Taylor-sor.
Ez már elméleti kérdés. De lehet, hogy nincs igazam.
|
| Előzmény: [175] Sirpi, 2009-06-17 18:21:17 |
|
| [175] Sirpi | 2009-06-17 18:21:17 |
 Igen, de a kínai maradéktétel véges sok feltételről szól. Mivel garantálod, hogy ha végtelen sok feltételt írsz elő, akkor is kapsz olyan számot, ami minden kongruenciának megfelel?
Példa: mondj olyan pozitív egész n számot, amire teljesül, hogy
n 1mod 2 1mod 2
n 2mod 3 2mod 3
n 4mod 5 4mod 5
n 6mod 7 6mod 7
n 10mod 11 10mod 11
...
|
| Előzmény: [174] bily71, 2009-06-17 17:33:58 |
|
| [174] bily71 | 2009-06-17 17:33:58 |
 Tegyük félre egy kis időre a függvényt és az ábrákat. Találtam olyan tételt, ami leírja mire is gondoltam.
Az első sorban olyan számok vannak, amelyekre teljesül a következők egyike:
x=1 mod5
x=4 mod5.
(a = jel helyére három vonalat képzeljetek.) A második sorban a következők:
x=1 mod7
x=6 mod7.
A többi sorra is fel lehet írni ezeket a relációkat. Olyan számokat keresünk, amelyek nem ezeket a maradékokat adják. A kínai maradéktétel szerint mindig létezik olyan x, amelyre igaz a következő:
x=a mod5
x=b mod7
x=c mod11 ...
(a,b,c... tetszőleges egészek). Ha az a, b, c... számokat úgy választjuk meg, hogy ne a sorban lévő megoldásokat adja, mindig olya számot fogunk kapni, ami nem szerepel a mátrixban. Mivel az a, b, c... számokat végtelenféleképp variálhatjuk, végtelen sok olyan x-et kapunk, ami nem szerepel a mátrixban.
A KÍNAI MARADÉK TÉTEL SGÍTSÉGÉVEL VÉGTELEN SOK OLYAN SZÁM ÁLLÍTHATÓ ELŐ, AMIT NEM TARTALMAZ A VÉGTELEN NAGY IKERPRÍMES MÁTRIX.
Izgatottan várom a hozzászólásokat!
|
|
| [173] bily71 | 2009-06-16 20:44:16 |
 A mátrix első sorában minden szám öttel osztva négyet, vagy hatot ad maradékul. A második számai sor héttel osztva adják az első két szám valamelyikét maradékul. Ez minden sorra igaz.
Az első 2x2-es mátrixból az a szám marad ki, amelyik 5-tel osztva nem 4-et, vagy 6-ot, és héttel osztva nem 6-ot, vagy 8-at ad maradékul. A második mátrixban már négy szám osztási maradékait kell figyelembe venni. A harmadikban hatét, és így tovább.
Azt állítom, hogy MINDEN MÁTRIXBAN TUDUNK OLYAN SZÁMOT KONSTRUÁLNI, HOGY 5-TEL, 7-TEL, 11-GYEL... NEM A SOROK ELSŐ KÉT SZÁMÁT ADJA MARADÉKUL.
Ha valaki tud olyan tételt, ami szerint ez lehetetlen, akkor szóljon. Ha lehetséges ilyen számokat gyártani, akkor ezzel az egy mondattal bizonyítva van az ikerprím sejtés. Nekem mindig sikerült a kongruencia tulajdonságait kihasználva ilyen számokat létrehozni. Az ábrákat elküldöm Sirpinek. Peti sem tudta felrakni.
|
|
| [172] bily71 | 2009-06-16 13:05:20 |
 Azaz, mégiscsak van egy bizonyítási javaslatom, de nem tudom mennyire megalapozott matematikailag. Péternek elküldtem az ábrákat , hogy tegye fel. Ha fenn lesznek tényleg elkezdem a részletes levezetést.
|
|
| [171] bily71 | 2009-06-15 22:07:53 |
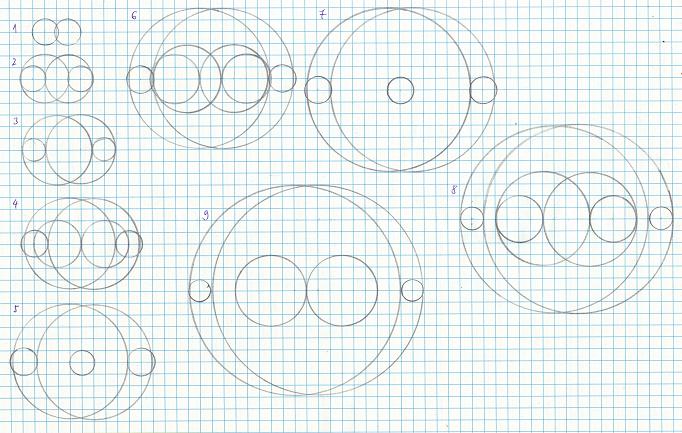
 A körök összevonásából a következő függvény jött ki:
(X-6nm)2+Y2=(n+-m)2, (a 2-esek hatványkitevők).
Az ábrát holnap felrakom. Ha ábrázoljuk a függvényt minden 6k körül koncentrikus körök lesznek. Az első két kör középpontja a 6-os, a sugarak pedig 0 és 2. A többi 6k köré rajzolt körök sugarai sorra: 1,3, 2,4 3,5... A sugarak különbsége mindig 2.
Ha k négyzetszám, akkor újabb körpárral kell számolni, a sugarak különbsége k négyzetgyökének kétszerese, és k-tól minden k négyzetgyök lépésre be kell rajzolni az új köröket. A körök sugara itt is minden lépésnél eggyel nő.
A függvény zérushelyei megegyeznek a mátrixban lévő számokkal.
Bevallom őszintén, megint elakadtam. Még nem találtam meg az általános szabályt, (csak azt hittem) hogy miért marad ki egy szám. Minden ujabb 2x2-es mátrixnál tovább bonyolódik a szabály. (Most az egyenletek komplex megoldásait vizsgálom, mert összefüggést találtam a zérushelyek eloszlásával kapcsolatban.)
Ha valaki tud segítsen. Azt kellene bizonyítani, ha lehet, hogy egy intervallumban nem lehet minden egésznél zérushely.
|
|
| [170] bily71 | 2009-06-14 13:55:44 |
 Igen, ez igaz, de könnyebb függvényből ábrát készíteni, mint ábrából függvény definiálni, és azt analizálni. Gőzerővel dolgozom. Azt hittem könnyebb lesz, nehéz megfogalmazni azt, ami nyílvánvaló. Főleg a matematika nyelvén.
|
| Előzmény: [169] Maga Péter, 2009-06-14 09:12:38 |
|
| [169] Maga Péter | 2009-06-14 09:12:38 |
 Izgatottan várom az ábrák formalizálását. Én értem, Bily, hogy mintákban akarsz gondolkodni, ennek erejét demonstrálandó említetted többek között a fraktálokat. Ha azonban a wikipedian rákeresel például a Cantor-halmazra vagy a Mandelbrot-halmazra, akkor azt tapasztalod, hogy egy jól meghatározott definíciójuk van, ami nem az, hogy "amit látsz az ábrán" (ti. vannak ábrák is). Kicsit esélyegyenlőségesebben fogalmazva (újabban ez nagy divat, asszem, függetlenül attól, hogy mikor mennyi értelme van:P): ne tiltsuk ki a vakokat a matematikából, márcsak Euler miatt sem.
|
|
| [168] bily71 | 2009-06-13 18:54:05 |
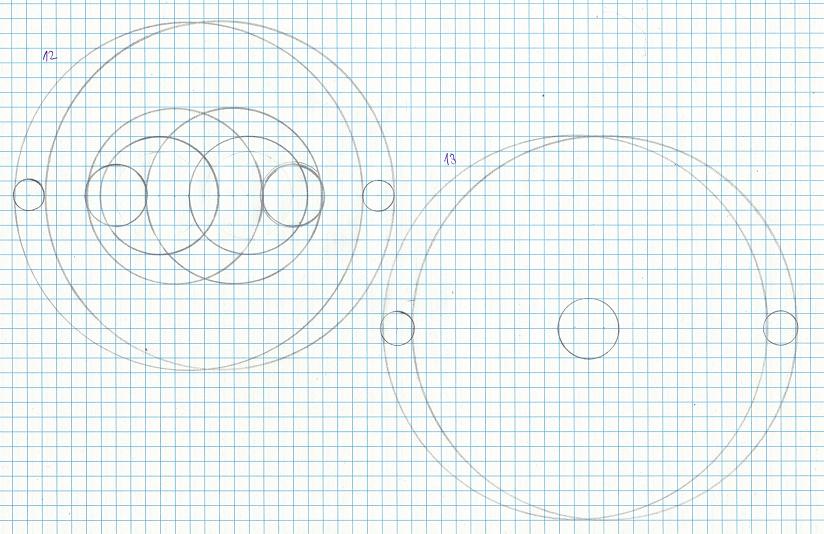
 Még egy ábrát felteszek. Sikerült még jobban egyszerűsítenem a függvényt. Az egymásba fonódott körök helyett rajzolhatunk koncentrikus köröket is. Mindeh 6 többszörös köré koncentrikus körök kerülnek.
Az is segítségünkre van, hogy minden 2x2-es mátrix számainak számtani közepe 6 többszöröse. A számtani közép értéke mindig az n és m szorzatának hatszorosa. A főátlóban lévő hat többszörösök köré így egy nulla sugarú kört is kell rajzolni.
Ma nincs időm, majd holnap folytatom.
|
|
| [167] bily71 | 2009-06-12 21:12:27 |
 A 2, 4 stb. sugarú körök minden második lépésben újabb intervallumokat nyitnak, ezek megfelenek a mátrix más 2x2-es celláinak. Ez a szimmetria nagyon megkönnyíti a vizsgálatot. A részletes levezetést holnap kezdem, ne várjatok bonyolult formulákat, eléggé triviális dolgokra fogok hivatkozni. Ma nem volt időm, három gyerek ugrál mindig körülöttem. A gép is szinte mindig foglalt.
|
|
| [166] bily71 | 2009-06-12 20:59:40 |
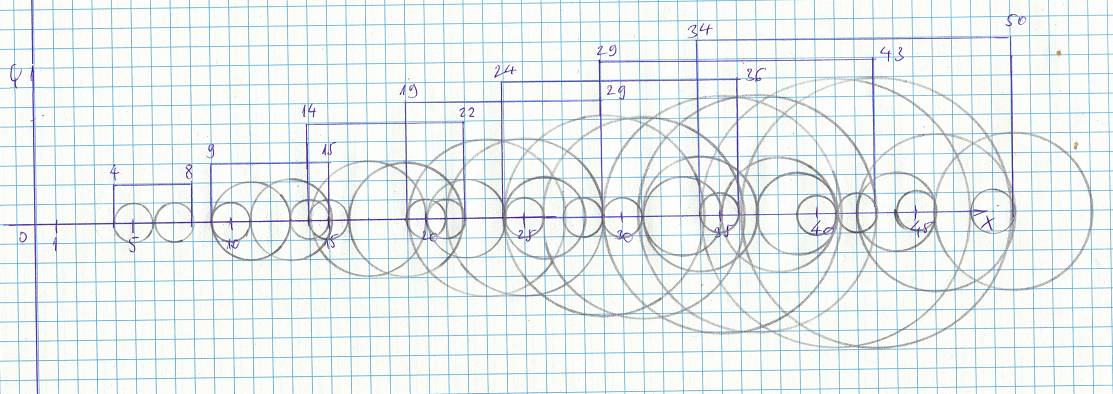
 Amint láthatjuk, minden intervallumban szimmetrikusan helyezkednek a körök. Minden intervallum 2m+2 hosszú.
A következő mintázatot fedeztem föl. Minden 5 többszörösnél kezdődik, és minden 7 többszörösnél végződik egy intervallum.
Ez törvényszerű, hiszen kommutatív félcsoport lévén a mátrix szimmetrikus. Minden n-dik lépéshez tartozó intervallum egyben az n=m-dik dupla vízszintes sor kezdete. Ebből következik, hogy a zérushelyek minden új körpárnál egybeesnek egy 5 és egy 7 többszörös köré rajzolt egy sugarú körök zérushelyeivel. Ebből következik az is, hogy az intervallumok átfedik egymást.
A kis körök úgymond széttolják az intervallumokat. Minden m sugarú kör ugyanilyen hatást indít el, mintha egy körhullám terjedne szét.
Minden máspdik lépésben nyomon követhető ahogy a kettő, majd a négy és így tovább, sugarú körök kezdik széttolni az ábrát.
Azt fogom felhasználni, hogy egy ilyen intervallumba csak meghatározott számú kör kerülhet, amiknek száma és sugara n--től függ. Ezek is csak bizonyos távolságokra. Pontosan meghatározható az is, hogy hány zérushely esik egybe a szimmetrikus elhelyezkedés miatt. Folyt. köv.
|
|
| [165] bily71 | 2009-06-12 20:20:27 |
 Megfogadom a tanácsod, már dolgozom rajta. Egyébként ez még mindig csak kisérlet. Lehet, hogy ez is csak egy zsákutca. Bár eléggé biztos vagyok, hogy valami érdekeset találtam, még ha nem is a teljes bizonyítást. Az én tudásom eltörpül sok fórumozóé mellett.
|
| Előzmény: [164] Huszár Kristóf, 2009-06-12 19:20:23 |
|
| [164] Huszár Kristóf | 2009-06-12 19:20:23 |
 Nagyon érdekes a téma, ami mostanában kezdett kibontakozni. Egy megjegyzésem van a dologgal kapcsolatban: Eléggé megnehezíti a bizonyítások vizsgálatát, hogy több tucat hozzászólásba szét vannak szórva a részletek. Számomra, és szerintem a többi fórumozó számára is nehezen érthető a gondolatmenet.
Sokkal áttekinthetőbb lenne, ha egy pdf dokumentumban az elejétől a végéig, logikusan felépítve le lenne írva, hivatkozásokkal, ábrákkal, és minden mással, ahogy ez egy tudományos munkához illik. Ez lehet, hogy időigényes, de hosszútávon megéri.
Kíváncsian várom a fejleményeket :-)
|
|
|
|
|
| [160] bily71 | 2009-06-12 16:33:36 |
 Egyébként nem olyan bonyolultak. Minden kört egy egyenlet ír le (lásd koordinátageometria, négyjegyű függvénytáblázat). y=0 esetben a két x érték paritása megegyezik, ezt kitudjuk használni. Ha egy másik körrel közös pontja van az x tengelyen, annak a paritása is szükségképpen megegyezik.
Az ábrákon szétszedtem az intrvallumokat. A lényeg az, hogy az egymásba csúszott intervallumok körei nem metszhetik minden egész számnál az x tengelyt.
Azt is vizsgálhatjuk, hogy hány szinuszhullámnak hány zérushelye található meg egy ilyen intervallumban, és ezekből hány esik egybe. Azt fogjuk találni, hogy nem lehet minden x zérushely.
|
| Előzmény: [158] Maga Péter, 2009-06-12 12:09:53 |
|
| [159] Sirpi | 2009-06-12 13:40:49 |
 Kaptam még 3 képet, pár óra múlva megpróbálom betenni, csak most durva alváshiányom van, szóval nem ígérem meg.
|
|
|
| [157] bily71 | 2009-06-11 14:39:04 |
 Az összes sorhoz rendelt sinushullámot egy koordináta rendszerben ábrázoltam, de nem eléggé áttekinthető, ezért rajzoltam köröket. Itt ebben a koordináta rendszerben az összes kör jelen van, csak azért nem tűnik úgy, mert azt elfelejtitek, hogy pl.: 31 többszöröse még nem jelenhet meg az első négy intervallumban. Szisztematikusan minden 6m+-1 alakú szám köré berajzoltam az m sugarú kört. Azt is elfelejtitek, hogy a kétdimenziós mátrix egy kommutatív félcsoport, a benne szereplő összes számot miért ne lehetne az egydimenziós számegyenesen ábrázolni? Hiszen komplex számokat nem tartalmaz. Hamarosan küldöm a többi ábrát, nagyon sok érdekes dologra fényt derítenek. Ha az egyenleteket vezetném le, nem lenne átlátható.
|
|
| [156] bily71 | 2009-06-11 12:32:17 |
 Vedd észre, hogy minden kör szükségszerűen megjelenik a számegyenesen, nemcsak az első két sor körei. És pont ez a lényeg. A körök és az x tengely metszéspontjai minden sorban lévő számot kijelöl. A mátrixban lévő minden szám megjeleníthető így egy intervallumon belül, attól függetlenül, hogy az első két sor 2x2 mátrixában szükségszerűen csak négy szám szerepel. Ha ez már érthető, elküldöm a többi ábrát.
|
| Előzmény: [155] Sirpi, 2009-06-11 10:25:37 |
|
|
|
| [153] bily71 | 2009-06-11 09:32:34 |
 Az első ábrát elküldtem Sirpinek és Maga Petinek. Nekem nem sikerült felrakni. Ha fel lesz téve, írom hozzá a magyrázatot. Lesz még két ábra.
|
|




 1mod 2
1mod 2