| [227] Maga Péter | 2009-06-21 14:00:26 |
 Valószínűleg messze nehezebb. El tudom képzelni, hogy ez (mármint a reciprokösszeg racionális volta) olyan kérdés, amire az emberiség soha nem fog tudni válaszolni. Az ikerprím-sejtés szerintem a következő 1000 évben megválaszoltatik:-).
|
| Előzmény: [222] Alma, 2009-06-20 15:30:05 |
|
| [226] bily71 | 2009-06-21 09:02:09 |
 Vagyis nem juthat minden prímre ikerprím index, igazad van.
|
|
| [225] bily71 | 2009-06-21 00:44:08 |
 Igen, most már látom, de a mátrix sorai nem feltétlenül prímek többszörösei, +- valamennyi, hanem vannak köztük összetett számok is, akár több is egymás melett, így nem jutna minden szám, és rá a hatodik szám közé ikerprímindex, ha feltételeznénk, hogy minden prím sorra jut egy.
Ugyanis az összetett sorokat kiejtik a prímek, mert pl.: az ötödik sor mod25-ben ugyanazt a kongruenciákat adja, mint az első sor számai mod5-ben, így a feltétel megadásánál nem kell figyelembe venni őket.
A prímek között pedig szabálytalan hosszúságú hézagok vannak. Ha ezekbe kerül egy-egy ikerprímindex, attól még lehet konvergens az ikerprímek reciprokösszege.
Vagy így sem járható ez az út?
|
| Előzmény: [224] Sirpi, 2009-06-21 00:05:50 |
|
| [224] Sirpi | 2009-06-21 00:05:50 |
 A páros számok reciprokösszege szintén végtelen. A 2-hatványok reciprokösszege az, ami 1 (mármint ha az 1-et nem vesszük bele, különben 2).
Azt be lehet látni könnyen, hogy ha van egy an pozitív, monoton csökkenő sorozatunk, aminek az összege végtelen (pl. a prímek reciprokai), akkor tetszőleges m-re igaz, hogy az am,a2m,a3m... sorozat összege is végtelen.
Hiszen
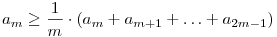
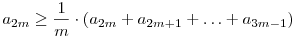
Általában
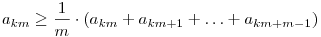
Innen:
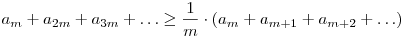 , és a jobb oldal a feltételek szerint végtelen, tehát a bal is. , és a jobb oldal a feltételek szerint végtelen, tehát a bal is.
Vagyis ha minden 6. (vagy akár csak minden milliomodik) prím ikerprím-pár egyik tagja lenne, akkor az ikerprímek reciprokösszege végtelen lenne, de tudjuk, hogy nem az.
|
| Előzmény: [223] bily71, 2009-06-20 22:23:19 |
|
| [223] bily71 | 2009-06-20 22:23:19 |
 Azt magyarázd el nekem, mert nem értem, hogy miért következik ez abból, hogy az ikerprímek reciprokösszege véges, a prímeké meg végtelen.
Hiszen a természetes számok reciprokösszege végtelen, a páros számoké pedig egyhez konvergál (lehet, hogy ezt sem tudom jól). Mégis mindkettő számossága megszámlálhatóan végtelen, holott legfeljebb kétszer annyi egész van, mint páros.
Egyébként ne higgyétek azt, hogy én akarom megmondani nektek mi a matematika, ellenkezőleg, rengeteget tanulok itt.
Ha nem mondom ki mire gondolok, megmaradok a tévhitemben. Azt is tudom, hogy sok badarságot összehordtam már itt, és még párszor nevetségessé fogom magam tenni. Kevesen játszanak úgy, mint Backham, de attól még milliók fociznak kedvtelésből.
|
| Előzmény: [206] Sirpi, 2009-06-19 23:04:40 |
|
|
| [221] bily71 | 2009-06-20 15:01:40 |
 Ok! Megint túl okosnak éreztem magam:P
De azt érdemes lenne megvizsgálni, hogy ha elhagyjuk az első két tagot, valóban irracionális lesz-e a reciprokösszeg.
|
|
|
|
|
|
| [216] jonas | 2009-06-20 13:25:08 |
 Várjál, mutatok egy példát. Vegyük az összes felső ikerprímet 7-től kezdve, úgy mint 7, 13, 19, 31, 43, 61, 73, ..., és írjuk fel őket 8-as számrendszerben: 7, 15, 23, 37, 53, 75, 111, 147, ..., írjuk a számjegyeket egymásután, nyolcas számrendszerben 0. 71523375375... (tízes számrendszerben 0.9009856...), ami pontosan 2011/2232, aminek a nevezője nem kettőhatvány, ezért ez nem véges nyolcados tört, tehát végtelen sok ikerprímszám van.
|
| Előzmény: [214] jonas, 2009-06-20 13:16:33 |
|
|
|
| [213] lgdt | 2009-06-20 13:13:34 |
 Nem egyenlő a kettő, hanem kb. 0.000047550514 a különbség köztük, de tényleg nagyon érdekes, hogy ennyire közel vannak. Én is tudok egy hasonlót: 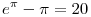 . :) . :)
|
| Előzmény: [210] bily71, 2009-06-20 12:09:37 |
|
| [212] bily71 | 2009-06-20 13:02:15 |
 Ha igazam van, akkor sétáljatok át velem az általam vert hídon, és nézzünk szét a matematika új világrészében.
Olyan összefüggéseket látok, ami engem is megdöbbent.
De ha tévedek, még egyszer elnézést kérek mindenkitől!
|
|
| [211] bily71 | 2009-06-20 12:52:46 |
 Elnézést kérek , még mindig nem tudod képleteket szerkeszteni a gépen, de fejben azért még megy.
Az ötszög átlójának hossza: gyök((5+gyök5)/2).
Az általam számitott konstans 6a/(6b+-1) alakú.
Tegyünk egyenlőségjelet a két szám közé. és vezessük le az egyenletet:
gyök((5+gyök5)/2)=6a/(ab+-1)
Előszőr is emeljünk négyzetre:
(5+gyök5)/2=6c/(6d+1).
Szorozzünk kettővel:
5+gyök5=6e/(6d+1).
Vegyünk el ötöt, azaz ((6-1)(6d+1))/(6e+1)-et:
gyök5=6f/(6d+1).
Emeljünk négyzetre:
5=6g/(6h+1).
Ami így is írható:
(6-1)=6g/(6h+1).
Szorozzunk (6h+1)-gyel:
(6-1)(6h+1)=6g.
Tehát egy azonosságot kaptunk a végére.
Ha nem jó, szóljatok!
|
|
| [210] bily71 | 2009-06-20 12:09:37 |
 Az egységnyi sugarú körbe írt szabályos ötszög hossza és az ikrerprímek reciprokainak összege (a 3,5 párt kihagyva ) MEGEGYEZIK!!!!!!!!!!!!!!!!
Márpedig az ötszög átlója irracionális... Azt, hogy mi következik ebből, már tudjátok.
Mindjárt küldöm a bizonyítást.
|
|
| [209] bily71 | 2009-06-20 11:30:56 |
 Ha már itt tartunk, szerintem ha a Brun számot úgy számoljuk ki, hogy kihagyjuk a 3,5 prímpárt, akkor az egységsugarú körbe írt szabályos ötszög átlójának hosszát kapjuk eredményül. De ez már egy másik komoly kérdéshez kapcsolódó bizonyítás lenne. Utána nézek, érdekes feladat.
|
|
| [208] Tibixe | 2009-06-20 11:28:02 |
 Ez nem jó módszer.
Nézzük az
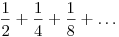
összeget.
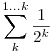
Az első n tagot összegezve és közös nevezőre hozva 2n-t kapunk nevezőnek és egy páratlan számot számlálónak, tehát semelyik részösszeg nem egyszerűsíthető.
Az összeg mégis egy racionális számhoz konvergál, nevezetesen az 1-hez :)
|
|
| [207] bily71 | 2009-06-20 11:12:20 |
 Pedig bizony, hogy meglehet csinálni...
Rájöttem, hogy mi lehet az a leküzdhetetlen akadály. 2300 évig a 3,5 prímpárt is az ikerprímek közé számították, holott nem áll elő 6k+-1 alakban, ezért szabálytalan ikerprím. Úgyanúgy kilóg az ikerprímek sorából, mint a 2-es a prímekéből, hiszen páros.
Ha a Brun konstanst úgy számoljuk ki, hogy nem vesszük bele a 3,5-ös párt, és csak a többi prímpár reciprokát adjuk össze, irracionális számot kapunk, ami azt jelenti, hogy az ikerprímek száma végtelen.
Hogy miért lesz irracionális? Az általános iskolából jól ismert az a módszer, ahogy összeadunk két törtet, egyszerűen közös nevezőre hozzuk. Ha sorra összeadjuk a reciprok értékeket, mindig új taggal növelve a sort, a számláló mindig 6-tal osztható, a nevező pedig mindig 6k+-1 alakú lesz. Így egyre nagyobb számok lesznek mind a nevezőben, mind a számlálóban, és akármennyi tagot adunk össze, soha nem tudunk egyszerűsíteni.
Na ezt add össze, de ha nincs igazam akkor elnézést kérek mindenkitől előre is:)
|
| Előzmény: [206] Sirpi, 2009-06-19 23:04:40 |
|
| [206] Sirpi | 2009-06-19 23:04:40 |
 Na, ez az, amit biztosan nem lehet megcsinálni. Ha igaz lenne, amit írsz, akkor legfeljebb hatszor annyi prím lenne, mint ikerprím, pedig az ismert tétel, hogy a prímek reciprokösszege végtelen, az ikerprímeké pedig véges.
|
| Előzmény: [205] bily71, 2009-06-19 21:43:06 |
|
|
| [204] Sirpi | 2009-06-19 21:12:21 |
 Figyelek én, csak már nem tudom, mire kell... Volt itt már 1, meg 2 egységgel növő négyzet, 2x2-es résztáblázatok, aztán kínai maradéktétel végtelen sok, majd később véges sok kongruenciára, és el tudom képzelni, hogy nem ez volt az utolsó kör.
Egyet értek Péterrel, kérünk egy állítást bizonyítással, aztán meglátjuk.
Egyébként egy kérdés a végére: pk-ig hány db. ikerprím-indexet garantálsz (aminek a 6-szorosa  1 prím)? Esetleg k-t (tehát minden új prímre egyet), vagy valamit félreértettem? 1 prím)? Esetleg k-t (tehát minden új prímre egyet), vagy valamit félreértettem?
|
| Előzmény: [202] bily71, 2009-06-19 18:43:38 |
|
| [203] Maga Péter | 2009-06-19 19:07:13 |
 Naaa...
Most már tényleg csináljuk úgy, hogy Bily szőröstül-bőröstül leírja az állítást és a bizonyítást! Majd azt megvitatjuk.
|
|









 1 prím)? Esetleg k-t (tehát minden új prímre egyet), vagy valamit félreértettem?
1 prím)? Esetleg k-t (tehát minden új prímre egyet), vagy valamit félreértettem?