|
| [81] SAMBUCA | 2005-02-18 15:17:54 |
 Helló!
Szerintem a feladat simán általánosítható n dimenzióra úgy, hogy a megfelelő méretű n-dimenziós kockát megfelelő méretű (n-1) dimenziós kockákkal fedjük le.
Ui. Kiváncsi lennék, hogy a megoldók hogyan oldották meg, de ezzel szerintem még várjunk 1-2 napot.
SAMBUCA (vajon ki???   ) )
|
| Előzmény: [80] Strenner Balázs, 2005-02-18 10:58:28 |
|
| [80] Strenner Balázs | 2005-02-18 10:58:28 |
 Nekem nagyon tetszett. Viszont érdekes, hogy általánosítható-e a feladat magasabb dimenziókra több kockával. Pl. n-dimnezióban n+1 kockával. Az érzésem az, hogy igen, de nem tudom biztosan. Aki tudja, megírhatja.
|
| Előzmény: [79] SAMBUCA, 2005-02-16 21:34:37 |
|
| [79] SAMBUCA | 2005-02-16 21:34:37 |
 Sziasztok!
Hogy tetszett az A pontversenyben a januári 2. feladat? :)
SAMBUCA
|
|
| [78] rizs | 2005-01-22 11:16:30 |
 a P.3735.-re godoltam :)
|
|
| [77] Pecu | 2005-01-14 14:26:57 |
 Sziasztok!
Az Iron által elkezdett hagyományt folytatva felírnám a P.3722. feladat eredményét. Ha jól emlékeszem közel 350 dolgozat érkezett, a fele lett három pontos, a másik fele pedig 0 pontos (szerintem ez lehet a másik feladat, aminek a statisztikája "megdöbbentő"), elvétve akadt csak 1 vagy 2 pontos. A baj az volt, hogy sokan azt írták, akkor lesz az A pont a súlypont, ha a háromszög és a négyzet területe megegyezik, mások pedig azt, ha a háromszög és a négyzet súlypontja egyenlő távolságra van az A ponttól. Ez pedig nem igaz, hiszen ha a két terület egyenlő, akkor a súlypontjuk nem egyenlő távolságra lesz A-tól, vagyis nem lesz 0 a forgatónyomaték, ugyanez a helyzet a másik esetben is. Szóval ezek a megoldások elvi hibásak, ezért a 0 pont. 1 vagy két pontot annak megfelelően adtam, hogy csak kisebb vagy komolyabb számolási hibák voltak a dolgozatban. A helyes megoldás az, ha a háromszög és a négyzet által az A pontra kifejtett forgatónyomatékok egyenlőségét vizsgáljuk, és a helyes b/a arány 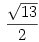 . Remélem ez így megfelel. . Remélem ez így megfelel.
Üdv, Pecu
|
|
| [76] rizs | 2005-01-12 23:48:42 |
 hasonlóan az említett p feladathoz, a k.11. statisztikája is elég megrázó. 6 pontos dolgozat lett? :)
|
|
| [75] eron | 2005-01-12 13:52:06 |
 Sziasztok! Ironnak sikerült olyan hosszú téli álmot aludnia, hogy elfelejtette a jelszavát, így eron néven született újjá.. Néhány lelkes kritikus jelezte, hogy jó lenne, ha a javítók közül, akinek van rá lehetősége, a dolgozatok lepontozása után az általa javított megoldások típushibáiról, és a jó megoldásról szólna néhány szót. El is kezdeném :) A P. 3725.-ös feladatra több mint 400-an küldtek megoldást, ebből 10 4-pontos, >200 3, >100 2, a többi 1 és 0, ez engem is feldühítene első ránézésre :). Az történt ugyanis, hogy az emberek elég nagy többsége a víz hőtágulását a megadott tartományban állandónak tekintette, ami a sűrűségértékeket megnézve nem teljesen igaz. Ha emellett minden jó, akkor kapott vki 3 pontot. Pontos eredmény úgy adódna, ha azt is beleszámolnánk, hogy a kifolyó víz sűrűsége, hőmérséklete, stb. nem állandó, ha a kifolyás folyamatával számolunk, akkor ez elég hosszadalmas; egészen egyszerűen fel lehet azt írni, hogy a 20 fokos vízsűrűséggel mekkora tömegű víz fér el az eredeti térfogatú bojlerbe, majd 80fokon, a már kitágult bojlerben (hiszen az is tágul, különben minek mondták volna meg, hogy acél?) mekkora tömegű a víz. A maradék tömeg nyilván kifolyik, ennek a térfogatát pedig lehet becsülgetni, de nem változtat sokat a végeredményen, hogy változik a hőmérséklete. Annak ellenére, hogy a víz hőtágulási együtthatójának a változása a megadott tartományban aránylag nem túl nagy, a fél literrel összehasonlítva számottevő különbség adódik: a "3 pontos" módszer a víz új térfogatára 0,68l körüli értéket ad, a valódi érték pedig (emlékeim szerint) 2,2l körül van, vagyis arányaiban nagy az eltérés. További pontlevonás: ha a tartály tágulásával nem foglalkozik vki, elszámolja, vagy elvi hiba.
Remélem, ez korrekt. Üdv: Áron
|
|
|
| [73] Strenner Balázs | 2004-11-11 09:30:40 |
 Kedves Géza!
Sokat gondolkoztam az A.344. feladaton, de végre sikerült találnom egy megolást. Remélem jó.
Tegyük fel, hogy van egy zárt hurok. A  hosszú oldalakat figyelmen kívül hagyva egy kígyószerű képződményt kapunk, aminek van egy belső határvonala (az ábrán piros), ami gráfos nyelven szólva nem tartalmazhat kört(mivel a hurok lyukmentes), tehát "fa". Ezért a fán haladva egyszer elérünk egy olyan rácspontba, amiből 3 irányba legfeljebb 1-1 ág indul, de összesen legalább 1. Vizsgáljuk ezeket a végződéseket. Az ábrán feltüntettem a szóba jövőket, ezek közül csak a bekarikázott lehetséges. Ekkor viszont a 3 csempét ki lehet cserélni 1-re, amivel rövidebb hurkot kapunk. És kész a végtelen leszállás. hosszú oldalakat figyelmen kívül hagyva egy kígyószerű képződményt kapunk, aminek van egy belső határvonala (az ábrán piros), ami gráfos nyelven szólva nem tartalmazhat kört(mivel a hurok lyukmentes), tehát "fa". Ezért a fán haladva egyszer elérünk egy olyan rácspontba, amiből 3 irányba legfeljebb 1-1 ág indul, de összesen legalább 1. Vizsgáljuk ezeket a végződéseket. Az ábrán feltüntettem a szóba jövőket, ezek közül csak a bekarikázott lehetséges. Ekkor viszont a 3 csempét ki lehet cserélni 1-re, amivel rövidebb hurkot kapunk. És kész a végtelen leszállás.
|
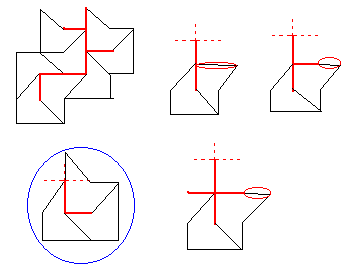 |
| Előzmény: [60] Kós Géza, 2004-06-04 10:25:03 |
|
| [72] jenei.attila | 2004-08-17 14:24:27 |
 Én is a rekurzió karakterisztikus egyenletéből kaptam a zárt alakot, amelynek komplex gyökei vannak, és a komplex számok hatványozására vonatkozó Moivre képletből (azt hiszem így hívják) adódik a zárt alak. Közvetlenül felismerni pedig szerintem nagyon nehéz lenne. A Csebisev polinomokkal való összefüggést esetleg észre lehet venni, de azok koszinuszos előállítását is ismerni kell.
|
| Előzmény: [71] Kós Géza, 2004-08-17 14:13:35 |
|
| [71] Kós Géza | 2004-08-17 14:13:35 |
 A nevezőből az következik, hogy an értéke sohasem lesz pontosan 1, mert soha sem lesz egész szám.
A koszinuszos alak nem igazán kerülhető ki. El lehet mondani persze a megoldást úgy, hogy csak titokban tudjuk, hogy koszinuszokról van szó, de az ugyanaz.
A kérdés inkább az, hogy mennyire lehet kitalálni a koszinuszos alakot. Aki nem ismeri fel közvetlenül, az még kezelheti a sorozatot lineáris rekurzív sorozatként is, abból is kiderül. De erről inkább valaki olyan nyilatkozzon, aki meg is oldotta a feladatot. :-)
|
| Előzmény: [70] jenei.attila, 2004-08-17 13:39:49 |
|
| [70] jenei.attila | 2004-08-17 13:39:49 |
 Igaz. Ezek szerint az an=cos(n*arccos(1/3)) összefüggésből azonnal következik a feladat állítása. Az igaz, hogy a rekurzióból kiolvasható hogy an nevezője 3n, de ebből hogyan következik a feladat állítása? Van -e olyan megoldás, ami nem használja fel a koszinuszos zárt alakot?
|
| Előzmény: [69] Kós Géza, 2004-08-17 12:57:07 |
|
| [69] Kós Géza | 2004-08-17 12:57:07 |
 Szia Attila,
A feladat megoldásához nem szükséges bebizonyítani, hogy 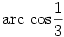 irracionális. Ha racionális lenne, akkor az (an) sorozatban végtelen sokszor szerepelne az 1, és az állítás akkor is igaz volna. irracionális. Ha racionális lenne, akkor az (an) sorozatban végtelen sokszor szerepelne az 1, és az állítás akkor is igaz volna.
Abban igazad van, hogy a Csebisev-polinomok egy kis kerülőt jelentenek. A rekurzióból --- ami a feladat szövegében is szerepelt --- közvetlenül kiolvasható, hogy an nevezője 3n.
|
| Előzmény: [68] jenei.attila, 2004-08-17 11:00:07 |
|
| [68] jenei.attila | 2004-08-17 11:00:07 |
 Szia Géza!
Bocs, előbb valami hiba történt.
Köszi a megoldást. Egyébként a B.3740-es feladatról volt szó, ugyanis az ott szereplő rekurzív sorozat zárt alakja: an=cos(n*arccos(1/3)). Mivel arccos(1/3) irracionális, ezért cos(n*arccos(1/3)) tetszőlegesen közel kerülhet 1-hez. Én is a csebisev polinomokra gondoltam, csak már nem emlékeztem rá, hogy a cos(n*arccos(x)) polinomban nem 1 -e a főegyüttható (de ezek szerint nem). Egyébként a feladat viszonylag ártalmatlannak néz ki ahhoz, hogy a Csebisev polinomokat kellene bevetni. Van ennek valami egyszerűbb megoldása is? Persze a rekurzióból leolvasható, hogy an=Tn(1/3), és esetleg meg sem kell említeni, hogy itt a Csebisev polinomokról van szó, mégis ha valaki nem ismeri, elég nehezen jön rá, hogy pont egy ilyen polinom sorozatot definiáljon.
|
| Előzmény: [66] Kós Géza, 2004-08-17 08:55:37 |
|
|
| [66] Kós Géza | 2004-08-17 08:55:37 |
 A 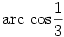 szám irracionális. szám irracionális.
Jelöljük az n-edik Csebisev polinomot Tn-nel; ez az a polinom, amelyre cos n =Tn(cos =Tn(cos  ). Például T0(x)=1, T1(x)=x, T2(x)=2x2-1, T3(x)=4x3-3x. ). Például T0(x)=1, T1(x)=x, T2(x)=2x2-1, T3(x)=4x3-3x.
A Tn polinomokra sok érdekes összefüggés ismert, például Tn+1(x)=2xTn(x)-Tn-1(x). Ebből a rekurzióból máris leolvasható az a két tulajdonság, amire most szükségünk lesz:
a) A Tn polinom pontosan n-edfokú és mindegyik együtthatója egész;
b) A fő együtthatója 2n-1.
Ha 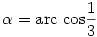 fokban kifejezve mégis racionális lenne, akkor lenne olyan n fokban kifejezve mégis racionális lenne, akkor lenne olyan n többszöröse, ami egész és még 360 fokkal is osztható. Erre az n számra legyen Tn(x)=2n-1xn+an-1xn-1+...+a1x+a0; ekkor többszöröse, ami egész és még 360 fokkal is osztható. Erre az n számra legyen Tn(x)=2n-1xn+an-1xn-1+...+a1x+a0; ekkor
3nTn(1/3)=Tn(cos  )=3ncos n )=3ncos n =3n, =3n,
2n-1+3an-1+9an-2+...+3na0=3n.
Minden tag osztható 3-mal, kivéve a 2n-1-t, ez pedig lehetetlen.
|
| Előzmény: [65] jenei.attila, 2004-08-16 17:33:56 |
|
| [65] jenei.attila | 2004-08-16 17:33:56 |
 Egy KÖMAL feladattal kapcsolatban merült fel a következő kérdés: vajon arccos(1/3) fokban kifejezve irracionális -e?
|
|
|
| [63] nadorp | 2004-06-30 07:48:30 |
 Sziasztok !
Ha valamilyen apró ötletet tudtok adni az A 348. feladathoz, azt nagyon megköszönném.
N.P.
|
|
| [62] Pach Péter Pál | 2004-06-09 22:27:45 |
 A B. 3699.-es feladat egyben a "Kavics Tanár Úr Pályázat" 2. feladata is volt. A lapban közölt megoldásnál szerintem elegánsabb megoldást olvashattok itt.
|
|
| [61] Hajba Károly | 2004-06-04 10:45:00 |
 Kedves Géza!
Túlzottan nem csodálkozom, hogy nem értesz mindent, mivel a fejemben sem állt még össze a kép teljesen, s a sok firkámat nem tudtam hirtelen feldolgozni, hogy érthetőbb legyen, amit gondoltam.
Hozzászólásodból kisejlik, hogyha jó is az elképzelésem, nagyon-nagyon izadtságszagú és lenne elegánsabb megoldás is.
Ha lesz egy kis időm, mindenképpen szeretnék még foglakozni vele.
Üdv: HK
|
| Előzmény: [60] Kós Géza, 2004-06-04 10:25:03 |
|
| [60] Kós Géza | 2004-06-04 10:25:03 |
 Őszintén szólva, nem minden részletet értek... :-)
Az viszont biztos, hogy félreérthetően fejezhettem ki magam korábban. Én lényegében két különböző megoldást ismerek. Az egyik megoldás közvetlenül, a hurkok átrendezése nélkül bizonyítja, hogy minden hurok belseje páratlan számú négyzetből áll.
A másik megoldás a végtelen leszállás; ez minden teljesen kitöltött hurokból konstruál egy még kisebbet. (Lehetséges, hogy a paritás is kiderül, ha a megoldást kicsit ügyesebben mondjuk el.)
* * *
A feladatot a versenyben összesen ketten oldották meg, mindketten a végtelen leszállást találták meg.
|
| Előzmény: [59] Hajba Károly, 2004-06-03 23:24:30 |
|
| [59] Hajba Károly | 2004-06-03 23:24:30 |
 Kedves Géza!
Míg ki nem hűl a forró nyom, folytatom. Tudom, még nem teljes, de leírom az újabb elgondolásomat, hogy legyen mire reagálva újabb információmorzsát adnod a továbblépésemhez. :o)
Ha a hurok rajzolatában találok két azonos törésvonalat úgy, hogy egy-egy törésvonal csak kétszer messe a hurkot, akkor a köztük levő idomokat és hiányokat kivéve egymáshoz illeszthetem, s egy rövidebb hurkot kapok. (Ha többször metszi, akkor az eljárás szükség szerint ismételhető.)
1) Ezen eltolás mindkét koordináta irányban csak páros lehet, mivel az azonos irányultságú idomhatároló szakaszok távolsága 2 egység többszöröse.
2) Az azonos állású szakaszok között páros számú elem lehetséges, mivel a vonallánc egyszer az egyik irányba, utána pedig a másik irányba dőlt szakaszon halad át.
3) (2)-ből következően a hurok hossza legalább 4, de mindenképpen páros egységgel csökken.
4) Két szabályosan egymáshoz illesztett idom azonos irányultságú szakaszainak felező pontjait összekötő vonal vízszintesen vagy függőlegesen két páratlan számosságú részre, míg ferdén két páros számosságú részre osztja.
5) A kivágott hurokszakasz és a törésvonalak közötti terület (1) miatt páros nagyságú; az összetartozó szakadási pontok közötti s ezzel a vonallal elvágott idomrészek területe páros (4) miatt. Így ha páros összterületből páros idomterületet levonunk, páros hiányterületet kell kapjunk.
Tehát, a fenti hurokhossz csökkentő módszerrel mindenképpen páros számmal csökken a bezárt hiány számossága.
Nos egyelőre ennyit, tudva, hogy ha ez is a jó megoldás, néhány részletet még ki kell zárni vagy megoldani.
HK
|
| Előzmény: [58] Kós Géza, 2004-06-02 21:45:38 |
|
|




 )
)



 =Tn(cos
=Tn(cos 
 an, akkor feltehetjük, hogy ezen az A halmazon
an, akkor feltehetjük, hogy ezen az A halmazon 
