Fórum: nem euklideszi geometria

Szeretnél hozzászólni? Jelentkezz be.

2013-04-03 14:16:40

Korrekcióra van szükség. Képletek elején hibásan adtam meg az y-t.

y=x²+4a²b²

Tehát az alkalmazni kívánt két függvény definíciója így nézne ki:

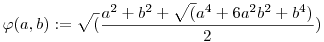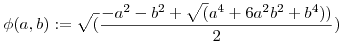
$\varphi(a,b):=\sqrt(\frac{a^2+b^2+\sqrt(a^4+6a^2b^2+b^4)}2)$ , $\phi(a,b):=\sqrt(\frac{-a^2-b^2+\sqrt(a^4+6a^2b^2+b^4))}2)$

Még olyan tétellel nem találkoztam, hogy az állandó szögösszegű háromszögekkel rendelkező geometriai struktúrák halmaza egyelemű és az csakis az Euklideszi geometria lehet. És ez a szögösszeg csakis a $\pi$ , se több, se kevesebb nem lehet. Eddig nem találkoztam ellentmondással, hacsak az nem, hogy előjön az a bizonyos defektus, ami pedig a nem euklideszi geometriák egyik tulajdonsága. Annak bizonyítása sincs meg, hogy az általam felvázolt struktúra ténylegesen állandó szögösszegű háromszögekből áll.

Előzmény: [65] gyula60, 2013-04-02 20:49:07

[66] Fálesz Mihály

2013-04-02 22:49:08

Csak ismételni tudom magamat.

Ha van hasonlóság, és a hasonló háromszögeknek ugyanakkorák a szögeik, akkor vagy euklideszi geometriáról van szó, vagy pedig a képletek ellentmondanak, és ilyen geometriai struktúra nincs.

Előzmény: [65] gyula60, 2013-04-02 20:49:07

[65] gyula60

2013-04-02 20:49:07

A derékszögű háromszögek esetén szintén felállíthatónak tűnt a magasság-tétel és befogó-tételek megfelelői, csak vigyázni kell az átfogóval, mert az illesztés során egy d defektust szenved m²/c értékkel. Itt előjött két kétváltozós függvény:

Legyen x=a²+b², és y=x²+4ab,

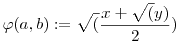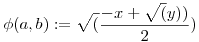$\varphi(a,b):=\sqrt(\frac{x+\sqrt(y)}2)$ , $\phi(a,b):=\sqrt(\frac{-x+\sqrt(y))}2)$ ,

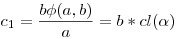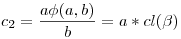
$c_1=\frac{b\phi(a,b)}a=b*cl(\alpha)$ , $c_2=\frac{a\phi(a,b)}b=a*cl(\beta)$

/c1 és c2 a befogók vetületei az átfogó "egyenesén"/

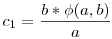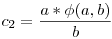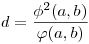$\varphi$ (a,b)=c, $c_1=\frac{b*\phi(a,b)}a$ , $c_2=\frac{a*\phi(a,b)}b$ , $d=\frac{\phi^2(a,b)}{\varphi(a,b)}$ , c=c₁+c₂+d,

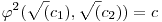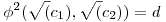$\varphi^2(\sqrt(c_1),\sqrt(c_2))=c$ , $\phi^2(\sqrt(c_1),\sqrt(c_2))=d$ , $\phi$ (a,b)=m, mc=ab= $\varphi$ (a,b) $\phi$ (a,b),

A fentiekből még két érdekes függvényegyenlet is felírható: 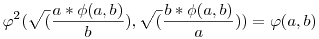$\varphi^2(\sqrt(\frac{a*\phi(a,b)}b), \sqrt(\frac{b*\phi(a,b)}a))=\varphi(a,b)$ ,

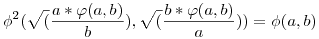$\phi^2(\sqrt(\frac{a*\varphi(a,b)}b), \sqrt(\frac{b*\varphi(a,b)}a))=\phi(a,b)$ .

Az itt bemutatott defektus ellenére bizonyítani kellene, hogy a két trigonometria között milyen fajta kapcsolat létesíthető.

Előzmény: [64] Fálesz Mihály, 2013-04-02 14:23:28

[64] Fálesz Mihály	2013-04-02 14:23:28
Ha van hasonlóság, ráadásul a háromszögek szögösszege mindig ugyannyi, akkor a geometria csak euklideszi lehet.
Előzmény: [63] gyula60, 2013-04-02 00:14:21

[63] gyula60

2013-04-02 00:14:21

Szeretnék ismertetni egy nem-euklideszi trigonometriát. A dolog teljesen intuitív módszerekkel történt és egy kis nem-euklideszi trigonometriás tapasztalattal. Algebrai és intuitív módszerekkel az elliptikus függvényekből levezethető lemniszkáta cl(x) és sl(x) függvények segítségével hoztam létre a konstrukciót. Ugyanúgy, ahogy a klasszikus trigonometrikus függvények szintén periodikusak és a félperiódus nem $\pi$ , hanem (saját jelölés) $\pi$ _m=2,62205... irracionális transzcendens szám. 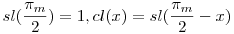A kiindulást jelentő függvények ugyanúgy folytonosak, korlátosak, differenciálhatók, mint a trigonometrikus társaik és cl(0)=1, sl(0)=0, cl(-x)=cl(x), sl(-x)=-sl(x), sl( $\pi$ _m)=0 $sl(\frac{\pi_m}2)=1, cl(x)=sl(\frac{\pi_m}2-x)$ stb.

Mindannyian rendelkeznek addíciós képlettel: 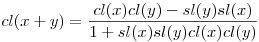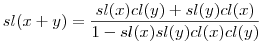$cl(x+y)=\frac{cl(x)cl(y)-sl(y)sl(x)}{1+sl(x)sl(y)cl(x)cl(y)}$ , $sl(x+y)=\frac{sl(x)cl(y)+sl(y)cl(x)}{1-sl(x)sl(y)cl(x)cl(y)}$ Összekötő egyenletük: cl²(x)+sl²(x)+cl²(x)sl²(x)=1 Az én intuícióm ennek nyomán feltételezett egy Pitagorasz-tételt ami így nézne ki: a²b²+c²(a²+b²)=c⁴, ahol a és b lenne a befogó és c az átfogó. 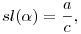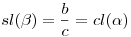Ezekben a derékszögű háromszögekben érvényesül a hasonlóság és $sl(\alpha)=\frac{a}c,$ $sl(\beta)=\frac{b}c=cl(\alpha)$ . 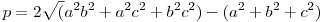A háromszög oldalai között értelmezni kell egy $p =2\sqrt(a^2b^2+a^2c^2+b^2c^2)-(a^2+b^2+c^2)$ mennyiséget és levezethetővé vált az általánosabb "háromszögre" egy koszinusztétel:

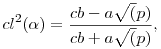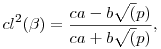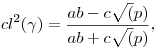
$cl^2(\alpha)=\frac{cb-a\sqrt(p)}{cb+a\sqrt(p)},$ $cl^2(\beta)=\frac{ca-b\sqrt(p)}{ca+b\sqrt(p)},$ $cl^2(\gamma)=\frac{ab-c\sqrt(p)}{ab+c\sqrt(p)},$

Majd ennek nyomán a szinusztétel is:

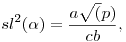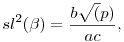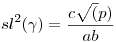
$sl^2(\alpha)=\frac{a\sqrt(p)}{cb},$ $sl^2(\beta)=\frac{b\sqrt(p)}{ac},$ $sl^2(\gamma)=\frac{c\sqrt(p)}{ab}$

Derékszögű háromszög esetén 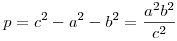$p=c^2-a^2-b^2=\frac{a^2b^2}{c^2}$ és így sl( $\gamma$ )=1, cl( $\gamma$ )=0. (ahol c az átfogó)

Még egy fontos sejtés: az "általános háromszög" szögeinek összege $\pi$ _m=2,62205... állandó és értelmezhetőnek tűnik a hasonlóság is.

[62] Sinobi	2013-03-18 22:26:27
Szerintem az ábra hasznosabb lenne, ha a gömbök metsznék egymást - arra úgy is szükség van metsző körök esetében, így egy eset elég lenne kettő helyett.
Előzmény: [61] Fálesz Mihály, 2013-02-07 14:04:20

[61] Fálesz Mihály	2013-02-07 14:04:20


Előzmény: [57] marcius8, 2013-02-01 15:56:31

[60] marcius8

2013-02-01 17:28:32

Elnézést kérek mindenkitől, az [57] hozzászólásomat pontosítom: Juliska három gyurmagolyóból összegyúrva egyetlen gyurmagolyót készít, a gyurmagolyók sugarai 16cm, 68cm, 88cm. Jancsi három gyurmagolyóból összegyúrva egyetlen gyurmagolyót készít, a gyurmagolyók sugarai 35cm, 70cm, 85cm. Kinek lesz nagyobb sugarú gyurmagolyója? A megoldáshoz fel kell használni, hogy az "r" sugarú gömb térfogata "lambda" paraméterű elliptikus térben: V=2*lambda*lambda*pi*r-lambda*lambda*lambda*pi*sin(2r/lambda), "lambda" paraméterű hiperbolikus térben: V=lambda*lambda*lambda*pi*sh(2r/lambda)-2*lambda*lambda*pi*r, euklideszi térben V=4*pi*r*r*r/3. (ez utóbbi képlet előáll a nem euklideszi esetekben felírt képletek határértékeként, ha lambda-->végtelen.)

[59] Lóczi Lajos	2013-02-01 16:48:13
Jancsinak lesz nem kisebb gyurmagolyója.
Előzmény: [57] marcius8, 2013-02-01 15:56:31

[58] marcius8

2013-02-01 16:14:46

Sok fizikai problémát is érdemes megvizsgálni euklideszi geometriában és nem euklideszi geometriában.

1. A fénytörés (Snellius-Descartes) törvény alakja tetszőleges geometriában ugyanúgy néz ki, ha elfogadjuk, hogy a Fermat-elv mindig érvényes. (Fermat-elv: a fény egy pontból egy másik pontba úgy igyekszik eljutni, hogy az út megtételéhez szükséges idő a lehető legrövidebb legyen. Fénytörés: Egy fény két közeg határfelületére érve úgy törik meg, hogy a fény beesési szögének szinuszának és a fény törési szögének szinuszának hányadosa mindig a két közegre jellemző mennyiség, az úgynevezett törésmutató.) Speciális esetként a vékony lencse (tükör) nevezetes sugármeneteit illetve a vékony lencse (tükör) leképezési törvényét is meg lehet vizsgálni.

2. Az "m" tömegű bolygó gravitációs terének vizsgálata. Ehhez szükséges tudni, hogy az "r" sugarú gömb felszíne "lambda" paraméterű hiperbolikus geometriában A=4*pi*lambda*lambda*sh(r/lambda)*sh(r/lambda), "lambda" paraméterű elliptikus geometriában A=4*pi*lambda*lambda*sin(r/lambda)*sin(r/lambda), euklideszi geometriában A=4*pi*r*r. Talán ennek a problémakör megoldásának ismeretében meg tudjuk-e állapítani a gravitációs térerősség mérésével, hogy milyen paraméterű és milyen geometriában vagyunk?

3. A speciális relativitás elve. A Lorentz transzformáció hogyan néz ki euklideszi geometriában illetve nem euklideszi geometriában?

4. Ez ugyan nem fizika, hanem szerkeszthetőség. Euklideszi geometriában a kör nem négyszögesíthető, a négyzet oldala és átlója nem összemérhető, a szabályos ötszög oldala és átlója nem összemérhető. Nem-euklideszi geometriában van négyszögesíthető kör, van olyan négyzet, amelynek oldala és átlója összemérhető, van olyan szabályos ötszög, amelynek oldala és átlója összemérhető.

[57] marcius8

2013-02-01 15:56:31

"FM" hozzászólónak: A feladatodra (egyenlőre) nem találtam olyan megoldást, amilyet szeretnél. Bár nem mindenki szereti a trigonometriát, különösképpen a nem-euklideszi síkbeli trigonometriát, de néhány érdekességet a teljesség igénye nélkül leírok, amelyet érdemes végiggondolni.

1. A húrnégyszögekre vonatkozó Ptolemaiosz-tételt (lásd korábbi hozzászólásomat) csak olyan húrnégyszögre igazoltam, amelynek csúcsai egy körön vannak. Érdemes kiszámolni az "a", "b", "c", "d" oldalú "s" félkerületű húrnégyszög köré írt kör sugarát és területét. Érdemes azt is végigszámolni, hogy az "a", "b", "c", "d" oldalú csuklós négyszögek közül melyiknek maximális a területe, eredményként az adódik, hogy ekkor annak a csuklós négyszögnek maximális a területe, amelyre teljesül a Ptolemaiosz-összefüggés.

Sok számolást lehetne még elvégezni, de ami a szemléletnek ellentmondani látszik, az a következő feladat: Jancsi három gyurmagolyóból összegyúrva egyetlen gyurmagolyót készít, a gyurmagolyók sugarai 16cm, 68cm, 88cm. Jancsi három gyurmagolyóból összegyúrva egyetlen gyurmagolyót készít, a gyurmagolyók sugarai 35cm, 70cm, 85cm. Kinek lesz nagyobb gyurmagolyója? A megoldáshoz fel kell használni, hogy az "r" sugarú gömb térfogata "lambda" paraméterű elliptikus térben: V=2*lambda*lambda*pi*r-lambda*lambda*lambda*pi*sin(2r/lambda), "lambda" paraméterű hiperbolikus térben: V=lambda*lambda*lambda*pi*sh(2r/lambda)-2*lambda*lambda*pi*r, euklideszi térben V=4*pi*r*r*r/3. (ez utóbbi képlet előáll a nem euklideszi esetekben felírt képletek határértékeként, ha lambda-->végtelen.)

[56] Fálesz Mihály

2013-01-30 13:55:04

Én nem a Ptolemaiosz-tétellel folyatnám (a képleteidet nem ellenőriztem), és a nemeuklideszi trigonometria sem okoz túl nagy esztétikai élményt.

Nézzük inkább két kör hatványvonalát. A feladat a következő:

Adott (egyelőre az euklideszi) síkban két körvonal, k₁ és k₂, mondjuk egymáson kívül. Egy P pontot nevezzzünk érdekesnek, ha P-ből ugyanolyan hosszú érintő szakaszt lehet húzni k₁-hez és k₂-höz. Az iskolában tanultuk, hogy az érdekes pontok egy egyenesen vannak. A kérdés az, hogy miért vannak egy egyenesen.

Az kevés, hogy számolással ellenőrizhetjük. Olyan bizonyítást keressünk, amiből közvetlenül, számolás nélkül derül ki, hogy a hatványvonal tényleg egy egyenes.

Előzmény: [52] marcius8, 2013-01-30 12:48:36

[55] Fálesz Mihály

2013-01-30 13:27:13

OK.

(Én továbbra is úgy szeretem jobban kimondani, hogy a csúcsok egy cikluson vannak, ahol a "ciklus"-ba beleértem a kört, a para/horociklust és a hiperciklust is.)

Előzmény: [54] marcius8, 2013-01-30 13:15:25

[54] marcius8	2013-01-30 13:15:25
Csakugyan van olyan négyszög a hiperbolikus geometriában melynek két szemközti szögének az összege egyenlő a másik két szemközti szögének összegével, ugyanakkor a négyszög csúcsai nincsennek egy körön, ennek oka, hogy ebben az esetben a négszög oldalfelező merőlegesei nem metszik egymást. Köszönöm az észrevételt, erre a következőkben is oda fogok figyelni. Akkor nagy hirtelen pontosítok a tételen: Egy konvex négyszög oldalfelező merőlegesei pontosan akkor tartoznak ahhoz a sugársorhoz, ha a konvex négyszög két szemközti szögének összege egyenlő a konvex négyszög másik két szemközti szögének az összegével. Ha a konvex négyszög oldalfelező merőlegesei egy pontban metszik egymást, akkor a négyszög csúcsai egy körön találhatóak, tehát a négyszög klasszikus értelemben is húrnégyszög.
Előzmény: [53] Fálesz Mihály, 2013-01-30 13:04:21

[53] Fálesz Mihály

2013-01-30 13:04:21

"A húrnégyszöget úgy értelmezem (...), hogy olyan négyszög, amelynek minden csúcsa ugyanazon a körön(!!!) van."

Ebben az esetben az állításod nem igaz. Hiperbolikus geometriában van olyan ABCD négyszög, amiben A $\angle$ +C $\angle$ =B $\angle$ +D $\angle$ , a csúcsok még sincsenek egy körön. (Sőt, semelyik három csúcs nincs egy körön...)

Előzmény: [52] marcius8, 2013-01-30 12:48:36

[52] marcius8

2013-01-30 12:48:36

"FM" hozzászólónak: A húrnégyszöget úgy értelmezem (euklideszi geometriában és nem euklideszi geometriában egyformán), hogy olyan négyszög, amelynek minden csúcsa ugyanazon a körön(!!!) van. Esetleg még érdemes átgondolni, hogy tetszőleges geometriában a húrnégyszögekre vonatkozó Ptolemaiosz-tétel hogyan fogalmazható meg, vagy tetszőleges geometriában a húrnégyszög területe hogyan határozható meg a húrnégyszög négy oldalának ismeretében.

Pl. Ptolemaiosz-tétel: Legyen "a", "b", "c", "d" a húrnégyszög négy oldala ebben a sorrendben, és legyen "e", "f" a húrnégyszög két átlója.

Euklideszi geometria: e*f=a*c+b*d

"lambda" paraméterű elliptikus geometria:

sin(e/(2*lambda))*sin(f/(2*lambda))=sin(a/(2*lambda))*sin(c/(2*lambda))+sin(b/(2*lambda))*sin(d/(2*lambda))

"lambda" paraméterű hiperbolikus geometria:

sh(e/(2*lambda))*sh(f/(2*lambda))=sh(a/(2*lambda))*sh(c/(2*lambda))+sh(b/(2*lambda))*sh(d/(2*lambda))

Érdemes észrevenni, hogy ha "lambda"-->végtelen, akkor az elliptikus geometria és a hiperbolikus geometria tart az euklideszi geometriához, és ekkor a nem-euklideszi geometriában kimondott Ptolemaiosz-tételek tartanak az euklideszi geometriában kimondott Ptolemaiosz-tételhez.

[51] Fálesz Mihály

2013-01-28 13:56:59

Ha a hiperbolikus síkot a projektív síkba (elliptikus geometriába) ágyazzuk be a Klein-modellel, akkor egy görbének látszanak.

Ha viszont a hiperbolikus síkot az inverzív síkba (gömbi geometriába) ágyazzuk be valamelyik Poincaré-modellel, akkor különböző görbének látszanak.

Előzmény: [47] Vonka Vilmos Úr, 2013-01-28 12:23:00

[50] Fálesz Mihály	2013-01-28 13:42:45
A kérdés nem a bizonyításra irányult, hanem elsősorban a "húrnégyszög" fogalmának tisztázására.
Előzmény: [48] marcius8, 2013-01-28 13:29:25

[49] Vonka Vilmos Úr

2013-01-28 13:40:19

A húrnégyszögek tételének ez a hiperbolikus általánosa igen szép (és úgy látom, elég friss) eredmény (én legalábbis 2009-es és 2011-es hivatkozásokat találtam rá).

Tisztázni kell azonban előtte, hogy mit is értünk a hiperbolikus síkon húrnégyszögön. Ahhoz, hogy ilyen tételt fogalmazhassunk meg, a húrnégyszögeket a következő módon érdemes definiálni: olyan négyszög, amelynek csúcsai egy körre, horociklusra, vagy egy ekvidisztáns görbe egy ágára illeszkednek.

Előzmény: [48] marcius8, 2013-01-28 13:29:25

[48] marcius8

2013-01-28 13:29:25

Sokan hivatkoznak a CK-modellre, ami nem baj. De szerintem az igazi nem-euklideszi geometria az, ha a tételeket közvetlenül, nem pedig modell alapján bizonyítjuk, azaz mintha nem-euklideszi síkra születtünk volna.

Más: Korábbi hozzászóló kérdezte a húrnégyszögek tételét: tetszőleges geometriában egy négyszög pontosan akkor húrnégyszög, ha a négyszög két szemközti szögének az össszege egyenleő a négyszög másik két szemközti szögének összegével. Euklideszi geometriában ennél több is igaz: Egy négyszög pontosan akkor húrnégyszög, ha a négyszög két szemközti szögének az összege 180° és a négyszög másik két szemközti szögének az összege 180°. Ennek bizonyítását nem írom ide, de ha az említett hozzászóló kéri, elküldöm e-mail-ben a tétel bizonyítását.

Bertalan Zoltán (marcius8)

[47] Vonka Vilmos Úr	2013-01-28 12:23:00
Persze, az a Klein-modellben is látszik, hogy a szóban forgó ekvidisztáns görbéknek két ága van, hiszen van két "végtelen távoli pontjuk".
Előzmény: [45] Fálesz Mihály, 2013-01-28 12:10:16

[46] jonas	2013-01-28 12:10:39
Ja értem! Három olyan ekvidisztáns görbe van, aminek a két ágán együtt van rajta a három csúcs.
Előzmény: [44] Vonka Vilmos Úr, 2013-01-28 11:35:06

[45] Fálesz Mihály

2013-01-28 12:10:16

Nekem azért fenntartásaim vannak ezzel.

Arról van ugye szó, hogy az egyenes két oldalán két, állandó görbületű görbét (távolsággörbe, hiperciklus stb.) alkotnak azok a pontok, amik az egyenestől adott távolságra vannak. Ha akarjuk, és a Klein/modellben nézzük, akkor ez a két görbe valójában egy, hasonlóan az euklieszi hiperbola két ágához. Ha viszont valamelyik Poincaré/modellben nézzük, akkor kiderül, hogy két látványosan különböző görbéről van szó. A félgöbbmodell mutatja legjobban, hogy mi az oka ennek a kettősségnek. Ezt majd lerajzolom.

* * *

De mindez csak a lényegről elterelő mellékszál, és kb. annak a kérdésnek felel meg, hogy a euklideszi háromszög köré írt kört általánosítja-e az a három párhuzamos egyenespár, ami szintén tartalmazza-e a csúcsokat.

Inkább térjünk vissza a kérdéshez: láttuk, hogy minden háromszög köré írható egy állandó görbületű, összefüggő görbe, ami lehet kör, vagy paraciklus (angolban ikább horociklusnak nevezik), vagy hiperciklus. Kérdés a topiknyitóhoz: Hogy is volt az a dolog a húrnégyszögekkel?

Előzmény: [44] Vonka Vilmos Úr, 2013-01-28 11:35:06

[44] Vonka Vilmos Úr

2013-01-28 11:35:06

A hiperbolikus háromszög mindhárom középvonala egy-egy ilyen ekvidisztáns görbe tengelye. (Ennek a ténynek a megfelelője az euklideszi síkon is igaz: mindegyik oldalegyenes és a szemköztes csúcson át azzal húzott párhuzamos, mint párhuzamos egyenespár, egy ilyen ekvidisztáns görbe.)

A bizonyítás elemi úton pl. Coxeter Non-Euclidean Geometry c. könyvében megtalálható (9.67.). Érdekes az előző hozzászólásomban említett projektív megközelítés is: például ebben a jegyzetben a 144. oldalon található meg három pontra illeszkedő, adott kúpszeletet kettősen érintő kúpszelet szerkesztése. Ha a k kúpszelet a Klein-modell határköre, akkor éppen a hiperbolikus sík adott háromszöge köré írt ekvidisztáns görbe meghatározását jelenti a feladat. A jegyzet ábráján adódó X és Y pontok ekkor pontosan a megfelelő háromszögoldalak felezőpontjai (a hiperbolikus felezőpont a modellben ugyanis éppen egy olyan pontpár belső eleme, ami konjugált a határkörre nézve és harmonikusan választja el a szakasz végpontjait). Tehát a jegyzetben olvasható szerkesztés éppen azt mutatja, hogy a középvonalak mindig egy-egy megfelelő ekvidisztáns görbe tengelyei. A negyedik ekvidisztáns görbe pedig pontosan akkor jön létre, ha az ábrán szereplő X'Y' szakasz metszi a modellkört. Mivel X'Y' éppen a felezőmerőlegesek által alkotott sugársor tartópontjának polárisa, ez pontosan akkor igaz, ha a felezőmerőlegesek közös pontja "kívül esik a hiperbolikus síkon" - tehát ha a háromszög köré nem írható kör.

Előzmény: [43] jonas, 2013-01-28 10:16:28

[43] jonas	2013-01-28 10:16:28
Ebből a három ekvidisztáns görbét nem értem. Én azt hittem, hogy mindig csak nulla vagy egy ekvidisztáns görbe lehet, ami a háromszög három csúcsán átmegy.
Előzmény: [42] Vonka Vilmos Úr, 2013-01-26 16:39:52

[1] [2] [3] [4]

Már regisztráltál?
Új vendég vagy?