|
| [17] emm | 2015-05-24 00:26:20 |
 Mivel a Fibonacci-spirál logaritmikus spirál, ezért a paraméterezése:
&tex;\displaystyle x(\theta)=a\cos \theta e^{b\theta}\qquad y(\theta)=a\sin \theta e^{b\theta}\qquad z(\theta)&xet;
Az egyenletesen emelkedve (nekem legalábbis) azt jelenti, hogy "megtett ívhossz=konstans&tex;\displaystyle \cdot&xet;emelkedés"
&tex;\displaystyle \int_{\theta_1}^{\theta_2}\sqrt{\left(\frac{\partial x(\theta)}{\partial \theta}\right)^2+\left(\frac{\partial y(\theta)}{\partial \theta}\right)^2+\left(\frac{\partial z(\theta)}{\partial \theta}\right)^2}{\rm{d}}\theta=c\left(z(\theta_2)-z(\theta_1)\right)&xet;
Legyen &tex;\displaystyle w(\theta)=\frac{\partial z(\theta)}{\partial \theta}&xet;, és végezzük el a zárójelen belüli egyszerűsítéseket:
&tex;\displaystyle \int_{\theta_1}^{\theta_2}\sqrt{a^2(1+b^2)e^{2b\theta}+w(\theta)^2}{\rm d}\theta=c\int_{\theta_1}^{\theta_2}w(\theta){\rm d}\theta&xet;
Vagyis elegendő azt biztosítani, hogy:
&tex;\displaystyle a^2(1+b^2)e^{2b\theta}+w(\theta)^2=c^2w(\theta)^2&xet;
Ebből:
&tex;\displaystyle w(\theta)=\frac{a\sqrt{(1+b^2)}e^{b\theta}}{\sqrt{c^2-1}}\implies z(\theta)=\frac{a\sqrt{(1+b^2)}e^{b\theta}}{b\sqrt{c^2-1}}&xet;
(Azért, hogy &tex;\displaystyle \theta=-\infty&xet;-ben &tex;\displaystyle 0&xet; magasan legyünk). Vagyis a görbe paraméterezése:
&tex;\displaystyle x(\theta)=a\cos \theta e^{b\theta}\qquad y(\theta)=a\sin \theta e^{b\theta}\qquad z(\theta)=\frac{a\sqrt{(1+b^2)}e^{b\theta}}{b\sqrt{c^2-1}}&xet;
Mivel forgásszimmetrikus a &tex;\displaystyle z&xet; tengelyre, ezért a teljes felület paraméterezése:
&tex;\displaystyle
\left( a e^{b \theta } \cos (\theta +\omega ), \qquad
a e^{b \theta } \sin (\theta +\omega ), \qquad
\frac{a \sqrt{b^2+1} e^{b \theta }}{b \sqrt{c^2-1}}
\right)
&xet;
Ahol &tex;\displaystyle a\in R^+&xet; (lényegtelen) skálázási paraméter, &tex;\displaystyle b=\frac{2}{\pi}&xet;ln&tex;\displaystyle \varphi&xet;, ahol &tex;\displaystyle \varphi=\frac{1+\sqrt{5}}{2}&xet;, &tex;\displaystyle c>1&xet; tetszőleges.
|
| Előzmény: [16] lorantfy, 2015-05-23 23:00:45 |
|
| [16] lorantfy | 2015-05-23 23:00:45 |
 Jó ez a Fibonacci körút! Az jutott eszembe, hogy milyen z(x) függvény írja le azt a hengerszimmetrikus dombot, amire a Fibonacci spirál mentén egyenletesen emelkedve mehetünk fel?
|
|
| [15] Hajba Károly | 2015-05-19 20:02:49 |
 Valószínű nem lesz valami népszerű ez az óra. :o)
Egy kis segítség: öt perc pontossággal jelzi az időt, s a fehér semleges szín.
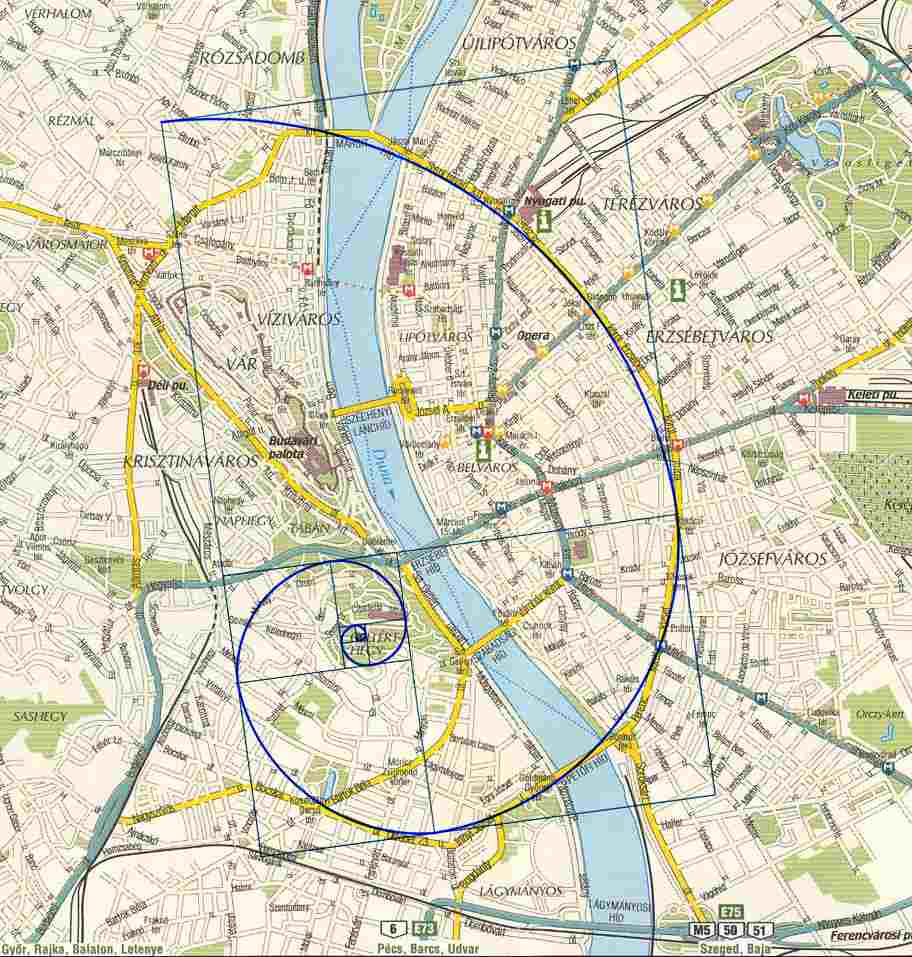
Persze Rodolfo-t játszottam, s ezért engesztelésül berakok egy Finonacci érdekességet. Budapesten a Fibonacci körutat.
|
 |
| Előzmény: [14] lorantfy, 2015-05-14 21:36:28 |
|
| [14] lorantfy | 2015-05-14 21:36:28 |
 Jó kis IQ teszt saját magadnak: Nézd meg a film elejét és próbálj rájönni, hogyan kódolja az időt ez az óra! Aztán persze mondhatod mindenkinek, hogy te 10 másodperc alatt rájöttél.
|
|
|
| [12] jonas | 2015-05-08 00:06:57 |
 Ő izé.
A kiegészítő feladat a következő. Tekintsünk most egy általánosabb lineáris rekurzióval definiált sorozatot a következőképpen. Legyenek &tex;\displaystyle p, q &xet; egész számok, &tex;\displaystyle a_0 = 0 &xet;, &tex;\displaystyle a_1 = 1 &xet;, és &tex;\displaystyle a_{n+1} = pa_n + qa_{n-1} &xet;. Az előző bizonyítás láthatóan nem használja ki a &tex;\displaystyle p &xet; és &tex;\displaystyle q &xet; értékeit, ezért továbbra is igaz, hogy &tex;\displaystyle a_k | a_{nk} &xet;.
A Fibonacci-sorozat esetén ebből be lehet látni a 12. állítást, vagyis hogy &tex;\displaystyle {\rm gcd}(F_n, F_k) = F_{{\rm gcd}(n,k)} &xet;. Hol romlik el a bizonyítás, a kicsit általánosabb &tex;\displaystyle {\rm gcd}(a_n, a_k) = a_{{\rm gcd}(n,k)} &xet; állítást akarjuk bebizonyítani? Mutassunk explicit ellenpéldát is, amikor ez az állítás nem igaz! Az ellenpélda lehetőleg kicsi, fejben ellenőrizhető legyen.
|
| Előzmény: [9] w, 2015-05-07 16:49:17 |
|
| [11] emm | 2015-05-07 22:05:30 |
 Persze, de sokszor az explicit formula nélkül, ha nem ismersz rengeteg azonosságot fejből, vagy esetleg nem mondják meg a zárt képletet, sokkal nehezebb elindulni (néha meg pont az explicit formulával szívás) ld. 5.-7. kérdés :)
(5)-re a következő képletig jutottam, ha nem néztem be semmit:
&tex;\displaystyle
5\sum_{i=1}^{n}F_{i}F_{ki}=
\frac{L_{(k+1)(n+1)}-(-1)^{(k+1)}L_{n(k+1)}+L_{(k+1)}-2(-1)^{k+1}}{L_{k+1}-1-(-1)^{k+1}}-
&xet;
&tex;\displaystyle
-\frac{(-1)^{n+k-1}L_{n(k-1)}+(-1)^nL_{(k-1)(n+1)}-L_{k-1}-2(-1)^{k-1}}{1+(-1)^{k-1}+L_{k-1}}&xet;
Egy ilyen bonyolultságú képletet hogy lehet megsejteni? :)
|
| Előzmény: [7] w, 2015-05-06 17:03:59 |
|
|
| [9] w | 2015-05-07 16:49:17 |
 A kiegészítő feladatot véletlenül nem írtad le. :)
A bizonyításodban van egy zavaró elírás, amikor a második sort írod, ott csak &tex;\displaystyle F_{k+1}\equiv F_{k+1}F_1&xet;, a &tex;\displaystyle 0&xet; nem írható úgy középre.
|
| Előzmény: [8] jonas, 2015-05-07 11:41:45 |
|
| [8] jonas | 2015-05-07 11:41:45 |
 A 10. és 12. állításokkal már találkoztam korábban, és nekem nagyon tetszenek. Viszont akkor mondok egy kiegészítő feladatot.
Én másképpen mondom el a 10-es bizonyítását. Vegyük észre, hogy
&tex;\displaystyle
F_k \equiv 0 \equiv F_{k+1} F_0 \mod F_k
&xet;
&tex;\displaystyle
F_{k+1} \equiv 0 \equiv F_{k+1} F_1 \mod F_k
&xet;
Ebből indukcióval jön, hogy bármely természetes &tex;\displaystyle l&xet;-re
&tex;\displaystyle
F_{k+l} \equiv F_{k+1}F_{l} \mod F_k
&xet;
Ha ezt most &tex;\displaystyle n &xet;-szer alkalmazzuk egymás után, ahol &tex;\displaystyle n &xet; természetes szám, akkor kijön, hogy &tex;\displaystyle F_k\left.\right.|\left.\right.F_{nk} &xet;
|
| Előzmény: [5] w, 2015-05-05 21:32:26 |
|
| [7] w | 2015-05-06 17:03:59 |
 Tehát ezek alapján a &tex;\displaystyle (9)&xet; azonosság elég hasznos a Fibonacci-számok között. (Nem tagadom, hogy az explicit &tex;\displaystyle \alpha,\beta&xet;-s Binet-formula rendkívül hatékony, de ha a homokozóban szeretnénk játszani, a buldózer elveszi a boldogságot. Ez elég "nyárias"/"teaszünetes" matematika lesz, de majd vissza lehet kanyarodni a komolyabb eredményekre.)
Csináljunk olyat, hogy elindulunk két tetszőleges számból: &tex;\displaystyle a,b&xet;. Ezután minden következő szám az előző kettő összege. Így a sorozat tagjai:
| 0. |
&tex;\displaystyle 1a+0b&xet; |
| 1. |
&tex;\displaystyle 0a+1b&xet; |
| 2. |
&tex;\displaystyle 1a+1b&xet; |
| 3. |
&tex;\displaystyle 1a+2b&xet; |
| 4. |
&tex;\displaystyle 2a+3b&xet; |
| 5. |
&tex;\displaystyle 3a+5b&xet; |
| ... |
... |
| &tex;\displaystyle n.&xet; |
&tex;\displaystyle F_{n-1}a+F_nb&xet; |
|
(Ha esetleg valakit zavarna, ez &tex;\displaystyle n=0&xet;-ra is értelmes, mert a Fibonacci-számok gond nélkül értelmezhetők negatív indexekre, az &tex;\displaystyle F_n=F_{n+2}-F_{n+1}&xet; "visszafelé-rekurzió" alapján.)
A kis játékunkból leolvasható (mi legyen &tex;\displaystyle a,b&xet;?):
| &tex;\displaystyle F_{n+m}=F_{n-1}F_m+F_nF_{m+1},&xet; | (9) |
| &tex;\displaystyle L_{n+m}=F_{n-1}L_m+F_nL_{m+1}.&xet; | (9b) |
&tex;\displaystyle &xet;
&tex;\displaystyle &xet;
Sikerült elég girbegurba utakon felfedezni a következő egyszerű azonosságot:
| &tex;\displaystyle L_n=F_{n-1}+F_{n+1}.&xet; | (13) |
Ennek a bizonyítása: &tex;\displaystyle n=0&xet;-ra &tex;\displaystyle L_0=F_{-1}+F_1=1+1=2&xet;, &tex;\displaystyle n=1&xet;-re &tex;\displaystyle L_1=F_0+F_2=0+1=1&xet;, és innen triviális teljes indukció.
Amúgy ha már itt tartunk, bármely &tex;\displaystyle a_{n+2}=a_{n+1}+a_n&xet; képzési szabályú sorozat egyértelműen előállítható két ilyen képzési szabályú &tex;\displaystyle b_n&xet; és &tex;\displaystyle c_n&xet; sorozatból &tex;\displaystyle a_n=xb_n+yc_n&xet; alakban, ahol &tex;\displaystyle x,y&xet; valamilyen konstansok, és &tex;\displaystyle b_n/c_n&xet; nemkonstans. Ez akkor legyen &tex;\displaystyle (14)&xet;. Merthogy az &tex;\displaystyle a_0&xet; és &tex;\displaystyle a_1&xet; meghatározza &tex;\displaystyle x,y&xet;-t, és innen indukció.
&tex;\displaystyle &xet;
&tex;\displaystyle &xet;
Új, indukciós bizonyítást adunk &tex;\displaystyle (3)&xet;-ra, vagyis arra, hogy &tex;\displaystyle F_{2n}=F_nL_n&xet;. Trivi az &tex;\displaystyle n=0&xet; eset. Majd írjuk fel &tex;\displaystyle (13)&xet;-at és &tex;\displaystyle (9b)&xet;-t speciális alakban:
&tex;\displaystyle F_{2n-2}+F_{2n}=L_{2n-1}=F_{n-1}L_{n-1}+F_nL_n.&xet;
Tegyük fel, hogy valamely &tex;\displaystyle n\ge 1&xet;-nél &tex;\displaystyle F_{2n-2}=F_{n-1}L_{n-1}&xet;, ekkor ebből rögtön &tex;\displaystyle F_{2n}=F_nL_n&xet;.
|
|
| [6] w | 2015-05-05 21:42:29 |
 Alternatív bizonyítások:
&tex;\displaystyle (F_{n+2}F_{n+1})^2-(F_nF_{n+1})^2=F_{2n+1}(F_{2n+2}-F_{2n})=F_{n+1}^2F_{2n+2}&xet;
következik abból, hogy (9) és a képzési szabály szerint
&tex;\displaystyle F_{2n+2}=F_nF_{n+1}+F_{n+1}F_{n+2}=F_{n+1}(F_{n+2}+F_n)=(F_{n+2}-F_n)(F_{n+2}+F_n)=F_{n+2}^2-F_n^2,&xet;
továbbá
&tex;\displaystyle F_{n+1}F_{n+2}F_{2n+3}-F_nF_{n+1}F_{2n+1}=F_{n+1}F_{3n+3}&xet;
pedig abból, hogy (9) és a képzési szabály szerint
&tex;\displaystyle F_{3n+3}=F_{n+1}F_{2n+1}+F_{n+2}F_{2n+2}=(F_{n+2}-F_n)F_{2n+1}+F_{n+2}(F_{2n+3}-F_{2n+1})=F_{n+2}F_{2n+3}-F_nF_{2n+1}.&xet;
|
| Előzmény: [3] emm, 2015-05-04 01:09:05 |
|
| [5] w | 2015-05-05 21:32:26 |
 Az egész topikban akkor fixen tisztázzuk, hogy &tex;\displaystyle F_0=0&xet;, &tex;\displaystyle F_1=1&xet;, &tex;\displaystyle F_{n+2}=F_{n+1}+F_n&xet; (&tex;\displaystyle n\ge 0&xet;) lesz a Fibonacci-sorozat, és &tex;\displaystyle L_0=2&xet;, &tex;\displaystyle L_1=1&xet;, &tex;\displaystyle L_{n+2}=L_{n+1}+L_n&xet; a Lucas-sorozat. (Furcsa indexeléseket is találni különböző helyeken.)
Most a (4) állítással kapcsolatban írok. Ennek egyszerű, az explicit formulát nem kihasználó bizonyítása is létezik, sőt általánosabb is érvényes.
(9) állítás. Ha &tex;\displaystyle i>0&xet;, &tex;\displaystyle j\ge 0&xet;, akkor
&tex;\displaystyle F_{i+j}=F_{i-1}F_{j}+F_iF_{j+1}.&xet;
Biz.: Legyen &tex;\displaystyle n=i+j&xet;. Igazából ez olyan, mintha elkezdenénk bontogatni az &tex;\displaystyle F_n&xet; számot:
&tex;\displaystyle F_n=F_{n-1}+F_{n-2}=2F_{n-2}+F_{n-3}=3F_{n-3}+2F_{n-2}=\dots=F_{\ell+1}F_{n-\ell}+F_{\ell}F_{n-\ell-1}.&xet;
Ha &tex;\displaystyle \ell=i-1&xet;, éppen &tex;\displaystyle (9)&xet; adódik.
(10) állítás. Ez lesz a &tex;\displaystyle (4)&xet;-es, vagyis hogy &tex;\displaystyle F_k|F_{nk}&xet;.
Biz.: Használjunk &tex;\displaystyle n&xet; szerinti indukciót. Az &tex;\displaystyle n=1&xet; eset triviális: &tex;\displaystyle F_k|F_k&xet;. Tegyük fel, hogy valamely &tex;\displaystyle n&xet;-re igaz, és alkalmazzuk &tex;\displaystyle (9)&xet;-et:
&tex;\displaystyle F_{(n+1)k}=F_{k-1}F_{nk}+F_kF_{nk+1},&xet;
és itt &tex;\displaystyle F_k|F_{nk}&xet; esetén a jobb oldal &tex;\displaystyle F_k&xet;-val osztható, így &tex;\displaystyle F_k|F_{(n+1)k}&xet; adódik. Kész az indukció.
(11) állítás. A szomszédos Fibonacci-számok relatív prímek, &tex;\displaystyle (F_n,F_{n+1})=1&xet;.
Biz.: Indukció (euklideszi algoritmus).
(12) állítás. Bármely &tex;\displaystyle n,m&xet; pozitív egészekre &tex;\displaystyle (F_n,F_m)=F_{(n,m)}&xet;.
Biz.: Ugyanannyit ad az az állítás, hogy &tex;\displaystyle (n,m)=1&xet; esetén &tex;\displaystyle (F_{dn},F_{dm})=F_d&xet;. Ennek belátásához &tex;\displaystyle n+m&xet; szerinti teljes indukciót használunk. Ha &tex;\displaystyle n+m=2&xet;, akkor &tex;\displaystyle (F_d,F_d)=F_d&xet; trivialitás adódik. Mostantól azt ecseteljük, hogy egy &tex;\displaystyle n,m&xet; párra az állítás következik a kisebb &tex;\displaystyle n+m&xet;-ekre vonatkozó állításból.
Ha &tex;\displaystyle n=m&xet;, akkor &tex;\displaystyle (n,m)=1&xet; miatt &tex;\displaystyle n=m=1&xet;: ezt már néztük. Ezért &tex;\displaystyle n\neq m&xet;, mondjuk &tex;\displaystyle m>n&xet; és &tex;\displaystyle m-n=k>0&xet;. Felhasználjuk &tex;\displaystyle (9)&xet;-et:
&tex;\displaystyle (F_{dn},F_{dm})=(F_{dn},F_{d(n+k)})=(F_{dn},F_{dn-1}F_{dk}+F_{dn}F_{dk+1})=(F_{dn},F_{dn-1}F_{dk}),&xet;
ahol &tex;\displaystyle (11)&xet; miatt ez éppen &tex;\displaystyle (F_{dn},F_{dk})&xet; lesz. Így ha &tex;\displaystyle k,n&xet;-re igaz az állítás, akkor &tex;\displaystyle n,m&xet;-re is. De &tex;\displaystyle k+n<n+m&xet;, így megvagyunk.
|
|
| [4] emm | 2015-05-04 01:26:24 |
 Néhány ötlet, általánosítás ezek alapján &tex;\displaystyle n,k&xet; poz. egészek - "zárt" azért, mivel &tex;\displaystyle k&xet;-tól fog függeni a megoldás:
(4) Lássuk be, hogy &tex;\displaystyle F_k|F_{nk}&xet; (ezek után kifejezetten egyszerűnek gondolnám)
(5) Keressünk "zárt" képletet &tex;\displaystyle \sum_{i=1}^n F_iF_{ki}&xet;-re
(6) Keressünk "zárt" képletet &tex;\displaystyle \sum_{i=1}^n F_{ki}/F_{i}&xet;-re
(7) Keressünk "zárt" képletet &tex;\displaystyle \sum_{i=1}^n (F_{i})^2 F_{ki}&xet;-re
(8) Bizonyítsuk be, hogy a &tex;\displaystyle 144&xet; a legnagyobb négyzetszám az &tex;\displaystyle F_n&xet; sorozatban. Mi a legnagyobb köbszám? stb. (utolsó 2 az extrém nehéz és ötletes és hosszú kategóriába esik, előbbire bizonyításvázlatot láttam csak)
|
|
| [3] emm | 2015-05-04 01:09:05 |
 Legyen &tex;\displaystyle x^2-x-1=0&xet; két gyöke &tex;\displaystyle \alpha=\frac{1+\sqrt{5}}{2}&xet; és &tex;\displaystyle \beta=\frac{1-\sqrt{5}}{2}&xet;, ekkor &tex;\displaystyle L_n=\alpha^n+\beta^n&xet; és &tex;\displaystyle F_n=\frac{\alpha^n-\beta^n}{\sqrt{5}}&xet;. Mivel kielégítik az egyenletet, ezért a következő igaz:
&tex;\displaystyle \alpha^2=\alpha+1, \alpha+\frac{1}{\alpha}=\sqrt{5}\qquad \beta^2=\beta+1, \beta+\frac{1}{\beta}=-\sqrt{5}&xet;
Azt a gondolatmenetet követjük, hogy &tex;\displaystyle \sum_{i=1}^n f(i)=g(n)&xet; bizonyításához elegendő &tex;\displaystyle f(n+1)=g(n+1)-g(n)&xet; és &tex;\displaystyle f(1)=g(1)&xet; egyenlőségeket belátni, mert így &tex;\displaystyle i=1,...,n&xet;-re összeadva pont azt kapjuk, amit látni szeretnénk.
(1) &tex;\displaystyle n=1&xet;-re igaz: &tex;\displaystyle F_1^2F_2=1=(F_1F_2)^2&xet;. Elegendő megmutatni, hogy:
&tex;\displaystyle (F_{n+2}F_{n+1})^2-(F_{n}F_{n+1})^2=F_{n+1}^2(F_{n+2}^2-F_{n}^2)=F_{n+1}^2 F_{2n+2}&xet;
De felhasználva a sorozat képzési szabályát, majd az explicit képletben kiemelve &tex;\displaystyle \alpha^{n+1}&xet;-t:
&tex;\displaystyle F_{n+2}^2-F_{n}^2=(F_{n+2}-F_{n})(F_{n+2}+F_{n})=F_{n+1}(F_{n+2}+F_{n})=\frac{\alpha^n-\beta^n}{\sqrt{5}}\left(\frac{\alpha ^{n+2}-\beta ^{n+2}}{\sqrt{5}}+\frac{\alpha ^n-\beta ^n}{\sqrt{5}}\right)=&xet;
&tex;\displaystyle =\frac{\alpha^{n+1}-\beta^{n+1}}{5}\left(\alpha^{n+1}\left(\alpha+\alpha^{-1}\right)-\beta^{n+1}\left(\beta+\beta^{-1}\right)\right)=\frac{(\alpha^{n+1}-\beta^{n+1})(\alpha^{n+1}+\beta^{n+1})}{\sqrt{5}}=F_{2n+2}&xet;
(2) &tex;\displaystyle n=1&xet;-re igaz, ugyanis: &tex;\displaystyle F_1F_2F_3=2=F_1F_3&xet;. Elegendő tehát megmutatni, hogy:
&tex;\displaystyle F_{n+1}F_{n+2}F_{2n+3}-F_{n}F_{n+1}F_{2n+1}=F_{n+1}F_{3n+3}&xet;
&tex;\displaystyle F_{n+1}&xet; kiemelhető, egyébként:
&tex;\displaystyle F_{n+2}F_{2n+3}-F_{n}F_{2n+1}-F_{3n+3}=&xet;
&tex;\displaystyle =\frac{1}{5} \left(\alpha ^{n+2}-\beta ^{n+2}\right) \left(\alpha ^{2 n+3}-\beta ^{2 n+3}\right)-\frac{\alpha ^{3 n+3}-\beta ^{3 n+3}}{\sqrt{5}}-\frac{1}{5} \left(\alpha ^n-\beta ^n\right) \left(\alpha ^{2 n+1}-\beta ^{2 n+1}\right)=&xet;
&tex;\displaystyle =-\frac{1}{5} \alpha ^{n+2} \beta ^{2 n+3}-\frac{1}{5} \alpha ^{2 n+3} \beta ^{n+2}+\frac{1}{5} \alpha ^{2 n+1} \beta ^n-\frac{1}{5} \alpha ^{3 n+1}-\frac{\alpha ^{3 n+3}}{\sqrt{5}}+\frac{1}{5} \alpha ^{3 n+5}+\frac{1}{5} \alpha ^n \beta ^{2 n+1}-\frac{1}{5} \beta ^{3 n+1}+\frac{\beta ^{3 n+3}}{\sqrt{5}}+\frac{1}{5} \beta ^{3 n+5}= &xet;
Most beírjuk, hogy &tex;\displaystyle -\alpha^{-1}=\beta&xet;:
&tex;\displaystyle =-\frac{1}{5} \alpha ^{3 n+1}-\frac{\alpha ^{3 n+3}}{\sqrt{5}}+\frac{1}{5} \alpha ^{3 n+5}+\frac{1}{5} (-\alpha )^{-3 n-5}-\frac{1}{5} (-\alpha )^{-3 n-1}+\frac{(-\alpha )^{-3 (n+1)}}{\sqrt{5}}= &xet;
&tex;\displaystyle =\frac{\left(\alpha ^4-\sqrt{5} \alpha ^2-1\right) (-\alpha )^{-3 n} \left(\alpha ^{3 n+6} (-\alpha )^{3 n}+1\right)}{5 \alpha ^5}=0 &xet;
Mivel &tex;\displaystyle \alpha&xet; megoldása az &tex;\displaystyle x^4-\sqrt{5}x^2-1=0&xet; egyenletnek.
(3) Mivel:&tex;\displaystyle \frac{F_2}{F_1}=1=4-3&xet; teljesül, ezért elegendő megmutatni, hogy&tex;\displaystyle L_{n+3}-3-(L_{n+2}-3)=L_n=\frac{F_{2n}}{F_n}&xet;, de:
&tex;\displaystyle \frac{F_{2n}}{F_n}=\frac{(\alpha^n-\beta^n)(\alpha^n+\beta^n)}{\sqrt{5}}:\frac{(\alpha^n-\beta^n)}{\sqrt{5}}=\alpha^n+\beta^n=L_n&xet;
|
| Előzmény: [2] gyula60, 2015-05-03 21:54:48 |
|
| [2] gyula60 | 2015-05-03 21:54:48 |
 Csapjunk a lecsó közepébe! Első közelítésben három sejtésre gondoltam, aminek a a bizonyításával még nem találkoztam:
&tex;\displaystyle \sum_{i=1}^nF_i^2F_{2i}=(F_nF_{n+1})^2,&xet; &tex;\displaystyle (1)&xet;
&tex;\displaystyle \sum_{i=1}^nF_iF_{3i}=F_nF_{n+1}F_{2n+1},&xet; &tex;\displaystyle (2)&xet;
&tex;\displaystyle \sum_{i=1}^n\bigg(\frac{F_{2i}}{F_i}\bigg)=&xet; &tex;\displaystyle L_{n+2}-3,&xet; &tex;\displaystyle (3)&xet;
ahol &tex;\displaystyle F_i&xet; és &tex;\displaystyle L_i&xet; az i-edik Fibonacci és Lucas számot jelölik, és az állítások igaznak bizonyultak minden egész n<21 indexre.
|
| Előzmény: [1] gyula60, 2015-05-03 21:35:31 |
|
| [1] gyula60 | 2015-05-03 21:35:31 |
 Ebben a topikban olyan feladványokkal lehet találkozni, amelyek a Fibonacci és a Lucas számokkal kapcsolatosak. A neten több csak e témakörrel kapcsolatos oldallal lehet találkozni. Nekem eddig Ron Knott oldala tetszett a legjobban, őszintén ajánlom minden érdeklődőnek: http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibpi.html#piandfib Nem kell sokáig böngészni, hogy megtaláljuk az első felfedezésre váró képleteket. Bízom benne, hogy nagyon sok gyerek örömét fogja lelni e témakörben.
|
|
