|
|
|
| [174] Suhanc | 2004-08-15 07:24:05 |
 Kedves László!
Átnéztem a feladatomat, és találtam rá egy lehetséges megoldást az eredeti szöveggel...
A [173]-as hozzászólásodban a levezetéssel egyetértek, kivéve, hogy :
"Balról jobbra olvasva az 1 és 10 közötti római számokból hármat nem lehet összerakni úgy, hogy értelmes római szám keletkezzen."
De lehet...:)
Ami talán nincs kellően kihangsúlyozva, hogy a könyveknek a közepén vannak a számok...
|
| Előzmény: [173] lorantfy, 2004-08-15 00:37:02 |
|
| [173] lorantfy | 2004-08-15 00:37:02 |
 Szia ScarMan!
Ha a történelmi könyvek a III, IV, V a 7-es meg nincs a polcon, akkor a megmaradó arab számok: 1+2+6+8+9+10=36.
Hogy lehet a III, IV, V számokból balról jobbra olvasva a 36-os számot kihozni?
Azt hiszem kicsit javítani kell a feladat szövegén!
A számok összege 1-től 10-ig 55. Ebből elvesszük a 7-et, marad 48, ennek a fele 24.
Balról jobbra olvasva az 1 és 10 közötti római számokból hármat nem lehet összerakni úgy, hogy értelmes római szám keletkezzen.
A maximum két számból XIX lenne, akkor a VII-es lehetne a harmadik történelmi, de a megmaradó arabok összege 29.
Így egyetlen kiutat látok, hogy Suhanc elírta a feladat szövegét!
Szerintem a javított szöveg:
A történelmi témájú könyvek egymás mellett vannak, számaikat jobbról balra egybeolvasva pontosan annyit kapunk, mint a mellettük levő arab számok összege.
Ekkor van megoldás: V, IX, X. Egybeírva: VIXX. Jobbról balra olvasva 24.
Jól gondolom?
|
| Előzmény: [172] ScarMan, 2004-08-14 22:06:18 |
|
|
| [171] Suhanc | 2004-08-09 20:49:02 |
 Ezt a feladatot 2 éve "barkácsoltam", remélem, azért az ujjgyakorlat minősítést megérdemli...:) Eredetileg a logikába szerettem volna írni, de ide talán jobban illik:
50.Feladat
Robi rendbe rakja könyvespolcát. Könyveit sorba rakja, és a könyvek gerincének a közepén számokat ír rá 1-től 10-ig.. Három könyve történelmi témájú, ezért ezekre a számot római számmal írja, majd fogja a hetes számot viselő könyvet, és elmegy otthonról. Hazaérve rémülten látja, hogy az öccse összekeverte könyveit. A történelmi témájú könyvek egymás mellett vannak, számaikat balról jobbra egybeolvasva pontosan annyit kapunk, mint a mellettük levő arab számok összege. Milyen számok vannak a történelmi könyveken?
|
|
|
| [169] Kós Géza | 2004-06-07 18:18:24 |
 Létezik több olyan osztási algoritmus, ami akárhány rabló esetére általánosítható.
Az egyik ilyen, hogy előbb A és B egymés között kétfelé osztják a kincset. Utána mindketten a saját fél kupacukat három-háromfelé osztják. Végül C az A-tól és a B-től is elvesz egy-egy kis kupacot.
|
|
| [168] Kós Géza | 2004-06-07 18:11:23 |
 Szerintem a leírt algoritmussal az 1. és a 3. rabló tud ugyanúgy összebeszélni. A 3. rabló egyenlőtlenül osztja el a kupacokat, utána az 1. rabló a három legnagyobb kupacot választja és a 2. hoppon marad.
|
| Előzmény: [165] lorantfy, 2004-06-07 14:27:21 |
|
| [167] Hajba Károly | 2004-06-07 17:06:01 |
 Javaslat a 49. feladathoz:
Az A rabló három részre osztja a kincset, majd B rabló kettő neki szimpatikus kupacot elvesz, s ha akarja átrendezi. Ezután C rabló mindháromból választva elveheti a neki tetsző részt. Ha C az első kupacot választja, akkor A válaszhat a maradék kettőből, míg ha az átrendezett kupacokból választott, akkor A viszi az első kupacot, B viszi a másik átrendezett kupacot.
A és B nem tudnak összebeszélni, mivel C szabadon válaszhat a három közül. A és C nem tudnak összebeszélni, mivel B alakította ki az átrendezett kupacokat és neki ebből az egyik jár. B és C nem tudnak összebeszélni, mivel A egyenletes szétosztása esetén nem tudják őt megkárosítani.
HK
|
| Előzmény: [164] Suhanc, 2004-06-06 11:24:29 |
|
| [166] Sirpi | 2004-06-07 15:36:19 |
 Ötletes a 27 részre osztás, az én megoldásomban azonban elég 6 részre osztani: Az első rabló osszon 3 részre, és a másik kettő válasszon.
1) Ha különbözőt választanak, akkor minden oké, mert mindketten viszik, amit választottak, és a megmaradó harmad az osztóé.
2) Akkor viszont gond van, ha a 2. és a 3. rabló ugyanazt a részt akarja magának. Ekkor ezt felezzék meg maguk között, és a maradék kettőből megint válasszanak.
2A) Ha ugyanazt választják, akkor azt is felezik maguk közt, a 3. az osztóé.
2B) Ha pedig nem ugyanazt választják, akkor mindketten a második választottjukat megfelezik az első rablóval.
Így könnyen végiggondolható, hogy mindegyikük el tudja érni, hogy megkapja legalább a harmadát a kincsnek.
Sirpi
|
| Előzmény: [165] lorantfy, 2004-06-07 14:27:21 |
|
| [165] lorantfy | 2004-06-07 14:27:21 |
 Egy ötlet a 49. feladathoz: Az első rabló felosztja a zsákmányt A,B,C részekre, majd a 2.rabló mindhárom részt újabb 3 részre: A1,A2..C3. Ezután a harmadik rabló választhat egy A, egy B és egy C részt, majd hasonlóan az első és a megmaradt részeket kapja a második rabló.
Ha az első két rabló nem harmadol igazságosan, akkor a 3. kiveszi a nagyobb részeket és jobban jár.
Még azt kell meggondolni, összebeszélhet-e bármelyik két rabló, hogy a harmadiknak kevesebb jusson mint a harmadrész, ők pedig megfelezik a kettőjüknek jutú részt.
Azt hiszem, gond van mert ha pl.a 2. és 3. rabló összebeszélnek, az első harmadol, a második pedig minden harmadot 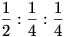 arányban oszt fel, a harmadik kiveszi a feles darabokat, a másik kettőnek maradnak a negyedek. Majd a 2. választ hasonlóan és 3. rabló elsztja egymásközt a szerzeményt. arányban oszt fel, a harmadik kiveszi a feles darabokat, a másik kettőnek maradnak a negyedek. Majd a 2. választ hasonlóan és 3. rabló elsztja egymásközt a szerzeményt.
Erre viszont az a megoldás - azt hiszem - ,hogy a harmadiknak is osztani kell, méghozzá minden darabot újabb 3 részre. Azután az 1.rabló választhat 9 db-ot a 27 részből, majd a 2. választ hasonlóan és a 3-nak marad 9 rész.
|
| Előzmény: [164] Suhanc, 2004-06-06 11:24:29 |
|
| [164] Suhanc | 2004-06-06 11:24:29 |
 Kedves Fórumosok!
Ezzel a feladattal még év elején találkoztam, egy általános iskolás feladatsorban:
49.Feladat:Két rabló a zsákmány úgy osztja szét, hogy egyikük két részre választja, a másik pedig kiválasztja belőle azt, amelyiket kapni akarja. Ezzel azt érik el, hogy másik stratégiájától függetlenül, biztosan meg tudják szerezni a zsákmány felét. Írjunk ilyen tulajdonsággal rendelkező algoritmust három rabló esetére!
|
|
| [163] lorantfy | 2004-05-27 15:27:02 |
 48. feladat: Hárman kártyáznak. A játék előtt pénzük aránya a:(a+1):(a+2), a játék után ugyanolyan sorrendben (a+1):(a+2):(a+3), s a kártyázás során csak egymástól nyerhettek. Egyikük 12 tallért nyert. Mennyi lehet az a egész szám értéke és hány tallérral ül le egy-egy játékos játszani, ha összesen kevesebb mint 2000 tallérjuk volt?
(Matematika próbaérettségi emelt szint 3. feladata alapján)
|
|
|
|
| [160] Hajba Károly | 2004-05-11 00:29:46 |
 Megoldás László nem is annyira ujjgyakorlat 32. feladatára:
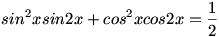
Három ismert trigonometriai egyenlőséget behelyettesítve:
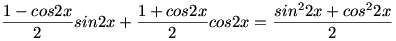
Majd szépen rendezve:
sin2x-sin2xcos2x+cos2x+cos22x=sin22x+cos22x
(sin2x+cos2x)-sin2x(sin2x+cos2x)=0
(sin2x+cos2x)(1-sin2x)=0
 1=67,5°;... 1=67,5°;... 2=157,5°;... 2=157,5°;... 3=45° 3=45°
|
| Előzmény: [109] lorantfy, 2004-02-10 08:18:20 |
|
| [159] BohnerGéza | 2004-05-09 11:13:36 |
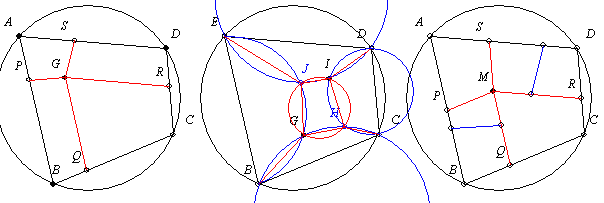
 A 42. feladathoz: (Mutassuk meg, hogy minden húrnégyszög felbontható n>=4 db húrnégyszögre.) A feladat régóta „áll”, ezért az „ujjgyakorlat” részét megírom, lerajzolom. Nem nehéz belátni, ha fel tudjuk bontani a 4-re, 5-re és 6-ra, akkor n>=4 tetszőleges db-ra is.
Az ábrán látható négyszögekről – leírom, hogy kaptam azokat – „ujjgyakorlat” megmutatni, hogy húrnégyszögek. Ami nehezebb, meg kell mutatni, hogy létezik megfelelő G, G és I, illetve M pont.
A nem triviális esetekben van hegyesszöge az ABCD húrnégyszögnek. Jelöljük egy ilyen csúcsát az A-val. ( Ekkor azt hiszem mindig léteznek az alább leírt felbontások esetén a megfelelő pontok. )
A négy részre bontást – ábra első része – úgy kapjuk, hogy megfelelő G-t választunk, majd legyen GR || AD, GQ || AB, valamint PBQB és GRDS húrtrapéz.
Az öt részre bontást – ábra középső része – úgy kapjuk, hogy a G és I pontokat felvesszük megfelelő helyre úgy, hogy a rajtuk és a megfelelő csúcsokon átmenő körök messék egymást még a H illetve J pontban.
Az hat részre bontást – ábra utolsó része – úgy kapjuk, hogy megfelelő M esetén a PBQM és MRDS „elég hosszú” paralelogrammák legyenek, majd azokat két-két húrtrapézra bontjuk.
|
 |
| Előzmény: [135] Csimby, 2004-04-11 22:16:40 |
|
| [158] Hajba Károly | 2004-05-07 12:27:10 |
 Kedves Péter!
Nem nehéz belátni a 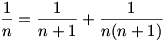 egyenlőséget, s ebből következik, hogy k=2 feltétel is elég. A jobb oldalt tovább lehet bontani és így akármeddig lehet bontogatni. egyenlőséget, s ebből következik, hogy k=2 feltétel is elég. A jobb oldalt tovább lehet bontani és így akármeddig lehet bontogatni.
Üdv: HK
|
| Előzmény: [156] nadorp, 2004-05-07 11:11:48 |
|
| [157] Kós Géza | 2004-05-07 12:09:28 |
 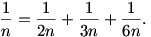
Az általánosabb feladat úgy szól, hogy minden pozitív racionális szám felírható véges sok különböző pozitív egész reciprokösszegeként. Ez ebben a formában nem ujjgyakorlat, de egy kis segítséggel az.
Vegyünk tehát egy pozitív racionális számot. A pozitív egészeket keressük ,,mohón'', azaz mindig a lehető legkisebbet válasszuk ki, ami még nem szerepelt, és a reciprokösszeg nem nő túl nagyra. Például, ha az 1,36 számot szeretnénk felírni, akkor a kiválasztott számok: 1, 3, 38, 2850.
47b feladat: Igazoljuk, hogy a mohó algoritmus mindig eredményre vezet.
|
| Előzmény: [156] nadorp, 2004-05-07 11:11:48 |
|
| [156] nadorp | 2004-05-07 11:11:48 |
 A 47. feladat kapcsán jutott eszembe.
47.a feladat: Bizonyítsuk be, hogy minden 1 nél nagyobb n pozitív egész szám reciproka előállítható k darab (2 k k n2) különböző pozitív egész reciprokának összegeként. n2) különböző pozitív egész reciprokának összegeként.
|
| Előzmény: [146] Hajba Károly, 2004-05-04 12:33:58 |
|
|
|
| [152] lorantfy | 2004-05-05 19:29:18 |
 Kedves Géza és Fórumosok!
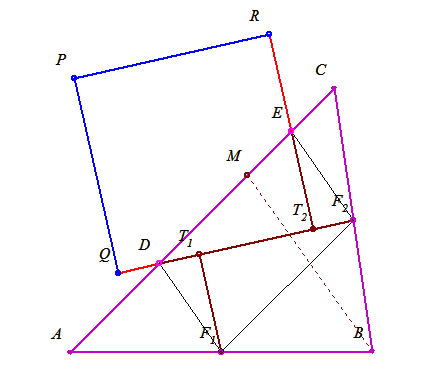
Valóban a B-ből induló magasságra nincs szükség, ez volt a félrevezetés, ui. egy "átlagos" hegyesszögű  -ben a talppontja elég közel esik ahhoz az M ponthoz amire négyzetet kapunk. -ben a talppontja elég közel esik ahhoz az M ponthoz amire négyzetet kapunk.
A DF1F2E paralelogramma DF2 átlója egyenlő a RPQT2 téglalap QT2 oldalával. Tehát, ha meg tudnánk szerkeszteni a leendő négyzet x oldalát, akkor F2 pontból kimetszhetnénk vele AC-ből a D pontot. Ezután A pont tükörképe D-re adja az M pontot.
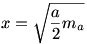 , tehát egyszerű mértani közép szerkesztéssel megkaphatjuk x-t az egyik oldal feléből és a hozzá tartozó magasságból. , tehát egyszerű mértani közép szerkesztéssel megkaphatjuk x-t az egyik oldal feléből és a hozzá tartozó magasságból.
|
 |
| Előzmény: [151] Kós Géza, 2004-05-05 13:55:04 |
|








 4=225° :o)
4=225° :o) 


 k
k MB.
MB. 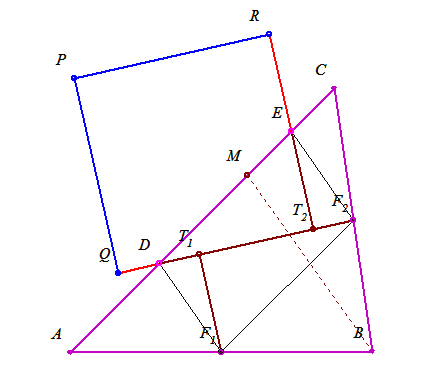
 -ben a talppontja elég közel esik ahhoz az M ponthoz amire négyzetet kapunk.
-ben a talppontja elég közel esik ahhoz az M ponthoz amire négyzetet kapunk. 