|
| [194] Lóczi Lajos | 2004-11-09 02:56:16 |
 Ha "csak úgy bele a közepibe", akkor
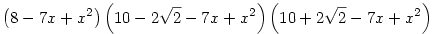 . .
Gyártottam még néhány feladatot erre a kaptafára, ezek kivétel nélkül másodfokúak szorzatára bonthatók:
(x-1)(x-2)(x-3)(x-4)(x-5)(x-6)+n=0, ahol n {...,-189,-96,-35,-5,9,15,16,21,64,135,...}. {...,-189,-96,-35,-5,9,15,16,21,64,135,...}.
Persze a tényezők számának és az 1,2,3,4,5,6 számoknak semmi szerepük sincs, pl. (x+1)(x-2)(x+5)(x+4)(x+2)+160=0 egy másodfokú és egy harmadfokú szorzatára bomlik... stb. stb. stb.
|
| Előzmény: [193] Gubbubu, 2004-11-08 19:37:04 |
|
| [193] Gubbubu | 2004-11-08 19:37:04 |
 58. feladat (ezt én Mosóczi András egyetemi hallgatótól ismerem)
Oldjuk meg az alábbi egyenletet:
(x-1)(x-2)(x-3)(x-4)(x-5)(x-6)+16=0
Nem kell megijedni ettől a jó kis hatodfokú egyenlettől. Ügyesen kell szorozgatni és alakítgatni, nem csak úgy bele a közepibe... :-))
|
|
| [192] lorantfy | 2004-11-07 20:00:53 |
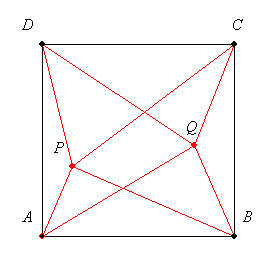
 57.feladat: Egy négyzet belsejében úgy vettünk fel két pontot, hogy az ezeket a négyzet négy csúcsával összekötő szakaszok a négyzetet kilenc, közös belső pont nélküli sokszögre darabolják.
Lehet-e a kilenc sokszög területe ugyanakkora?
(Varga Tamás verseny 1998.)
|
|
| [191] Gubbubu | 2004-10-08 09:48:03 |
 56. feladat: Igazoljuk, hogy tetszőleges háromszögben a szokásos jelölésekkel
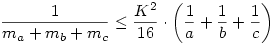
!
Hálás lennék, ha valaki felvilágosítana, mennyire "jó" ez a becslés, van-e jobb esetleg.
|
|
| [190] Suhanc | 2004-09-22 20:12:54 |
 Ja, ez lemaradt: a;b;c 0 0
|
|
| [189] Suhanc | 2004-09-22 20:12:09 |
 Elmúlt szakkörön vettük, és egy általános tétel jött ki belőle:
55.Feladat:
Igazoljuk az alábbi egyenlőtlenséget:
a3b+b3c+c3a a2bc+ab2c+abc2 a2bc+ab2c+abc2
|
|
|
| [187] Hajba Károly | 2004-09-14 15:02:23 |
 54. feladat: Melyik a nagyobb szám, az 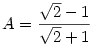 vagy a vagy a 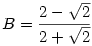 ? ?
HK
|
|
|
| [185] lorantfy | 2004-09-04 09:22:33 |
 53. feladat: Oldjuk meg a valós számok halmazán az egyenletet:
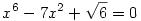
('96-os OKTV feladat. Mondjuk alakítsuk szorzattá!)
|
|
| [184] lorantfy | 2004-08-17 18:24:31 |
 52. feladat megoldása: x4-15x2-18x kifejezés minimumát kell meghatározni elemi módszerekkel.
Jó lenne átalakítani két teljes négyzet összegére, mégpedig úgy, hogy mindkettő ugyanazon x értéknél adjon nullát. A konstans nem számít, majd a végén levonjuk!
x4-15x2-18x=(x2-a2)2+b(x-a)2+c
Elvégezve a műveleteket és az azonos kitevőjű tagok együtthatóit összehasonlítva a köv. egyenletrendszert kapjuk:
2a2-b=15
ab=9
c=-a4-ba2
Az első kettőből 2a3-15a-9=0, látszik, hogy a=3 gyöke, így szorzattá alakítjuk:
(a-3)(2a2+6a+3)=0, a másodfokú gyökei 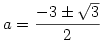 ez mindkettő negatív, 3-nál kisebb absz. értékű és b értéke is negatív. ez mindkettő negatív, 3-nál kisebb absz. értékű és b értéke is negatív.
Emiatt a c=-a4-ba2 értéke a=3-nál a legkisebb: b=3 és c=-108.
Tehát a konkrét átalakítás:
x4-15x2-18x=(x2-9)2+3(x-3)2-108
A kifejezés minimuma x=3-nál -108.
|
| Előzmény: [181] Suhanc, 2004-08-15 12:51:21 |
|
| [183] ScarMan | 2004-08-16 20:14:31 |
 Kedves László!
Mostmár látom, hogy félreértettem a feladatot. Azt hittem, hogy csak azokat a római számokat kell egybeolvasni, amik egymás mellett vannak... hát igen, így már teljesen más a feladat. Bocs az értetlenkedésemért!
|
| Előzmény: [173] lorantfy, 2004-08-15 00:37:02 |
|
| [182] Hajba Károly | 2004-08-15 14:09:48 |
 Kedves Suhanc!
Gratula, egyébként szerintem nincs más megoldás. Ezzel a feladattal még nem mentem a Szabadalmi Hivatalba, így teljes nyugalommal feladhatod. :o)
Hasonló feladatot - arab számokkal - felraktam az "Érdekes matekfeladatok" topikba is [325](74.), ott csak az egyik megoldást találta meg SchZol. Azzal a feladattal már nagyon régen találkoztam először, a római számos változatát most kreáltam, persze ez nem jeleti azt, hogy feltaláltam a spanyolviaszt.
HK
|
| Előzmény: [180] Suhanc, 2004-08-15 12:40:34 |
|
| [181] Suhanc | 2004-08-15 12:51:21 |
 Kedves Mindenki!
Ezzel a feladattal tegnapelőtt találkoztam... egy régi Arany Dani példa... lehet, hogy elsőre kissé favágónak tűnik:
52.FeladatHatározzuk meg az x4-15x2-18x kifejezés legkisebb értékét, ha x valós szám!
|
|
|
| [179] Hajba Károly | 2004-08-15 12:00:03 |

| Ebben a táblázatban |
| ... db I számjegy |
| ... db V számjegy |
| ... db X számjegy |
| ... db L számjegy |
| ... db C számjegy |
| ... db D számjegy |
| ... db M számjegy |
| található |
|
Hamár a római számoknál tartunk íme az 51. feladat. Természetesen római számjegyekkel kell kitölteni. :o)
HK
|
|
|
|
|
|
| [174] Suhanc | 2004-08-15 07:24:05 |
 Kedves László!
Átnéztem a feladatomat, és találtam rá egy lehetséges megoldást az eredeti szöveggel...
A [173]-as hozzászólásodban a levezetéssel egyetértek, kivéve, hogy :
"Balról jobbra olvasva az 1 és 10 közötti római számokból hármat nem lehet összerakni úgy, hogy értelmes római szám keletkezzen."
De lehet...:)
Ami talán nincs kellően kihangsúlyozva, hogy a könyveknek a közepén vannak a számok...
|
| Előzmény: [173] lorantfy, 2004-08-15 00:37:02 |
|
| [173] lorantfy | 2004-08-15 00:37:02 |
 Szia ScarMan!
Ha a történelmi könyvek a III, IV, V a 7-es meg nincs a polcon, akkor a megmaradó arab számok: 1+2+6+8+9+10=36.
Hogy lehet a III, IV, V számokból balról jobbra olvasva a 36-os számot kihozni?
Azt hiszem kicsit javítani kell a feladat szövegén!
A számok összege 1-től 10-ig 55. Ebből elvesszük a 7-et, marad 48, ennek a fele 24.
Balról jobbra olvasva az 1 és 10 közötti római számokból hármat nem lehet összerakni úgy, hogy értelmes római szám keletkezzen.
A maximum két számból XIX lenne, akkor a VII-es lehetne a harmadik történelmi, de a megmaradó arabok összege 29.
Így egyetlen kiutat látok, hogy Suhanc elírta a feladat szövegét!
Szerintem a javított szöveg:
A történelmi témájú könyvek egymás mellett vannak, számaikat jobbról balra egybeolvasva pontosan annyit kapunk, mint a mellettük levő arab számok összege.
Ekkor van megoldás: V, IX, X. Egybeírva: VIXX. Jobbról balra olvasva 24.
Jól gondolom?
|
| Előzmény: [172] ScarMan, 2004-08-14 22:06:18 |
|
|
| [171] Suhanc | 2004-08-09 20:49:02 |
 Ezt a feladatot 2 éve "barkácsoltam", remélem, azért az ujjgyakorlat minősítést megérdemli...:) Eredetileg a logikába szerettem volna írni, de ide talán jobban illik:
50.Feladat
Robi rendbe rakja könyvespolcát. Könyveit sorba rakja, és a könyvek gerincének a közepén számokat ír rá 1-től 10-ig.. Három könyve történelmi témájú, ezért ezekre a számot római számmal írja, majd fogja a hetes számot viselő könyvet, és elmegy otthonról. Hazaérve rémülten látja, hogy az öccse összekeverte könyveit. A történelmi témájú könyvek egymás mellett vannak, számaikat balról jobbra egybeolvasva pontosan annyit kapunk, mint a mellettük levő arab számok összege. Milyen számok vannak a történelmi könyveken?
|
|




 {...,-189,-96,-35,-5,9,15,16,21,64,135,...}.
{...,-189,-96,-35,-5,9,15,16,21,64,135,...}. 

 0
0 

