|
|
| [393] Edgar | 2005-10-30 19:32:45 |
 Nem tudom, szerepelt-e ez már... ha igen, elnézést :-)
Igazi gonosz kis ujjgyakorlat... Oldd meg a természetes számok körében:
x5-y2=4
|
|
| [392] Edgar | 2005-10-30 19:21:55 |
 így van :-) okosabb vagy, mint a nagykemény Maple szoftver... azaz ezer matematikusnál okosabb :-P ("Command the Brillance of a thousand mathematicians") azt hittem, majd befejti nekem, de magad uram lett belőle...
|
| Előzmény: [390] ágica, 2005-10-30 14:53:11 |
|
| [391] lorantfy | 2005-10-30 18:41:50 |
 Igazad van!
A 32.tesztfeladathoz kiegészítő kérdés: Hányadik tizedesjegytől ismétlődik a Fibonacci sorozat tagjaiból az ott leírt módon készített végtelen összeg racionális értéke.
|
| Előzmény: [389] Lóczi Lajos, 2005-10-30 13:32:48 |
|
|
| [389] Lóczi Lajos | 2005-10-30 13:32:48 |
 Nem következik, hogy nincs igaza!
Egy racionális számban nemcsak az első pár tizedeshelyen levő "89" alkothatja az ismétlődő részt, ezért a hozzászólásodból a "szebb" szó törlendő :)
|
| Előzmény: [387] lorantfy, 2005-10-30 11:22:22 |
|
| [388] Suhanc | 2005-10-30 12:46:17 |
 Kedves László!
Egy lehetséges megoldás:
Végezzük el egyenletünkkel a következő átalakításokat (x<>-5)!
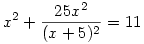
x2(x+5)2+25x2=11(x+5)2
x2(x+5)2+25x2+25(x+5)2=36(x+5)2
(x+5)2[x2+25]+25x2=36(x+5)2
(x+5)4-10x(x+5)2+25x2=36(x+5)2
[(x+5)2-5x]2=(6x+30)2
Ahonnan a2-b2=(a+b)(a-b) azonosságot felhasználva, és rendezve a tényezőket kapjuk, hogy:
(x2+11x+55)(x2-x-5)=0
Nyilván: x2+11x+55>0
Ezért csak x2-x-5=0 lehetséges, melyet
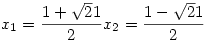 gyökök teljesítenek. gyökök teljesítenek.
|
| Előzmény: [382] lorantfy, 2005-10-29 11:54:41 |
|
| [387] lorantfy | 2005-10-30 11:22:22 |
 Nincs igaza, mert ha egy pontosabb géppel számolja rögtön kiderül, hogy a 89 számpár nem ismétlődik: 19,798989873223330683223642138936
Szebb indoklásra még várni kell!
Mindenesetre ha racionális szám lenne, akkor ez lenne az értéke: 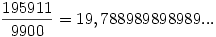
|
| Előzmény: [386] Lóczi Lajos, 2005-10-30 01:27:22 |
|
| [386] Lóczi Lajos | 2005-10-30 01:27:22 |
 77. feladat. Valaki számológéppel azt találta, hogy
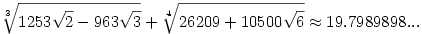
amiből azt sejti, hogy a fenti szám racionális. Igaza van-e?
|
|
|
|
|
| [382] lorantfy | 2005-10-29 11:54:41 |
 76. feladat: Oldjátok meg az egyenletet:
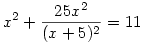
|
|
| [381] Róbert Gida | 2005-10-29 02:12:14 |
 Sokkal egyszerübben is meg lehet oldani ezeket, ha lnko(p,q)>1 most itt x59+y59=3, feltehető a szimmetria miatt, hogy x 0>y, továbbá x59=3+(-y)59 miatt, hogy x>-y, de akkor x59+y59 0>y, továbbá x59=3+(-y)59 miatt, hogy x>-y, de akkor x59+y59 x59-(x-1)59, de ez x-ben nyilván monoton nő, x=0;1-re nincs megoldás és x x59-(x-1)59, de ez x-ben nyilván monoton nő, x=0;1-re nincs megoldás és x 2-re x59+y59 2-re x59+y59 259-1, így nincs megoldás. 259-1, így nincs megoldás.
Ez általánosítható arra az esetre is, ha d=lnko(p,q)>1, használjuk, hogy a szomszédos d-edik hatványok különbsége monoton nő,mint az előbb és ha x ismert, akkor az egyenletből abs(y) is megkapható, így az egyenletnek véges sok megoldása lehet legfeljebb.
Az általános esetben feltehető, hogy p vagy q páratlan , különben lnko(p,q) 2 teljesül. Legyen például q páratlan, ekkor az egyenlet átírható ( az új y legyen a régi -y ).Az egyenlet 2 teljesül. Legyen például q páratlan, ekkor az egyenlet átírható ( az új y legyen a régi -y ).Az egyenlet
xp-yq=k
, ahol k nem nulla, akkor az egyenletnek minden k-ra véges sok megoldása van, ez S. S. Pillai sejtése, máig megoldatlan.
|
| Előzmény: [373] nadorp, 2005-10-27 09:55:27 |
|
| [380] Lóczi Lajos | 2005-10-28 23:19:38 |
 Igen, ezek a számok pár napja jó ismerőseim. :) (Az is érdekes kérdés még, hogy a minimális cáfolómodulushoz tartozó "alkalmas n-ek" halmaza micsoda, hányelemű, stb., de ez nyilván bonyolultabb kérdés lenne.)
|
| Előzmény: [379] Ali, 2005-10-28 14:46:34 |
|
| [379] Ali | 2005-10-28 14:46:34 |
 Mégegyszer átolvasva minmod(p,q) definícióját, és "alkalmas n"-hez keresve a minimális modulusokat ez jön ki:
minmod(3,3)=7
minmod(5,5)=11
minmod(7,7)=29
minmod(11,11)=23
minmod(13,13)=53
minmod(17,17)=103
minmod(19,19)=191
minmod(23,23)=47
minmod(29,29)=59
minmod(31,31)=311
minmod(37,37)=149
minmod(41,41)=83
minmod(43,43)=173
minmod(47,47)=283
Ebből valóban adódik a 2/a sejtés.
|
| Előzmény: [378] Ali, 2005-10-28 12:00:54 |
|
| [378] Ali | 2005-10-28 12:00:54 |
 Kicsit zavaros ez a minmod(p,q).
Pl.: x5+y5=7 egyenlet megoldhatságát az m=11 modulus cáfolja, míg x5+y5=13 -t m=25, az x5+y5=23 -t pedig m=31.
Akkor most melyik a minmod ?
|
| Előzmény: [377] Lóczi Lajos, 2005-10-27 22:56:47 |
|
| [377] Lóczi Lajos | 2005-10-27 22:56:47 |
 Tekintsük tehát az alábbi (*)
xp+yq=n
nemlineáris diofantoszi egyenletet, ahol p>2 és q>2 adott prímszámok, n valamely adott egész szám, és x, y a keresendő ismeretlen egészek. Ennek megoldhatatlanságát szeretnénk kimutatni bizonyos p, q kitevők mellett, alkalmas n jobboldalak esetén.
A (*) egyenlet nyilván megoldhatatlan, ha találunk egy alkalmas m 2 egész modulust, hogy (*) megoldhatatlan modulo m. 2 egész modulust, hogy (*) megoldhatatlan modulo m.
Gyakorlati szempontból az a fontos, ha minél kisebb ilyen m "cáfoló modulust" sikerül találnunk. Ezért pl. az alábbi számot szeretnénk meghatározni:
minmod(p,q) := min{m N| m N| m 2 és van olyan n 2 és van olyan n {1,2,...,m}, hogy minden x {1,2,...,m}, hogy minden x {1,2,...,m} és minden y {1,2,...,m} és minden y {1,2,...,m} esetén (*) NEM teljesül modulo m }. {1,2,...,m} esetén (*) NEM teljesül modulo m }.
1. sejtés. a.) Legyenek p q 2-nél nagyobb prímek, úgy, hogy 2pq+1 is prím. Ekkor minmod(p,q)=2pq+1. q 2-nél nagyobb prímek, úgy, hogy 2pq+1 is prím. Ekkor minmod(p,q)=2pq+1.
1. b.) Az összes "cáfoló modulus" minmod(p,q) pozitív egész többszöröse.
2. sejtés. a.) Ha p=q>2 prím, akkor minmod(p,p)=L.p+1, ahol L az a legkisebb pozitív páros szám, amire L.p+1 prím.
2. b.) Az 1. sejtés b.) része a p=q esetben nem igaz.
1. megjegyzés. Bonyolultabbnak tűnik a helyzet, ha a p vagy q számok összetettek is lehetnek.
2. megjegyzés. A 2.a.) sejtés analogonja nem tűnik igaznak a p q esetben: p=3 és q=19 esetén pl. minden m q esetben: p=3 és q=19 esetén pl. minden m 699 esetén megoldható az eredeti (*) egyenlet, akármilyen egész szám is az n jobboldal. 699 esetén megoldható az eredeti (*) egyenlet, akármilyen egész szám is az n jobboldal.
|
|
| [376] Lóczi Lajos | 2005-10-27 21:57:19 |
 De igenis "ujjgyakorlatok", programozási ujjgyakorlatok és "keress szabályszerűségeket a gép outputjában"-ujjgyakorlatok :) -- amíg nincs bizonyítás, addig biztosan.
|
| Előzmény: [375] Csimby, 2005-10-27 20:59:34 |
|
| [375] Csimby | 2005-10-27 20:59:34 |
 Talán nyithatnátok egy új topic-ot a témának, mert már nem igazán ujjgyakorlatok :-)
Euler sejtés: Ha s 2 és x1,...,xs,z,n pozitív egészek és x1n+x2n+...+xsn=zn, akkor s 2 és x1,...,xs,z,n pozitív egészek és x1n+x2n+...+xsn=zn, akkor s  n. n.
Ha ez igaz lenne, akkor következne belőle a Fermat-sejtés vagy Wiles-tétel ;-) is, azonban 1966-ban L.J. Lander és T.R. Parkin amerikai matematikusok találtak egy ellenpéldát (n=5,s=4):
a5+b5+c5+d5=1445
Keressük meg a megfelelő a,b,c,d pozitív egészeket. Az n=4,s=3 esetre az előbb említett két úr és J.L. Selfridge már 1967-ben megmutatták, hogy a x14+x24+x34=z4 egyenletnek biztosan nincs olyan pozitív egész megoldása, ahol x1,x2,x3,z mindegyike kisebb, mint 220000. Az első ellenpéldát Noam Elkies adta és megegyezik a 74. feladattal ([341]. hozzászólás). A legkisebb ismert ellenpéldát (n=4,s=3 esetén) R.Frye adta, és a [345]-ös hozzászólásban szerepel.
|
|
|
|
| [372] Lóczi Lajos | 2005-10-26 23:28:22 |
 Elkezdett foglalkoztatni, hogy hogyan lehet olyan modulusokat keresni, amelyek azt mutatják, hogy egy
xp+yq=n
alakú diofantoszi egyenletnek nincs megoldása. Mivel egy egysoros programmal sikerült jelentősen automatizálni az egyenletek átvizsgálását, több sejtést is kialakítottam. Ezeket hamarosan beírom ide. Addig is, álljon itt két újabb egyenlet, amelyek bizonyos szempontból a "legrosszabbul" viselkednek (minimális fokszám mellett a legnehezebb cáfolni a megoldásuk létét):
Oldjuk meg az egész számok körében az
x31+y31=31
egyenletet. Ugyanez a kérdés vonatkozik az
x59+y59=3
egyenletre.
|
|
| [371] Lóczi Lajos | 2005-10-25 00:21:04 |
 Megtaláltam, amire utaltál:
413=403+173+23=333+323+63,
de a 41 eme tulajdonsága hogyan kapcsolódik (ha egyáltalán) az x4+y5=1728 egyenlethez? Hiszen ezt az egyenletet úgy csináltam, hogy olyan legyen, hogy csak viszonylag "nagy" modulussal lehessen cáfolni, de az 1728 helyett a jobb oldalon nyugodtan lehetne 6 is (mivel ez kongruens 1728-cal modulo 41). Az 1728-nak számomra tehát semmi köze a 41-hez, csak azért választottam, hogy hamis asszociációkat keltsek. A mondandódból viszont az tűnik ki, mintha az 1728-ból jutott volna valahogy eszedbe a 41, mint cáfoló modulus. Ez vajon véletlen, vagy van valami a háttérben?
|
| Előzmény: [368] Káli gúla, 2005-10-24 23:03:26 |
|








 0>y, továbbá x59=3+(-y)59 miatt, hogy x>-y, de akkor x59+y59
0>y, továbbá x59=3+(-y)59 miatt, hogy x>-y, de akkor x59+y59 N| m
N| m q 2-nél nagyobb prímek, úgy, hogy 2pq+1 is prím. Ekkor minmod(p,q)=2pq+1.
q 2-nél nagyobb prímek, úgy, hogy 2pq+1 is prím. Ekkor minmod(p,q)=2pq+1.  699 esetén megoldható az eredeti (*) egyenlet, akármilyen egész szám is az n jobboldal.
699 esetén megoldható az eredeti (*) egyenlet, akármilyen egész szám is az n jobboldal.