|
| [469] Lóczi Lajos | 2005-11-17 22:26:32 |
 Köszönöm az érdekes fejleményeket az ügyben (és hogy vetted a fáradságot bepötyögni a mátrixokat :)
(Én kb. 2000-ben foglalkoztam ezzel a kérdéssel (lám, azóta sokminden felkerült az internetre...) és emlékszem, többszáz CPU-órát használtam fel. A 40800 ezek szerint a 4x4-es maximum, én is azt sejtettem, most már beugrott a szám. Láttam, hogy a 7x7-es eset alsó becslésével Pfoertner több, mint 2 évet számolt :-) )
A legérdekesebb, hogy ezek szerint nem mindig akkor adódik a maximális determináns, ha a főátlóban vannak a legnagyobb elemek.
|
| Előzmény: [467] Róbert Gida, 2005-11-17 21:10:06 |
|
| [468] Róbert Gida | 2005-11-17 21:17:16 |
 93. feladat
Egy nxn-es komplex elemű mátrix determinánsának kifejtésénél azt a meglepő dolgot tapasztaltuk, hogy mind az n! tag valós része pozitív. Milyen n-re lehetséges ez?
|
|
| [467] Róbert Gida | 2005-11-17 21:10:06 |
 Legyen x(n) a maximális determináns az nxn-es mátrixok közt, melynek elemei pontosan az 1,2,..,n2 számok. Triviálisan x(1)=1 és x(2)=10 ( főátlóban 4 és 3 ). Megoldásom szerint x(3)=412 Ekkor Sloane adatbázisában az 1,10,412 sorozatra rákeresve egyetlen találatot ad, a miénket! Ez az A085000 sorozat: http://www.research.att.com/projects/OEIS?Anum=A085000 Még állítólag 3 tag ismert a sorozatból!
x(4)=40800, mátrixot nem ad meg hozzá.
x(5)=6839492 mátrixot is ad hozzá:

x(6)=1865999570 ehhez is ad mátrixot:

Alsó becslések ( Hugo Pfoertner ): x(7) 762140212575 és x(8) 762140212575 és x(8) 440857916120379, x(7)-re ez már jobb becslés, mint amit Sloane-nál találhatunk, ez a http://www.recmath.org-on található. Itt éppen a te problémád egy javasolt programozási versenyfeladat, hogy minnél jobb becslést találjunk x(n) sorozatra. Nagyon kevés nyílt programozási verseny van a weben, jó ha 2. Ezek közül az egyik a híres Al Zimmermann prog. verseny: évente van 3-4 feladat és nagyon nagy dolognak számít ezen nyerni. Jelenleg is tart egy verseny: cél az 1,2,3,...,n sugarú körök bepakolása egy minimális sugarú körbe, hogy a körök diszjunktak legyenek. Ez a feladat 5 440857916120379, x(7)-re ez már jobb becslés, mint amit Sloane-nál találhatunk, ez a http://www.recmath.org-on található. Itt éppen a te problémád egy javasolt programozási versenyfeladat, hogy minnél jobb becslést találjunk x(n) sorozatra. Nagyon kevés nyílt programozási verseny van a weben, jó ha 2. Ezek közül az egyik a híres Al Zimmermann prog. verseny: évente van 3-4 feladat és nagyon nagy dolognak számít ezen nyerni. Jelenleg is tart egy verseny: cél az 1,2,3,...,n sugarú körök bepakolása egy minimális sugarú körbe, hogy a körök diszjunktak legyenek. Ez a feladat 5 n n 50-re. 50-re.
|
| Előzmény: [464] Lóczi Lajos, 2005-11-17 19:10:22 |
|
| [466] Káli gúla | 2005-11-17 20:21:54 |
 Igazad van, bár csupa negatív tagnál felcserélhetnénk két sort, és akkor csupa pozitív tagot kapnánk.
Egy újj gyakorlat. 92. feladat. A két és háromdimenziós kockának van egy érdekes tulajdonsága: ha a csúcsokat valahogy két azonos elemszámú részre bontjuk (elfelezzük), akkor a két ponthalmaz egybevágó lesz. Megvan-e ez a tulajdonsága a négydimenziós kockának is?
|
| Előzmény: [462] Róbert Gida, 2005-11-17 18:24:53 |
|
| [465] Róbert Gida | 2005-11-17 19:15:26 |
 Megoldás a 90. feladatra:
Ha A egy nxn-es mátrix, melynek minden eleme +-1, akkor a mátrix determinánsa osztható 2n-1-gyel. Ez n=1-re trivi, indukcióval, ha n=k-ra igaz, akkor n=k+1-re is igaz. Induljunk a csupa 1 mátrixból, ennek sorai összefüggnek, így determinánsa nulla, egy-egy lépésben a mátrix egy elemét -1-re változtatva bármely mátrixot megkaphatunk. Egy lépésben a mátrix determinánsát kifejtve abban a sorban, ahol egy elemet megváltoztattunk: az eredeti determináns+-2*aldetermináns lesz az új determináns, de az aldetermináns az indukció miatt osztható 2k-2-vel, így a determináns 2k-1-gyel osztható marad. Ami kellett.
Ha n>1 akkor a 0 mindig lehet a determináns: legyen A csupa 1 mátrix. Elég pozitív determinánsokat előállítani, mivel a determináns előjelet vált, ha két oszlopát felcseréljük.
n=3-ra a determináns legfeljebb 6, mivel 6 darab kifejtési tag van. De a determináns osztható 4-gyel. Így csak -4,0,4 lehet, ezek közül mindegyik előáll, az előbbiek miatt elég 4-re előállítást mutatni: legyen
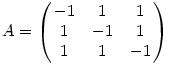
n=4-re 24 darab kifejtési tag van és a determináns osztható 8-cal, így csak -16,-8,0,8,16 lehet és mindegyik előáll, elég -8-ra és -16-ra példát mutatni: legyen
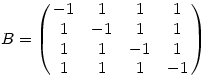
. Ekkor det(B)=-16 . Legyen
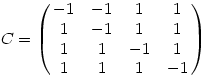
Ekkor det(C)=-8
|
|
| [464] Lóczi Lajos | 2005-11-17 19:10:22 |
 Régebben a 4x4-es analóg esetet is végigszámoltam, azzal a feltevéssel, hogy a főátlóban állnak a maximális elemek (tehát 16, 15, 14, 13). Aztán ha jól emlékszem valaki végigszámolta mindet és meghatároztuk a maximális elrendezést. Sajnos, nem látszott az általános minta. Milyen jó lenne látni pl. az 5x5-ös, stb. eseteket is... (tehát a mátrixot 1,2, ... , n2 számokkal feltöltve)
Aki ehhez hasonló problémákat akar keresgetni az interneten, az a Hadamard-féle maximális determinánsproblémára keressen pl. rá. Számos speciális alakú mátrix esetén ismert a maximum, de nem találtam eddig sehol eredményeket a fent feltett kérdésemre. Persze általánosabban is vizsgálható lenne a kérdés. Pl. egy ujjgyakorlat a következő:
Adott 4 valós szám. Mely elrendezés mellett lesz a belőlük képzett 2x2-es determináns abszolút értéke maximális?
|
| Előzmény: [463] Róbert Gida, 2005-11-17 18:41:47 |
|
| [463] Róbert Gida | 2005-11-17 18:41:47 |
 Megoldás a 89. feladatra:
A minimum egyszerű, legyen ugyanis:
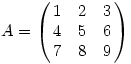
Ekkor A sorai lineárisan összefüggnek, így determinánsa nulla, így a minimum is nulla. A maximumra egy egyszerű program segítségével mind a 9! esetet végignézve ( persze lehetne kevesebbel is ), kapjuk, hogy a maximum 412 és ezt pl.
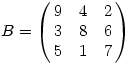
mátrixon vétetik fel. Egyébként nem véletlenül 412-öt is felveszi, mert ha -412 állna elő, akkor 2 oszlopát felcserélve a determináns ellentettjére vált.
|
|
| [462] Róbert Gida | 2005-11-17 18:24:53 |
 Valójában az indukció miatt az is kell, hogy pozítiv tag is van a kifejtési tagok közt. Amit persze ugyanúgy beláthatsz.
Megoldásom: n=3-ra szorozzuk össze a kifejtési tagokat, ekkor mivel a mátrix minden eleme két permutációban szerepel és a 6 féle permutáció közt 3 páros és 3 páratlan, ezért szorzatuk páratlan, így a kifejtési tagok szorzata 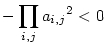 , de akkor a kifejtési tagok közt van pozitív és negatív is, ami kellett. , de akkor a kifejtési tagok közt van pozitív és negatív is, ami kellett.
|
| Előzmény: [456] Káli gúla, 2005-11-16 23:29:23 |
|
|
|
| [459] Lóczi Lajos | 2005-11-16 23:53:33 |
 90. feladat. Milyen értéket vehet fel egy 3x3-as mátrix determinánsa, ha minden mátrixelem (+1) vagy (-1)?
91. feladat. Mi a helyzet 4x4-es mátrix esetén?
|
|
| [458] Lóczi Lajos | 2005-11-16 23:45:56 |
 89. feladat. Mennyi lehet egy 3x3-as mátrix determinánsa abszolút értékének
a.) maximuma
b.) minimuma,
ha a mátrix elemei az 1, 2, 3,..., 9 számok (mindegyik pontosan egyszer)? Adjunk meg egy-egy extremális determinánsú elrendezést.
|
|
|
| [456] Káli gúla | 2005-11-16 23:29:23 |
 Ha mínuszból páratlan sok van, akkor valamelyik pozitív együtthatós hármasban is páratlan sok mínusz van. Ha mínuszból páros sok van, akkor valamelyik negatív együtthatós hármasban is páros sok van.
|
| Előzmény: [455] Róbert Gida, 2005-11-16 22:51:06 |
|
| [455] Róbert Gida | 2005-11-16 22:51:06 |
 Jó megoldás, először én is így csináltam n>3-ra, és n=3-ra végignéztem számítógéppel az 512 esetet, ez persze nem sok egy mai számítógéppel, kevesebb mint 1 másodperc alatt lefut. Aztán észrevettem egy számolás mentes bizonyítást n=3-ra! Mi lenne az?
|
| Előzmény: [454] Lóczi Lajos, 2005-11-16 22:36:09 |
|
| [454] Lóczi Lajos | 2005-11-16 22:36:09 |
 Mivel csak az előjel számít, feltehető, hogy minden elem a mátrixban +1 vagy -1.
n=2-re lehet minden kifejtési tag pozitív, pl. a bal alsó sarokban -1, a többi +1.
n=3-ra összesen 29-féle  1 mátrix van, ezeket szisztematikusan végigvizsgálva 32-féle különböző "kifejtési tag 6-os" adódik, ám mindegyik tartalmaz legalább egy (-1)-est, ÉS +1-est, tehát a kívánt tulajdonságú 3x3-as mátrix már nincs. 1 mátrix van, ezeket szisztematikusan végigvizsgálva 32-féle különböző "kifejtési tag 6-os" adódik, ám mindegyik tartalmaz legalább egy (-1)-est, ÉS +1-est, tehát a kívánt tulajdonságú 3x3-as mátrix már nincs.
És nincs n>3 esetén sem, mert -- pl. első sor szerint kifejtve -- a kifejtési tétel szerint ezt az nxn-es determinánst felírhatjuk n db (n-1)x(n-1)-es determináns előjeles összegeként, de akármelyik ilyen eggyel kisebb determináns kifejtésében lesz előjelváltás, tehát az eredeti nxn-es mátrix első sorát akárhogyan is választjuk meg  1-ek közül, az n db (n-1)! tagból álló kupac mindegyikében lesz előjelváltás. 1-ek közül, az n db (n-1)! tagból álló kupac mindegyikében lesz előjelváltás.
|
| Előzmény: [450] Róbert Gida, 2005-11-16 19:42:03 |
|
|
|
|
| [450] Róbert Gida | 2005-11-16 19:42:03 |
 87. feladat Egy nxn-es mátrix determinánsának a kifejtésénél azt a meglepő dolgot tapasztaltuk, hogy mind az n! darab tag pozítiv, milyen n-re lehetségez ez?
|
|
| [449] Lóczi Lajos | 2005-11-16 12:12:26 |
 86. feladat. Legyen n pozitív egész. Az 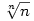 alakú számok között melyik a legnagyobb? alakú számok között melyik a legnagyobb?
|
|
|
| [447] Róbert Gida | 2005-11-16 00:58:20 |
 Azért nem kellenek komoly eszközök ehhez.
Tovább számolva: legyen n>1 ekkor
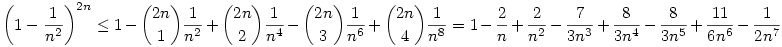
teljesül, hiszen könnyen bizonyíthatóan Leibnitz sor a binomiális sor részletösszegeinek sorozata, így most az első 5 tag egy felső becslést ad. Az egyenlőtlenség jobb oldalára pedig alsó becslést adva: 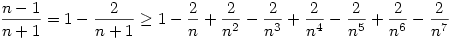 , ( ha nagy n-re akarnám belátni akkor elég lenne 4 tagot venni ) azaz elég belátni: , ( ha nagy n-re akarnám belátni akkor elég lenne 4 tagot venni ) azaz elég belátni:
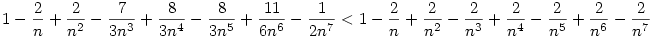
Rendezve és 6n7-tel szorozva kell: 2n4-4n3+4n2+n-9>0 kell, ami n>1-re triviálisan teljesül. Így beláttuk a feladatot.
Kétségtelen kicsit számolós, de ezt szerencsére a Maple végezte el.
|
| Előzmény: [446] Lóczi Lajos, 2005-11-15 21:53:28 |
|
| [446] Lóczi Lajos | 2005-11-15 21:53:28 |
 Azért szerintem ide kicsit komolyabb eszközök kellenek, mint az első pár tag. Egy standard módszer: (n-nek semmi jelentősége, hogy egész, ezért x-et írva)
vegyünk logaritmust és rendezgessünk egy kicsit, elegendő belátni, hogy x>1 esetén
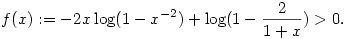
Könnyen látható, hogy f limesze 1-ben jobbról + , a végtelenben pedig 0. Továbbá , a végtelenben pedig 0. Továbbá
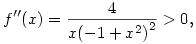
tehát f konvex. Ezek miatt f pozitív és az egyenlőtlenséget beláttuk.
|
| Előzmény: [444] Ali, 2005-11-15 14:40:53 |
|



 d
d 3 ( itt p egész ).
3 ( itt p egész ).



 [0,1] esetén lesz a [-1,1] intervallum komplementerén értelmezett
[0,1] esetén lesz a [-1,1] intervallum komplementerén értelmezett  1 mátrix van, ezeket szisztematikusan végigvizsgálva 32-féle különböző "kifejtési tag 6-os" adódik, ám mindegyik tartalmaz legalább egy (-1)-est, ÉS +1-est, tehát a kívánt tulajdonságú 3x3-as mátrix már nincs.
1 mátrix van, ezeket szisztematikusan végigvizsgálva 32-féle különböző "kifejtési tag 6-os" adódik, ám mindegyik tartalmaz legalább egy (-1)-est, ÉS +1-est, tehát a kívánt tulajdonságú 3x3-as mátrix már nincs.  , a végtelenben pedig 0. Továbbá
, a végtelenben pedig 0. Továbbá