|
|
| [650] bily71 | 2010-09-01 21:36:23 |
 Legyen a=b+c !
Ekkor:
5a=5b+5c
4b+4c=4a
Adjuk össze a két egyenletet!
5a+4b+4c=5b+5c+4a
Mindkét oldalból vonjunk ki 9a-t!
4b+4c-4a=5b+5c-5a
Ebből:
4(b+c-a)=5(b+c-a)
Vagyis 4=5. Hol a hiba?
|
|
|
| [648] jenei.attila | 2010-08-31 16:00:59 |
 Ne haragudj Bily, de a kérdést nem átfogalmaztad, hanem egyszerűen mást kérdezel. A négyzetmentes számokra igaz, hogy nem hatványszámok, de fordídva nem. A kezdőtagok nevezőiben pedig as szerepel, akármi is az a. Tehát az eredeti kérdésedben, ahol azt mondtad hogy az a négyzetmentes, nem fog szerepelni a 12s, mivel a 12 nem négyzetmentes. Ha most azt mondod, hogy az a mégis inkább legyen nem hatványszám, akkor szerepelni fog benne, mivel a 12 valóban nem hatványszám. Előbb döntsd el hogy mit kérdezel, és ne tegyél úgy mintha én lennék értetlen hülye! Legalább annyit írhattál volna, hogy bocsi, rosszul tettem fel a kérdést. Még hogy átfogalmaztad... Most felbosszantottál.
|
| Előzmény: [646] bily71, 2010-08-31 14:23:52 |
|
| [647] SAMBUCA | 2010-08-31 15:24:20 |
 Egyszerűen megválaszolható, ujjgyakorlat :) két dolgot kell ellenőrízni:
a, minden 1/ns szerepel a jobboldalon
b, egyik sem szerepel kétszer.
Sambuca
|
| Előzmény: [646] bily71, 2010-08-31 14:23:52 |
|
| [646] bily71 | 2010-08-31 14:23:52 |
 Szerintem meg a kezdőtagok nevezőiben az a számok azok a pozitiv egészek, amelyek nem állnak elő a=br alakban, ahol b és r pozitiv egészek és r>1, azaz bármely 1-nél nagyobb r esetén a r-edik gyöke nem egész szám.
Az 1/12s úgy lesz kezdőtag, hogy nem szerepel egyik előző sorban sem, vagyis igy:
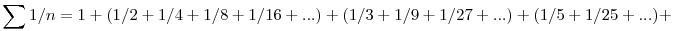
+(1/6+1/36+...)+(1/7+1/49+...)+(1/10+1/100+...)+(1/11+1/121+...)+(1/12+1/144+...)+...
Tehát a kérdésem átfogalmazva:
Igaz-e, hogy
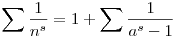
ahol a befutja a nem hatványszámokat, n pedig a pozitiv egészeket?
|
| Előzmény: [645] jenei.attila, 2010-08-31 08:53:06 |
|
| [645] jenei.attila | 2010-08-31 08:53:06 |
 Sajnos nem értem mire gondolsz: "csakhogy a kezdőtagok nevezőjében lévő a-k, mint ahogy az ellenpéldád is mutatja (az 1/12s is kezdőtag), nem azonosak a négyzetmentes számokkal"
Szerintem a kezdőtagok nevezői éppen a négyzetmentes számok. Továbbra sem találom az 1/12s-ent. Ez szerinted hogyan lesz kezdőtag? A következő hozzászólásodban az r mit jelent? Mi az, hogy az r-edik gyök nem egész szám? Létezik ilyen r, vagy minden r-re? Légyszíves próbáld ezt világosabban kifejteni. Köszi.
|
| Előzmény: [643] bily71, 2010-08-30 22:33:35 |
|
|
| [643] bily71 | 2010-08-30 22:33:35 |
 s=1 esetén:
1/1+1/2+1/3+...=1+(1/2+1/4+1/8...)+(1/3+1/9+1/27+...)+(1/5+1/25+1/125+)+...
s=2 esetén:
1/1+1/4+1/9+...=1+(1/4+1/16+1/64+...)+(1/9+1/81+1/729+...)+(1/25+1/625+1/15625+...)+...
...
A zárójelekben olyan mértani sorok vannak, melyek kezdőtagjai nem szerepeltek egyik elöző zárójelben sem és a kezdőtag egyenlő a kvócienssel, csakhogy a kezdőtagok nevezőjében lévő a-k, mint ahogy az ellenpéldád is mutatja (az 1/12s is kezdőtag), nem azonosak a négyzetmentes számokkal, ezen számok halmaza bővebb.
|
| Előzmény: [641] jenei.attila, 2010-08-30 12:23:13 |
|
|
|
|
|
|
| [637] bily71 | 2010-08-29 15:54:31 |
 Igaz-e, hogy
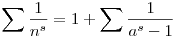
ahol s N, n végigfut a természetes számokon, a pedig az 1-nél nagyobb négyzetmentes számokon ? N, n végigfut a természetes számokon, a pedig az 1-nél nagyobb négyzetmentes számokon ?
|
|
|
| [635] BohnerGéza | 2010-08-23 21:03:07 |
 Ha a csomó a lyukhoz ér, megáll. Egy súly nem emeli föl a másikat, hisz egyenlők. Addig történhet mozgás, míg a harmadik súly rásegít, de ez véget ér, ha a csomó a lyukhoz ér.
Érdemes helyzeti energia szempontjából is vizsgálni a feladatot:
Akkor áll meg a súlyok mozgása (persze, ha csillapodás is van), ha az összes helyzeti energiájuk a legkisebb, azaz az asztal fölött a madzagok összhossza a legkisebb. Tehát azt a pontot keressük, melyre a tőle a csúcsokig tartó szakaszok összege minimális.
Ez az olyan háromszögeknél, melyek minden szöge kisebb 120 foknál, valóban az izogonális pont. Az olyan háromszögeknél, melynek van legalább 120 fokos szöge, ennek csúcsa.
|
| Előzmény: [633] SmallPotato, 2010-08-22 14:39:35 |
|
|
| [633] SmallPotato | 2010-08-22 14:39:35 |
 A jelzett esetben valóban nem állhat elő a három egyforma szög; ebből adódóan viszont ekkor a három egyenlő nagyságú erő nem tarthat egyensúlyt. Konkrétan az fog történni, hogy a 120 fokot elérő szögnél levő lyukba az ott lévő súly berántja a csomót és a rendszert csak valamelyik másik súly elakadása állítja meg.
Olyasmi helyzet ez, mint az utca két oldala között kifeszített tartókábel és az azon, (az egyszerűség kedvéért most középen) lógó lámpa. Ha a tartókábel túl feszes (azaz két ága az egyenesszöghöz közeli szöget zár be), a felfüggesztésben lényegesen nagyobb erők ébrednek, mint a lámpa súlya. Konkrétan ha a tartókábel ágai 120 foknál többet zárnak be, akkor a bennük ébredő erő a lámpa súlyánál nagyobb kell hogy legyen; vagy megfordítva: ha a feszítőerőnek nem szabad meghaladnia a lámpa súlyát, akkor a szög nem haladhatja meg a 120 fokot.
|
| Előzmény: [631] gubanc, 2010-08-22 12:03:56 |
|
| [632] bily71 | 2010-08-22 14:12:35 |
 1Ft=100f=10f*10f=1/10Ft*1/10Ft=1/100Ft=1f, vagyis 1 forint=1 fillér.
Hol a hiba?
|
|
| [631] gubanc | 2010-08-22 12:03:56 |
 Ezt a példát már én is hallottam, de diszkussziós választ még nem. A feladat tetszőleges háromszögről szól. Kós Géza a GEOMETRIA [268]-ban ezt írja: „Ha valamelyik szög éppen 120 fok vagy annál nagyobb, akkor nincs izogonális pont”. Ha ez igaz, hol lesz a csomó az ilyen háromszögeknél és mi a teljes indoklás?
|
| Előzmény: [630] Fernando, 2010-08-22 08:39:22 |
|
| [630] Fernando | 2010-08-22 08:39:22 |
 Szerintem ez az ún. izogonális pont, ahonnan a háromszög három oldala azonos szög alatt látszik = a csúcsokhoz vezető szakaszok hosszösszege minimális.
|
|
|
|







 N és r>1 esetén nem egész szám.
N és r>1 esetén nem egész szám.



