| [209] Lóczi Lajos | 2005-11-04 20:46:17 |
 Ezzel kapcsolatban a következők jutottak eszembe. A Fourier- és Laplace-transzformációkkal szoktunk az integráltranszformációk közül leggyakrabban találkozni. Ha a transzformálandó függvény a negatív számokon nem érdekes (pl. azonosan nulla), akkor jó a Laplace-transzformációt alkalmazni. Továbbá, ha a függvény a plusz végtelen felé haladva nem csökken elég gyorsan, akkor a Fourier-transzformációban szereplő integrál esetleg nem lesz konvergens. Ekkor is előnyös a Laplace-tr., amely tehát egyfajta súlyozott Fourier-tr.-ként fogható fel: a súlyfüggvény az exponenciális függv. Mivel ez gyorsan csökken, az integrált konvergenssé teheti, akár még exponenciálisan gyorsan növő f-ek esetén is. (Az a bizonyos s a súlyfüggvény kitevőjében a Laplace-transzformáció konvergenciafélsíkjának szélét határozza meg.)
A Laplace-tr. tipikus alkalmazásai közé tartozik bizonyos differenciálegyenletek megoldása. A diff. egyenletet transzformálva egy "algebrai" egyenletet kapunk. Ennek megoldását kell vissza-Laplace-transzformálni, hogy megkapjuk az eredeti diff. egyenlet megoldását. Nyilván ez utóbbi lépés a legnehezebb, ezen múlik a módszer sikere és alkalmazhatósága.
|
| Előzmény: [208] Wolf, 2005-11-04 11:43:09 |
|
| [208] Wolf | 2005-11-04 11:43:09 |
 Üdvözletem!!!
Elnézést, gondolhattam volna... Tehát arra vagyok kiváncsi, ha az időfv.-em w körfrekvencia szerint változik, akkor a fv. Laplace-transzformáltja a komplex számsíkon ábrázolható.Ennek a transzformálásnak mi a jelentősége, hogy kell elképzelni? Mivel a sin(wt) L.Tr.-ja valós részű, és a cos(wt) L.tr.-ja képzetes részű, akkor ezek kombinációival (pl.:Fourier-sor) egy jelleggörbét kapok a kompl.sz.-on? Ezen vektorok jellemzéséből utaltam az e(-st) tagra, melyett mindig fel kell használni... Mit befolyásol ez a tag a transzformálás során, mi az "s"? Sajnos nincs kellő átlátásom az adott témáról, elnézést ha éppenséggel "hülyeséget" írtam. Tudom kicsit már fizika, de nagy szükségem lenne a segítségére, köszönöm!!!
|
| Előzmény: [200] Lóczi Lajos, 2005-11-01 20:52:53 |
|
| [207] Lóczi Lajos | 2005-11-03 22:17:18 |
 A levezetés nekem sosem kellett, csak a formulákat használtam (többdimenziós esetben). Hallottam, hogy ezek a formulák szoros kapcsolatba hozhatók kombinatorikus fákkal és gráfokkal, tehát ilyen könyvekben is keresgélhetsz.
|
| Előzmény: [206] Tibi, 2005-11-03 08:31:26 |
|
| [206] Tibi | 2005-11-03 08:31:26 |
 Keressgettem és találtam is valamit a levezetésről, de én másképp oldottam meg: teljes indukcióval. Csinálta más is?
|
|
| [205] Tibi | 2005-11-03 08:12:56 |
 Az ok, hogy a formulák nyelvfüggetlenek, de engem a képlet bizonyítása érdekelne...magyarul.Nem tudod, merre találhatnám meg?Egyáltalán benne van ez valamilyen tankönyvben?
|
| Előzmény: [204] Lóczi Lajos, 2005-11-02 22:09:15 |
|
|
|
|
| [201] Tibi | 2005-11-02 21:03:20 |
 Sziasztok!
Lehet, hogy most butaságot fogok kérdezni, de tud valaki képletet az összetett függvények magasabbrendű deriváltjainak előállítására? Én egy könyvben sem találok ilyet. Köszönöm a választ!
|
|
|
| [199] Lóczi Lajos | 2005-11-01 20:50:38 |
 http://mathworld.wolfram.com/LaplaceTransform.html
igaz, hogy angol, de a képleteket lehet érteni. Néhány függvény Laplace-transzformáltja benne van. (Esetleg konkrétabb kérdést is megfogalmazhatsz itt, miután elolvastad és megpróbálunk válaszolni rá.)
|
| Előzmény: [198] Wolf, 2005-11-01 20:39:02 |
|
| [198] Wolf | 2005-11-01 20:39:02 |
 Üdvözletem!!!
Szeretném megkérdezni, hogy a Laplace-transzformáció tulajdonképpen miről szól és mit jelent az F(s)=integral[F(t)e(-st)1(t)dt] alakból az exponenciális tag, ahol 1(t) az egységugrás és 0-infinity intervallumban vizsgáljuk? Esetleg hol tudok ennek utánanézni(magyar leírás)?
U.i.: Bocs, hogy így adtam meg... Köszönöm
|
|
|
| [195] Lóczi Lajos | 2005-10-13 10:09:49 |
 Ha a számláló foka nagyobb, nem biztos, hogy a végtelenbe tart a tört, tarthat (- )-hez is, ha a nevező pl. negatív :) )-hez is, ha a nevező pl. negatív :)
Ha a számláló foka nagyobb, akkor is a nevező fokával célszerű egyszerűsíteni, így a nevező véges, NEMNULLA számhoz fok tartani, míg a számláló valamelyik végtelenbe. (Ha a számláló fokszámával egyszerűsítenél, akkor "túlegyszerűsítenél": a nevező nullához tartana, ami önmagában kényes, elkerülendő.)
|
| Előzmény: [194] madár2, 2005-10-13 08:57:23 |
|
| [194] madár2 | 2005-10-13 08:57:23 |
 Köszönöm szépen! A fő kérdés, az a precíz átalakításra vonatkozott, de megértettem. Még annyit kérdeznék, ha lehet, hogy ha a számláló foka nagyobb (akkor nyilván a végtelenbe tart), akkor az "x a számláló fokán"-nal kell egyszerűsíteni, igaz?
|
| Előzmény: [193] Lóczi Lajos, 2005-10-12 20:29:59 |
|
| [193] Lóczi Lajos | 2005-10-12 20:29:59 |
 Nézzünk akkor egy ilyet például:
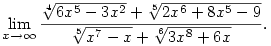
A lényeg, hogy lássuk minden gyök alatt mi a "domináns" nagyságrend, ha x "nagy".
A számláló nagyságrendje nyilván
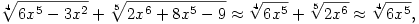
mert (x-kitevőit nézve) 5/4>6/5.
A nevező nagyságrendje
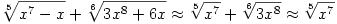
hiszen 7/5>8/6.
Azt kaptuk tehát, hogy az eredeti tört (nagy x-ek esetén)
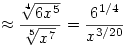
nagyságrendű. Ennek a limesze viszont a végtelenben nyilván 0.
E sejtés kialakítása után a precíz kivitelezés már könnyű: a törtet, szokás szerint, egyszerűsítjük a nevező "legnagyobb fokszámú tagjával", azaz a megfelelő x-nagyságrenddel. Jelen esetben tehát a törtet 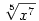 -nel kell egyszerűsíteni. Ekkor az egyszerűsített tört számlálója 0-hoz tart (hiszen 7/5>5/4 és 7/5>6/5), a nevező viszont egy véges, nemnulla számhoz (t.i. 1-hez) tart, az egész törtkifejezés tehát tényleg 0-hoz fog konvergálni. -nel kell egyszerűsíteni. Ekkor az egyszerűsített tört számlálója 0-hoz tart (hiszen 7/5>5/4 és 7/5>6/5), a nevező viszont egy véges, nemnulla számhoz (t.i. 1-hez) tart, az egész törtkifejezés tehát tényleg 0-hoz fog konvergálni.
|
| Előzmény: [191] madár2, 2005-10-12 15:07:27 |
|
|
| [191] madár2 | 2005-10-12 15:07:27 |
 az n az fix, mondjuk a számlálóban 4, a nevezőben 5. (de olyan feladat is van, ahol két különböző gyök összege van a számlálóban) a 4. gyök alatt a polinom foka 5, az 5. gyök alatt 6 a foka. (még nem megy a tex, most léptem be először, bocs)
|
|
|
| [189] madár2 | 2005-10-12 13:32:53 |
 Sziasztok! Valaki meg tudná nekem sürgősen mondani, hogy kell megcsinálni, a: végtelen/végtelen tipusú határérték feladatot, ha szerepel/nek banne n.gyökök is, és a gyök alatt álló polinom foka nagyobb, mint az n. (a gyökön) a módszer érdekelne, tudom, hogy nem középiskolás anyag, de fontos lenne. 8tanultam, és elfelejtődött) köszi
|
|
| [188] Lóczi Lajos | 2005-10-12 10:25:21 |
 Persze. Legyen a>1/2. A (konvergencia szempontjából) lényegtelen konstansokat elhagyva elég ezt nézni:
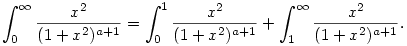
Az első integrandus nyilván korlátos, az integrál tehát véges. A másik integrandus viszont felülről becsülhető
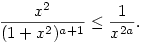
Itt 2a>1, és ismert, hogy ilyenkor 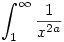 konvergens. konvergens.
|
| Előzmény: [187] rizsesz, 2005-10-11 22:07:36 |
|
| [187] rizsesz | 2005-10-11 22:07:36 |
 minden a>1/2-re konvergens?
|
|
| [186] Lóczi Lajos | 2005-10-11 20:31:32 |
 A végeredmény jónak tűnik, azonban az integrál csak a>1/2 esetén konvergens, különben divergens. (Ha a komplex szám is lehet, akkor a valós része legyen nagyobb 1/2-nél.)
|
| Előzmény: [185] nadorp, 2005-10-11 19:52:32 |
|
| [185] nadorp | 2005-10-11 19:52:32 |
 No comment, ilyen volt a példa, egyszerűbb megoldást nem látok. De lehet, hogy igazad van és legközelebb E-mailben válaszolok a kitűzőnek, ha a példa jóval meghaladja a középiskolai anyagot.
Üdv
|
| Előzmény: [184] hobbymatekos, 2005-10-11 17:02:17 |
|
|






 )-hez is, ha a nevező pl. negatív :)
)-hez is, ha a nevező pl. negatív :) 