| [410] Cckek | 2006-10-16 23:08:44 |
 Akkor egyszerűsítek:))Számítsuk ki 100! számjegyeinek a számát. Különben a becslés hibás hisz 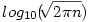 nem elhanyagolható:)) nem elhanyagolható:))
|
|
| [409] Sirpi | 2006-10-16 20:56:42 |
 A pontos válasz [log10n!]+1, amivel sokkal nem vagyunk előrébb, viszont igen jó közelítést könnyen lehet adni a Stirling-formula alapján (ez azt mondja ki, hogy 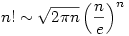 ). Eszerint n! számjegyeinek száma kb. n(log10n-log10e), vagyis nagyságrendileg nlog10n. ). Eszerint n! számjegyeinek száma kb. n(log10n-log10e), vagyis nagyságrendileg nlog10n.
|
| Előzmény: [408] Cckek, 2006-10-16 20:03:44 |
|
| [408] Cckek | 2006-10-16 20:03:44 |
 Nos jó. Akkor már kitűzhetem a következő kis feladatot: Adjunk képletet mely kiszámítja n! számjegyeinek a számát:))
|
|
|
| [406] Sirpi | 2006-10-16 18:47:27 |
 Egy szám 10-es alapú logaritmusa mondja meg, hogy hány jegyű, nevezetesen egy N szám jegyeinek száma [log10N]+1, hiszen 1 és 10 között a logaritmus egészrésze 0, a jegyek száma 1. Ugyanígy 10 és 100 közt az egészrész 1, a jegyek száma 2 stb. Most írj N helyére 2n-et, használd fel hogy log ab=blog a és kész. Bocs mindenkitől, ha túlragoztam volna csak nem tudom ennek melyik része lehetett bonyolult :-)
|
| Előzmény: [405] Cckek, 2006-10-16 18:36:10 |
|
|
|
| [403] Cckek | 2006-10-16 14:56:14 |
 A következő egyszerünek tűnő problémához kéne egy kis segítség: Határozzuk meg 2n számjegyeinek a számát. Persze ezt lehet általánosítani de már ebben a formában is nagyon nehéznek tűnik.
|
|
|
|
| [400] qkac | 2006-10-15 21:56:22 |
 Így van megadva a feladat:
Milyen számot(betűt) írjunk az x helyébe, hogy az alábbi egyenlőségláncolatok igazak legyenek? (A hatványalapok mindegyike 1-től különböző pozitív valós szám) a) a3=b4=(ab)x b) p2=q3=(pq)2x
|
| Előzmény: [399] Lóczi Lajos, 2006-10-15 21:50:30 |
|
|
|
|
| [396] qkac | 2006-10-15 20:09:55 |
 Valaki nem tudja levezetni ezt a két példát? a) a3=b4=(ab)x b) p2=q3=(pq)2x Milyen számot(betűt) írjunk az x helyébe, hogy az alábbi egyenlőségláncolatok igazak legyenek?
|
|
|
|
|
| [392] Sirpi | 2006-10-04 09:16:59 |
 a) igen b) nem
Amúgy szerintem ha 1,4-szeresnek adod meg a sebességet, azzal túl sokat árulsz el, úgy nem annyira feltűnő, hogy min múlik a dolog, ha azt mondod, hogy Jerry 5m/s sebességgel tud úszni, a macskák pedig 7m/s sebességgel tudnak futni.
Mondjuk ekkor vagy Jerry úszik rekordsebességgel, vagy a macskák vannak nagyon ellustulva :-) Én amúgy úgy ismertem, hogy négyzet alakú karám, középen egy bárány, a 4 sarokban farkasok, és körben kerítés, de a bárány át tud bújni alatta, viszont a farkasok nem. Tudom, semmit nem változtat, csak gondoltam leírom :-)
Megoldást pedig egyelőre nem szeretnék közzétenni, remélem nem baj.
|
| Előzmény: [391] rizsesz, 2006-10-03 23:43:58 |
|
| [391] rizsesz | 2006-10-03 23:43:58 |
 Kedves Sirpi, még egyszer köszönöm. Tudom, nem ez a típus, de hátha: :)
Négyzet alakú medencében úszkál Jerry. Megjelenik 4 Tom :) a medence 4 sarkánál, akik macskák, így nem mennek a vízbe. A macskák 1,4 szer olyan gyorsan haladnak kint, mint Jerry a vízben. El tudja-e érni Jerry úgy a partot, hogy abban a pillanatban, amikor kiért, ott ne legyen macska? A macskák persze rendkívül intelligensek, semmi olyat nem tesznek, amit Jerry a maga javára tudna fordítani, képesek az egér mozgásától függő összehangolt stratégiát követni. Mindenki pontszerű. Állítás: Jerry kijuthat, kérdés, hogy hogyan? b., rész: A macskák 1,5-szor gyorsabbak. Kijuthat ilyenkor Jerry?
|
| Előzmény: [378] Sirpi, 2006-09-29 13:37:12 |
|
| [390] Cckek | 2006-10-03 21:22:26 |
 Dehogynem. Persze nem akarlak én kioktatni, de minél többet foglalkozol a matematikával, annál egyszerűbbnek fog tűnni. Úgyanakkor bonyólodik is, hisz egyre több kérdést teszel fel. De pont ez a szép benne...:)
|
| Előzmény: [388] Vini, 2006-10-03 21:08:00 |
|
|
|
|
|






