|
| [484] thukaert | 2007-01-27 18:07:31 |
 Így gondolkoztam Lajos
Legyen a három gyök 1,x,y!Tegyük fel hogy a polinom normált!
Ekkor a másodfokú tag együtthatója:
-1-x-y
az első fokú tag együtthatója
x+y+xy
a konstans tag:
-xy
ha ezeket összeadod az -1 és nem gondoltunk a főegyütthatóra ami 1. -1+1=0
|
| Előzmény: [481] Lóczi Lajos, 2007-01-27 17:55:31 |
|
|
| [482] thukaert | 2007-01-27 18:00:16 |
 Íme egy aranyos feladat:
D:=[0,1]x[0,1]
f : D--->D folytonos
Mutassuk meg hogy f-nek van fixpontja!
Ja és Brouwer fixponttételét nem illik felhasználni!
|
|
|
|
|
|
| [477] thukaert | 2007-01-27 16:40:34 |
 Igen,egy harmadfokú polinomegyenletre gondoltam,olyan összefüggés kellene szerintem, amelyben az együtthatók szerepelnek,azok egész kitevős hatványai,és persze az alapműveletek.
|
| Előzmény: [474] Lóczi Lajos, 2007-01-27 15:51:48 |
|
|
|
|
| [473] thukaert | 2007-01-27 15:40:42 |
 Sziasztok!Volna 3 feladat amivel sehogy sem boldogulok, ha valaki tudna segíteni megköszönném
1.Határozzuk meg az n-edik primitív egységgyökök kettős szorzatainak az összegét!
2.Határozzuk meg azon egyenlet együtthatói közötti kapcsolatot, amelynek gyökei egy derékszögű háromszög szinuszaival egyenlők!
3.X,Y n-ed rendű négyzetes mátrixok.Bizonyítsuk be hogy
XY-YX = C megoldható X,Y -ban <=> C nyoma nulla
Előre is köszönöm mindenkinek
|
|
| [472] thukaert | 2007-01-27 14:52:09 |
 A problémára trigonometrikus megoldás is van, bár feleslegesnek tartom, hiszen egyszerűen az
(a+b)(a-b)=a*a-b*b
azonosságot kell felhasználni.
A másik megoldáshoz pedig használd fel a
cos(x/2)=sqrt[(1+cos(x))/2], sin(x/2)=sqrt[(1-cos(x))/2], sin(2x)=2sin(x)cos(x)
azonosságokat, ez szép bár felesleges.
|
| Előzmény: [379] Vini, 2006-10-02 10:00:32 |
|
|
|
|
| [468] Cckek | 2006-12-08 17:09:37 |
 Van-e végtelen sok prímszám, mely három egymásutáni prímszám összege? ilynek pl a 23=5+7+11 vagy a 31=7+11+13
Repetitio est mater studiorum:))
|
|
| [467] Tewu | 2006-12-07 21:19:28 |
 te valami nagyon okos ember lehetsz köszi szépen :D
|
|
| [466] rizsesz | 2006-12-07 21:17:59 |
 x+y=xy=x/y. a második kettőből y négyzete 1, tehát y=1 vagy -1. ha y = 1, akkor pl. az 1. 2 egyenletből x+1=x, ennek nincsen megoldása, ha pedig y=-1, akkor x-1=-x, x=0,5. az egyetlen megoldás a (0,5;-1), x és y szerepe felcserélhető.
|
|
| [465] Tewu | 2006-12-07 21:16:02 |
 Sziasztok! 2 szám összege, szorzata és hányadosa megeggyezik. Melyik ez a 2 szám? lécci lécci valaki segítsen még ma kéne :) köszii előre is jah és eggyenletben kéne felírni
|
|
|
|
|
| [461] ágica | 2006-12-02 13:12:07 |
 Ez egy lineáris diffegyenlet (azaz y'(x)-f(x)y(x)=g(x) alakú), amit úgy oldunk meg, hogy először megkeressük a homogén megoldásokat, azaz az y'(x)-f(x)y(x)=0 egyenlet megoldásait: 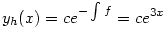 (c valós konstans). Aztán keresünk egy partikuláris megoldást a következő alakban: yp(x)=c(x)e3x (állandók variálásának módszere). Ezt behelyettesítve az eredeti egyenletbe kapjuk, hogy c'(x)=(2x)/(e3x), ahonnan c(x)=-(2+6x)/(9e3x), tehát yp(x)=-(2+6x)/9. Így a diffegyenlet megoldása: y(x) = yh(x)+yp(x) = ce3x-(2+6x)/9. (c valós konstans). Aztán keresünk egy partikuláris megoldást a következő alakban: yp(x)=c(x)e3x (állandók variálásának módszere). Ezt behelyettesítve az eredeti egyenletbe kapjuk, hogy c'(x)=(2x)/(e3x), ahonnan c(x)=-(2+6x)/(9e3x), tehát yp(x)=-(2+6x)/9. Így a diffegyenlet megoldása: y(x) = yh(x)+yp(x) = ce3x-(2+6x)/9.
|
| Előzmény: [460] ., 2006-12-02 11:15:20 |
|




 ), ekkor
), ekkor 


