| [1924] Sinobi | 2017-05-21 13:05:29 |
 Adott egy kör, és rajta kívül két pont. A pontokból érintőket húzunk a körhöz. Igazold, hogy a négy érintési pont a két ponttal egy kúpszeletre esik. Igazold továbbá, hogy ennek a kúpszelet egy pontjából ha a körhöz húzunk érintőt, és így csináljuk a Poncelet tételben szereplő eljárást, akkor 4 lépés után záródik.
(könnyű)
|
|
| [1923] Vonka Vilmos Úr | 2017-04-26 13:40:54 |
 A fókuszok valós eszközökkel is szépen kezelhetőek: kúpszelet fókusza olyan pont, amelyre illeszkedő konjugált egyenespárok pontosan a merőleges egyenespárok.
Komplex módszerekkel is meg lehet őket fogni: az abszolút képzetes körpontokból érintőket húzunk a kúpszelethez, ezek páronként vett további metszéspontjai a fókuszok. Így a két valós fókusz mellett egy képzetes fókuszpár is adódik.
|
| Előzmény: [1922] Sinobi, 2017-04-26 09:42:48 |
|
| [1922] Sinobi | 2017-04-26 09:42:48 |
 Aham. A gyengébb állítás, amelyben két egyenesre kell esniük, az itt található tétel2-nek a Minkowski geometriában való felírása, az erősebb állítás, amelyben az is elég ha kúpszeletre esnek, pedig a de Sitter geometriában (ahol a szög és a távolságmérés is hiperbolikus) való kimondása.
Kúpszeletek fókuszai kezelhetők szépen egyszerűen komplex projektív módszerekkel? (ebben a két geometriában valós projektív eszközökkel is megfoghatók a fókuszpontok)
|
| Előzmény: [1921] Vonka Vilmos Úr, 2017-03-27 08:07:20 |
|
| [1921] Vonka Vilmos Úr | 2017-03-27 08:07:20 |
 Kúpszeletsorokra vonatkozó számolásokkal (amik nem túl nehezek, csak kúpszeletek egyenleteiből kell lineárisan kikombinálgatni a kúpszeletsoruk további kúpszeleteinek egyenletét) egy kicsit általánosabbat is be tudok látni:
Ha adott három kúpszelet úgy, hogy közülük bármely kettőnek két metszéspontja egy negyedik kúpszeleten van (ez most esetünkben egy metsző egyenespár), akkor a további két metszéspont-párok összekötő egyenesei konkurrensek.
De még jó lenne erre valami szebb bizonyítást keresni (szerintem algebrai görbék fokszámát vizsgálva, mint az eredeti "kalapács" esetén a Cayley-Bacharach tételes szép bizonyítás, ki kéne jönnie).
|
| Előzmény: [1920] Sinobi, 2017-03-26 16:09:26 |
|
| [1920] Sinobi | 2017-03-26 16:09:26 |
 Ha a nagy négyzetbe is ellipszist írunk, majd azt dualizáljuk, akkor az előző kalapácshoz nagyon hasonló állítást kapunk: adott két egyenesen 3-3 pont, ezeken át 3 kúpszelet úgy, hogy bármelyik 2-nek 4 metszéspontja legyen, bizonyítsuk be hogy a hatványvonalak 1 ponton mennek át.
Azt hogyan látnád be, ha nem ezt akarnád dualizálni?
(azt ebből tudjuk, hogy mint konfiguráció azonos az előbbi kalapáccsal, vagyis a PG téma 126-ik hozzászólásával, de mondjuk ez nem tűnik fel; meg nem is látom most hogy mi hova kerül)
|
| Előzmény: [1918] Vonka Vilmos Úr, 2017-03-25 17:10:09 |
|
| [1919] Sinobi | 2017-03-25 18:42:14 |
 Kalapács és szög :D Tetszik :)
|
|
| [1918] Vonka Vilmos Úr | 2017-03-25 17:10:09 |
 Na jó, ezt elismerem, hogy kicsit elkapkodtam. (Attól még, hogy a kollineáció az egyik téglalapot a másikba viszi, nem biztos, hogy a beírt kúpszeletet is éppen a tekintett másikba viszi át.)
Újabb próbálkozás:
A másik fórumban beszéltünk a következő állításról: Ha három kúpszeletnek van két közös pontja, akkor a további két-két metszéspontot összekötő egyenesek konkurrensek.
Nézzük ennek az állításnak a duálisát: Ha három kúpszeletnek van két közös érintője, akkor a további két-két közös érintők metszéspontjai kollineárisak.
Legyen most két kúpszeletünk a két beírt ellipszis. A harmadik pedig az az elfajuló másodosztályú görbe, a négyzet két oldalirányának végtelen távoli pontjából áll. A két pontból álló elfajuló másodosztályú görbe érintői a két pontra illeszkedő összes egyenes (ez a metsző egyenespár duálisa).
Erre a három görbére alkalmazva az előbb megfogalmazott duális állítást éppen a feladat állítása adódik.
|
| Előzmény: [1917] Sinobi, 2017-03-25 01:34:01 |
|
|
| [1916] Vonka Vilmos Úr | 2017-03-24 21:58:41 |
 A két befoglaló téglalapnak a négyzet oldalain levő megfelelő csúcsait összekötő egyenesek éppen a négyzet átlóján metszik egymást (ez a Papposz-tételből könnyen látható), legyen ez a közös pont \(\displaystyle C\). Ez azt jelenti, hogy \(\displaystyle C\) centrumú kollineációval át lehet vinni az egyik kis téglalapot a másikba. Ez a kollineáció az egyik téglalapba írt ellipszist a másik téglalapba írt ellipszisbe viszi. Így a közös érintők invariáns egyenesek, vagyis átmennek a \(\displaystyle C\) centrumon.
|
| Előzmény: [1914] Sinobi, 2017-03-24 18:13:28 |
|
|
| [1914] Sinobi | 2017-03-24 18:13:28 |
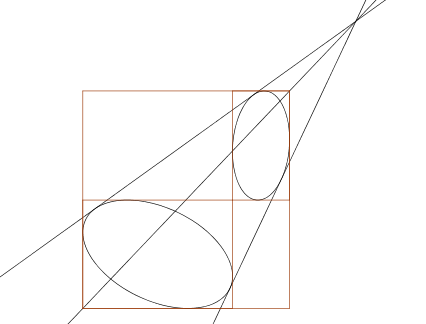
 191. Feladat Egy négyzetet felosztunk 4 részre, két szemközti részbe ellipsziseket írunk az ábra szerint. Bizonyítsd be, hogy a két ellipszis két másik közös érintőjének a metszése a négyzet átlóján van.
|
 |
|
|
| [1912] Cogito | 2016-11-25 22:57:41 |
 A feladatot 1955. január 2-án az alábbi formában adták fel az – akkor még Rákosi Mátyásról elnevezett – Országos Tanulmányi Versenyen:
Egy háromszög belsejében felvett tetszőleges ponton át a háromszög oldalaival párhuzamos egyeneseket húzunk. Ezek az egyenesek a háromszög területét hat részre osztják. Mekkora az adott háromszög területe, ha adva van a keletkezett 3 háromszög területe: \(\displaystyle t_1\), \(\displaystyle t_2\), \(\displaystyle t_3\) ?
Érdemes ezt az általánosított feladatot is megoldani.
|
| Előzmény: [1908] Gergely99, 2016-11-22 21:10:01 |
|
| [1911] Gergely99 | 2016-11-23 23:11:49 |
 Elnézést kérek. Későn esett le a dolog. Nem aktuális a kérdés, és nagyon szépen köszönöm a választ :)
|
|
| [1910] Gergely99 | 2016-11-23 23:03:35 |
 Ez egy lehetséges megoldás lenne, de a feladat nem írta sehol, hogy a háromszög derékszögű. Ezért nem tudtam boldogulni a feladattal. Szóval a kérdés ugyan az, csak annyival kiegészítve, hogy mi van, ha a háromszögem tetszőleges?
|
|
| [1909] jonas | 2016-11-23 14:36:41 |
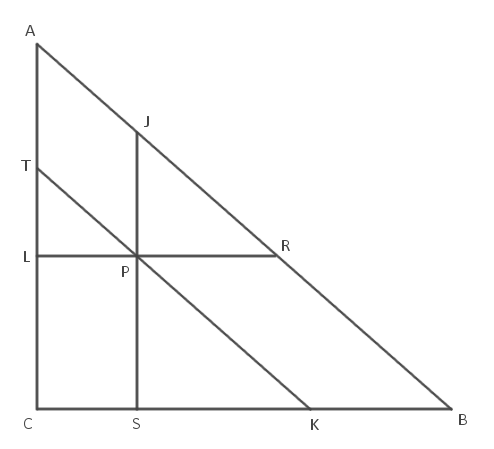
 Legyen a háromszög ABC, a belül felvett pont P. A P ponton át az AB oldallal párhuzamos a BC oldalt K-ban, az CA oldalt T-ben metszi; a BC oldallal párhuzamos az CA oldalt L-ben, az AB oldalt R-ben metszi; végül a CA oldallal párhuzamos az AB oldalt J-ben, a BC oldalt S-ben metszi.
A három kis háromszög, amiről a feladat beszél, PLT, RPJ, KSP. Vedd észre, hogy ez a három háromszög hasonló, mivel minden oldaluk párhuzamos egymással. Ráadásul a BCA háromszög is hasonló az előbbi háromhoz.
Legyen a PLT háromszög területe 1, az RPJ háromszög területe 2, a KSP háromszög területe 3. (Feltehetjük, hogy pont ilyen sorrendben vannak a területek, mert az eredeti háromszög ABC csúcsait betűzhetjük megfelelően.) Mivel az RPJ háromszög hasonló a PLT-hez, de kétszer akkora területű, ezért az oldalai \(\displaystyle \sqrt 2 \)-szer akkorák. Hasonlóan a KSP háromszög oldalai \(\displaystyle \sqrt 3 \)-szor akkorák, mint a PLT-é.
Mivel párhuzamosokat húztunk, a PJAT négyszög paralelogramma, így a TA szakasz hossza megegyezik a PJ szakasz hosszával, ez utóbbiról pedig a PLT és RPJ háromszögekből tudjuk, hogy \(\displaystyle \sqrt 2 \)-szer akkora, mint az LT szakasz. Hasonlóan PSCL is paralellogramma, így az LC ugyanolyan hosszú mint a PS szakasz, ez pedig \(\displaystyle \sqrt 3 \)-szor olyan hosszú, mint az LT szakasz.
Mármost mivel P a háromszög belső pontja, és PL párhuzamos BC-vel, ezért L a BC szakasz belső pontja. Hasonlóan PT párhuzamos AB-vel, ez pedig egy egyenesbe esik AR-rel, P pedig R és L között van, ezért T az AL szakasz belsejében van.
Ezekből az LA szakaszt a T belső pont az TA és a LT szakszra bontja, amik közül az AT-ről már megállapítottuk, hogy \(\displaystyle \sqrt 2 \)-szer olyan hosszú, mint LT, így az LA szakasz \(\displaystyle \sqrt 2 + 1 \)-szer olyan hosszú, mint LT. Hasonlóan a CA szakaszt L felbontja az LA és LC szakaszra, ezért a CA szakasz \(\displaystyle \sqrt 2 + 1 + \sqrt 3 \)-szor olyan hosszú, mint LT. Viszont a BCA háromszög hasonló a PLT háromszöghöz, és az utóbbinak a területe 1, ezért az oldalak arányából az előbbinek a területe \(\displaystyle (\sqrt2 + 1 + \sqrt3)^2 \), ami körülbelül 19.17.
|
 |
| Előzmény: [1908] Gergely99, 2016-11-22 21:10:01 |
|
| [1908] Gergely99 | 2016-11-22 21:10:01 |
 Jó estét kívánok mindenkinek!
Volna egy olyan feladatom, aminek nem tudom, hogy hogyan álljak neki, de szeretném nagyon megoldani. Pusztán kíváncsiságból szeretném megtudni, hogy hogyan kellene a feladatot megoldani.
Ez lenne a feladat:
Egy háromszög belsejében felvett ponton át a háromszög oldalaival párhuzamos egyeneseket húzunk. Ezek az egyenesek a háromszöget 6 részre osztják. Mekkora az eredeti háromszög területe, ha a keletkezett 3 háromszög területe: 1, 2 illetve 3 egység?
|
|
| [1907] Dömötör Erzsi | 2016-10-28 23:19:25 |
 Talán nem tartjátok OFF-nak a témát, ha nem a geometria szépségeiről írok, hanem arról, aki e fórum keretein belül olyan sok gondolatát megosztotta velünk :(
|
 |
|
| [1906] jonas | 2016-10-14 15:16:25 |
 Forgassuk el az \(\displaystyle SQ \) szakaszt derékszöggel, és toljuk el, hogy az egyik végpontja \(\displaystyle P \)-be kerüljön, így kapjuk a \(\displaystyle PT \) szakaszt. A kulcs észrevétel, hogy az \(\displaystyle RT \) egyenes megegyezik a négyzet \(\displaystyle CD \) oldalegyenesével. A másik három oldalegyenest úgy kapjuk, hogy \(\displaystyle P \)-n át párhuzamost húzunk \(\displaystyle RT \)-vel, majd \(\displaystyle Q \)-n és \(\displaystyle S \)-en át merőlegest \(\displaystyle RT \)-vel.
Csakhogy ebben a szerkesztésben a \(\displaystyle T \) pontra két lehetőséget kapunk a szerint, hogy az elforgatott szakasz melyik végpontja kerül \(\displaystyle P \)-be. A két lehetőség két ellentétes körüljárású négyzetet ad.
Speciális esetek. Ha \(\displaystyle R = T \), de \(\displaystyle P \ne T \), akkor van végtelen sok különböző négyzet, mégpedig bármilyen irányú oldalegyeneshez egy, kivéve a \(\displaystyle PR \)-rel párhuzamos vagy merőleges irányt. Ha \(\displaystyle PTR \) kollineáris, de \(\displaystyle R \ne T \), akkor nincs megoldás.
Ha a feladatkiírást úgy értelmezed, hogy \(\displaystyle P \) az \(\displaystyle AB \) szakaszon legyen stb, akkor minden megoldást ellenőrizni kell, hogy az adott pontok tényleg a szakaszokon vannak, nem az oldalegyenesek valamely másik részén. Ekkor a tipikus esetben legfeljebb egy megoldás lehet.
|
| Előzmény: [1905] w, 2016-10-13 18:46:54 |
|
| [1905] w | 2016-10-13 18:46:54 |
 Adottak a síkon a \(\displaystyle P,Q,R,S\) pontok. Szerkesszünk olyan \(\displaystyle ABCD\) négyzetet, melyre \(\displaystyle P\in AB\), \(\displaystyle Q\in BC\), \(\displaystyle R\in CD\), \(\displaystyle S\in DA\)!
|
|
| [1904] Sinobi | 2016-07-27 00:31:12 |
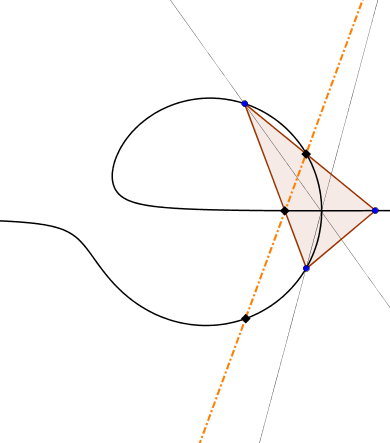
 189. feladat: Legyen &tex;\displaystyle \vartheta&xet; két, közös végpontú szakasz, HI és IJ ekvioptikus görbéje (azaz: azon P pontok mértani helye, melyekre HPJ egyik szögfelezője átmegy I-n)
Bizonyítsuk be, hogy ha A,B,C &tex;\displaystyle \in \vartheta&xet; háromszög a görbén fekszik úgy, hogy ABC beírt körének középpontja I, akkor EFG egy egyenesre illeszkednek, amennyiben &tex;\displaystyle \{E,F,G\} = ABC \cap \vartheta&xet; A,B,C-tól különböző metszéspontjai.
|
 |
|
| [1903] Sinobi | 2016-05-30 13:42:45 |
 > Adott a síkon négy egyenes. Tekintsük az összes kúpszeletet, amelyek érintik ezt a négy egyenest. Mi az ilyen tulajdonságú kúpszeletek középpontjának mértani helye?
Ezt is én, nem lett megoldva (számozni kéne??). A válasz az hogy a Newton érintőnégyszög tétele értelmében az átlók felezőpontjait összekötő egyenesen lesz. (Ellipszisre úgy megy, hogy körré affinítod, és alkalmazod Newton tételét. Hiperbolára mondjuk úgy, hogy veszed ugyanazt a bizonyítást a Minkowski síkon, és megkapod derékszögű hiperbolára a tételt. Másik lehetőség, hogy tükrözöl a kúpszelet középpontjára, és akkor a Brianchon azonnal adja.) (.. minden testre működik ez a bizonyítás, nem? Létezik 4 egyeneshez mindig érintő kúpszelet, kúpszeletnek középpont, középpontnak tükrözés, illetve Brianchon..?)
.. mi a helyzet magasabb dimenzióban? Két adott másodrendű felület lineáris kombinációnak a középpontjainak mi a mértani helye? N síkot érintő másodrendű felületek középpontjainak?
(Én nem tudom.)
.. van valakinek szakirodalma másodrendű felületsorokról?
|
| Előzmény: [1776] Sinobi, 2013-12-11 18:15:18 |
|
| [1902] Sinobi | 2016-05-26 03:49:47 |
 >> Kúpszeletsor középpontjának mértani helye?
> Sejtés: a négy megadott pont (A,B,C,D) által meghatározott összes szakasz felezőpontjára illeszthető kúpszelet.
Egy geometriai megoldás:
Ha a négy pont konkáv, akkor egy ortogonális négyesbe affinítod őket. Ekkor az összes rajtuk átmenő kúpszelet merőleges parabola lesz, és a középpontjuk a négyszög Feuerbach-körén lesz. Ezt nem nehéz belátni.
Ha a négy pontod konvex, akkor húrnégyszöggé affinítod, és, még sokkal egyszerűbben be lehet látni hogy az ilyen középpontok mértani helye egy merőleges hipike. (Nagyon érdemes észben tartani, hogy merőleges hipikét kapsz akkor ha egy sugársort csúsztatva tükrözöl és elmetszel önmagával, és általában csak ilyenkor.)
(Ha a négy pont trapéz akkor közelíted nem trapézokkal, a mértani hely is folytonosan fog változni.)
Ez egy nagyon erős és jól használható módszer, érdemes észbentartani. (Nem is gondolná az ember, hogy mi minden affin/vektoros, ami elsőre nem tűnik annak.)
|
| Előzmény: [1750] w, 2013-10-30 22:24:46 |
|
|
| [1900] sakkmath | 2016-03-14 20:46:35 |
 A 188. feladat a 185. köpönyegéből bújt elő, ezért HoA [1899]-es szép megoldása - átbetűzések után - megoldja 188-at is.
Utóbbira felteszek egy új megoldást, amely a Casey-tételkört érinti oda-vissza. Egyúttal köszönöm W-nek, hogy a témáról alapos összegzést adott [1894]-[1895]-ben.
|
 |
|