|
| [2357] epsilon | 2007-10-06 08:57:35 |
 Helló! A következő kérdésre nem találok azonnali választ :-( "Ihazoljuk, hogy minden nemnegatív n egész szám esetén 8n+10 felírható két páratlan egész szám négyzetösszegeként!" Bármilyen tippet előre is köszönök! Üdv: epsilon
|
|
|
| [2354] rizsesz | 2007-10-02 15:18:11 |
 Ezekből az egyenletekből páronként 2x=y+z, 2y=x+z, 2z=x+y, és ezekből x=y=z könnyen jön, ami valóban az említett egyenes. nem :D?
|
|
| [2353] SmallPotato | 2007-10-02 14:29:53 |
 "Egy kocka 3 kitérő élétől egyenlő távolságra levő pontok halmaza micsoda?"
Erős meggyőződésem szerint a kérdéses mértani hely egy egyenes. Konkrétan az az egyenes, amely tartalmazza a kockának azon (egyetlen) testátlóját, amely mindhárom jelzett kitérő élhez képest kitérő.
Bizonyítani sajnos nem tudom. :-(
Eljutottam egy ilyen, a kérdéses mértani hely (x,y,z) pontjait leíró egyenletrendszerhez (a kocka élhossza 2a, élei a koordinátatengelyekkel párhuzamosak, középpontja az origóban):
(a-y)2+(a+z)2 = (a-z)2+(a+x)2 = (a-x)2+(a+y)2
Ennek a jelzett egyenes pontjai valóban eleget tesznek - de elvben talán más pontok is? Nem tudom.
|
| Előzmény: [2255] rizsesz, 2007-09-02 20:52:05 |
|
|
| [2351] nadorp | 2007-10-01 09:45:33 |
 Köszönöm a hozzászólásokat. Én Lóczi Lajoshoz hasonlóan csináltam. A sin(x+15o)=sin18o egyenletnek a 3o és 147o a megoldása. Ez a sin xcos15o+cos xsin15o=sin18o egyenletre vezet. Ebből sin x-re egy másodfokú egyenletet kapunk, aminek a kisebbik gyöke sin3o
|
|
|
| [2349] SmallPotato | 2007-09-30 23:48:36 |
 A 18 fokos szög szögfüggvényeinek megállapításához (a készen kapható ötleteken kívül, persze) a 72-72-36 fokos szögekkel bíró egyenlőszárú háromszöget javaslom; ennek oldalarányai (ha ugyan fejből nem ismertek :-) ) annak felismerésével határozhatók meg, hogy az egyik 72 fokos szög felezője a szemközti oldalból saját magával azonos hosszúságú szakaszt metsz ki, a másik metszék pedig egy újonnan keletkezett kisebb, szintén 72-72-36 fokos háromszög legkisebb oldala.
|
| Előzmény: [2348] SmallPotato, 2007-09-30 23:40:47 |
|
|
| [2347] Lóczi Lajos | 2007-09-30 23:13:51 |
 [Nyilván 3=18-15, és a félszögképlet miatt csak a 18 fok szinuszán kell kicsit gondolkodni, de a példatárakban (pl. Geom. feladatgyűjtemény) az aranymetszésnél ez utóbbi szög szinusza is ki van számolva (Mathematica alatt: Sin[3 Degree] // FunctionExpand, weben (még egy felezésre szükség van): http://functions.wolfram.com/ElementaryFunctions/Sin/03/02/).]
|
| Előzmény: [2344] nadorp, 2007-09-30 20:05:12 |
|
|
|
| [2344] nadorp | 2007-09-30 20:05:12 |
 határozzik meg sin 3o pontos értékét középiskolai módszerekkel
|
|
|
|
| [2341] epsilon | 2007-09-30 16:27:08 |
 Bocs, hogy így szotyogtatom, ez még kijött, és az a sejtésem, hogy a 2 eset eredményeit kapjuk más n számok esetén is de, hogy mikor melyiket, még nem látom :-(
|
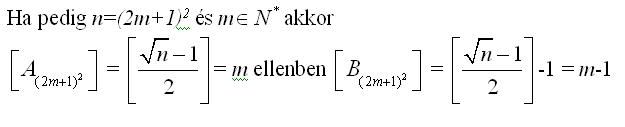 |
|
| [2340] epsilon | 2007-09-30 16:03:04 |
 Ha nem tévedtem, akkor az egészrészes eredmény páros teljes négyzet esetén mégis igaz, vagyis:
|
 |
|
| [2339] epsilon | 2007-09-30 15:26:31 |
 Igen, valóban erre sem jó, Én kicsi teljes négyzetekre, majd n=100 értékére próbáltam, ezekből próbáltam arra következtetni amit írtam, de hibásan :-( Végül is az érdekelne, hogy egyenlőek-e az An és Bn egészrészei, és mivel is egyenlőek ezek, ha n>=2 pozitív egész, és:
|
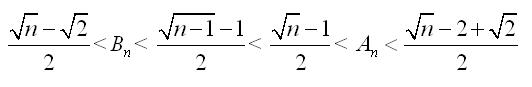 |
|
|
| [2337] epsilon | 2007-09-30 14:31:32 |
 Bocs, az egészrész nem az, és az egyenlőtlenségeket is megnézem, ha valamit elszámoltam volna.Továbbá n>2. Az egészrészes ez kell legye:
|
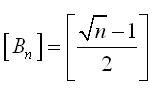 |
|
|
| [2335] epsilon | 2007-09-30 11:18:35 |
 Tisztelt Kollégák! Egy érdekes egyenlőtlenseég vezetett a következő kérdéshez: ha fennáll a következő egyenlőtlenséglánc, akkor igaz-e az egészrészre vonatkozó eredmény? Ha n négyzetszám, akkor Nekem kijött, de általában?Előre is köszönöm a válaszotokat!
|
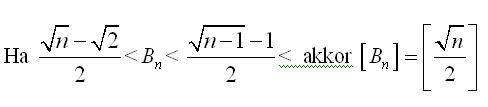 |
|
| [2334] Lbandi | 2007-09-28 20:49:15 |
 Köszönöm a válaszokat, tényleg elég nehéznek tűnik paraméteresen megadni a megoldást, egy kicsit hanyagul megfogalmazott a feladat evvel a "mi lehet lnko(x,y)?"-nal.
|
|
| [2333] Hajba Károly | 2007-09-28 00:42:05 |
 Valóban. Tegnap már nagyon késő volt és egy mondat még lemaradt. A több megoldás közül melyikre keresed az lnko-t, mert szerintem a, b, c paraméteres ismeretében ez nem egyszerű feladat.
De nézzünk egy kokrét példát:
3x+5y=61
x:y = 2:11; 7:8; 12:5 és 17:2 ha a pozitív eredményeket tekintjük. Tehát elég bonyolult függvény adhatja meg paraméteresen lnko(x,y) lehetséges értékeit.
Kicsit továbbgondoltam a feladatot, pontosabban azt, hogy mikor megoldható az alapegyenlet. Úgy tűnik, két esetben nincs megoldhatóság:
Ha (a=b)&(c 2*n*a) ill. ha páros(a,b)&páratlan(c) 2*n*a) ill. ha páros(a,b)&páratlan(c)
|
| Előzmény: [2331] Lbandi, 2007-09-27 08:56:05 |
|







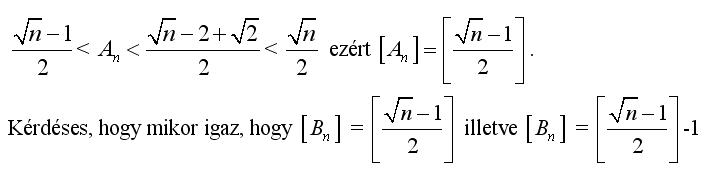
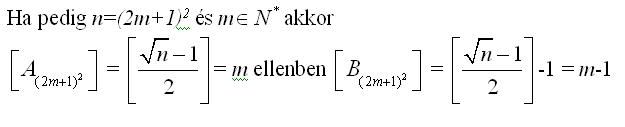

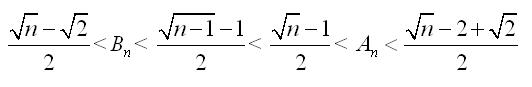
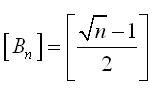
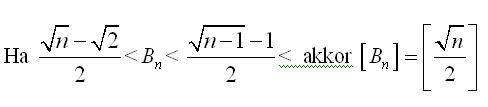

 2*n*a) ill. ha páros(a,b)&páratlan(c)
2*n*a) ill. ha páros(a,b)&páratlan(c)