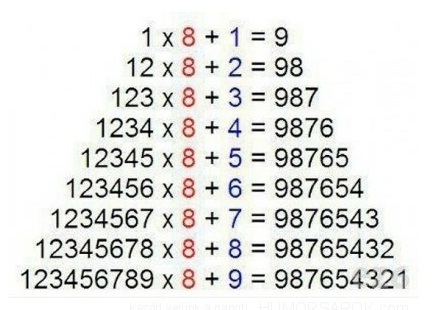|
| [3567] Lóczi Lajos | 2012-05-25 02:12:15 |
 Keressünk minél nagyobb olyan valós x számot, melyhez megadhatók alkalmas y és z valós számok, hogy az
x8+2y8+3z8 1 és x3+7z3 1 és x3+7z3 3+9y3 3+9y3
egyenlőtlenségek fennállnak.
|
|
|
| [3565] jonas | 2012-05-07 20:29:50 |
 Hát, ha senki nem vállalja, itt a gyors magyarázat.
Vegyünk egy olyan számot, mint
t=1234567.
Ha ezt megszorozzuk tízzel, akkor ugyanazt a sort kapjuk, csak eltolva.
10t=12345670.
Most vonjuk ki egymásból a kettőt. A szemléletesség kedvéért illesszük egymás alá a számjegyeket, így jobban látszik:
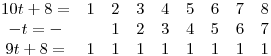
Az utolsó kivételével minden helyiértéken két szomszédos számjegyet vonunk ki az eredeti számban, és ebből a két szomszédos számjegyből az első eggyel nagyobb, így mindenhol 1 lesz a különbség. (Az utolsó helyiértéknél csaljunk egy kicsit.)
Most vonjunk ki t-t még egyszer:
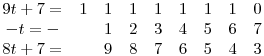
Ezt úgy kell elképzelni, hogy a t minden számjegyét a 9t+7 eggyel nagyobb helyiértéken lévő számjegyéből vonjuk ki, tehát mindegyik számjegyet 10-ből. Így a 10-ből sorra kivonjuk a számokat 1-től valameddigig, ezért az eredmények sorra 9-től mennek egyesével lefelé.
Természetesen ugyanez megy 16-os számrendszerben is:
E16.1234567816+816=FEDCBA9816.
E16.12345678916+916=FEDCBA98716.
E16.123456789A16+A16=FEDCBA987616.
|
| Előzmény: [3564] lorantfy, 2012-05-05 14:02:27 |
|
| [3564] lorantfy | 2012-05-05 14:02:27 |
 Adjatok erre egy gyors magyarázatot! Megy ez 16-os számrendszerben is?
|
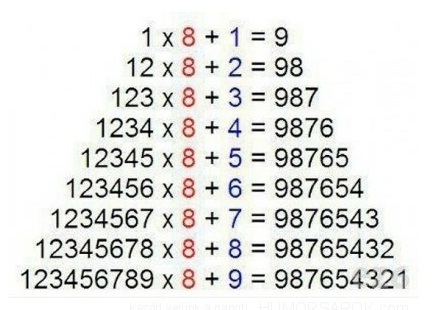 |
|
| [3563] Fálesz Mihály | 2012-04-23 10:19:11 |
 Alapvetően Attilával értek egyet. A feladattal a baj a kérdésben levő visszacsatolás. A helyes válasz attól függ, hogy mi a helyes válasz.
Számtalan ilyen logikai paradoxon ismert. Ha ez az állítás igaz, akkor én vagyok a Mikulás. Mi a legkisebb pozitív egész, amit nem lehet 1000-nél kevesebb karakterrel definiálni?
Az adott kérdésben a 0 az egyetlen "stabil" válasz, de lehetne próbálkozni a 0/25/25/50 (nincs stabil válasz) vagy a 25/75/75/75 (a 0, 25 és a 75 is stabil) változatokkal is...
* * *
Ha az "én most nem mondok igazat" mondatba beleteszünk egy kis elektronikus késleltetést, akkor hívhatjuk astabil multivibrátornak. :-)
|
|
|
| [3561] lorantfy | 2012-04-22 19:49:21 |
 Szerintem nem kell ahhoz 100 emberrel megoldatnunk a feladatot, hogy tudjuk, az A, B, C, D lehetőségek közül véletlenül kiválasztva egyet 1/4 lesz a kiválasztás esélye. Mivel véletlenszerűen választunk nem is nézzük meg milyen számokat takarnak ezek a válaszok. Négy egyforma boríték közül választunk, melyekben egy papíron ott vannak az adott számok. Mit jelent az, hogy helyes a választásod? Azt, hogy kinyitva a borítékot amit választottál, olyan szám lesz benne, amilyen valószínűséggel kiválaszthattad éppen azt a számot. A feladatban viszont látjuk ezeket a számokat és éppen az okozza az ellentmondást, hogy egyik értéke sem egyezik meg azzal az eséllyel amivel ő maga kiválasztható. A kérdés szerintem feltehető, és lenne is jó válasz a kérdésre, ha a válaszok pl.ezek lennének? A)15 B)50 C)35 D)50 Ekkor az 50 jó válasz lenne. (A százalékokat az ismert okok miatt elhagytam.)
|
| Előzmény: [3558] jenei.attila, 2012-04-22 18:08:49 |
|
| [3560] SmallPotato | 2012-04-22 19:19:05 |
 Javítás az elveszett végű bekezdéshez.
... Ha a 25 % pontosan egyszer szerepelne a helyes adatok között, akkor korrekt válasz lenne adható. A kérdés egy valószínűség, ami a kedvező és az összes esetek számának konkrét ismeretében egyértelműen eldönthető.
|
| Előzmény: [3559] SmallPotato, 2012-04-22 19:14:48 |
|
| [3559] SmallPotato | 2012-04-22 19:14:48 |
 "Bármi más válaszok lennének, akkor is értelmetlen lenne a kérdés."
"A baj az, hogy a kérdés maga értelmetlen, ... nem lehet rá igennel vagy nemmel válaszolni"
Szerintem a kérdés egyáltalán nem értelmetlen. "Ha véletlenszerűen kiválasztasz egy választ, mi az esélye, hogy a helyeset választottad?" Ha a 25
A dolgozatos példádhoz: egy valószínűséget nem lehet (de nem is kell hogy lehessen) egyetlen elemből álló minta várható értékéből megjósolni. (100 dolgozat persze az eredeti kérdésre szintén nem adná meg a választ.)
|
| Előzmény: [3558] jenei.attila, 2012-04-22 18:08:49 |
|
| [3558] jenei.attila | 2012-04-22 18:08:49 |
 Véleményem szerint ennek a feladatnak egész más baja van, mint hogy kétszer szerepel benne a 25 százalék és egyszer az 50 százalék. Bármi más válaszok lennének, akkor is értelmetlen lenne a kérdés. Képzeljük el, hogy 100 emberrel megoldatjuk a feladatot, majd elkezdjük kijavítani a dolgozatokat. Ha 25 százalék a helyes válasz, akkor várhatóan 25 helyes megoldás lesz. De mi a helyes megoldás az első dolgozat javításakor? Már egy dolgozatnál is el kellene tudni dönteni, hogy az adott válasz helyes-e vagy nem. A baj az, hogy a kérdés maga értelmetlen, abban az értelemben, hogy nincs igazságtartalma (nem lehet rá igennel vagy nemmel válaszolni). Ez kb. olyan, mintha azt kérdeznénk: "ez a kérdés igaz?". Önmagáról kérdez (vagy állít) valamit, aminek egyszerűen nincs igazságtartalma. Az ilyen állítások nem megengedhetők. Leginkább talán a Russel paradoxonhoz hasonlít, ami abból adódik, hogy nem lehet "ész nélkül" halmazokat kreálni. Vagy pl. az "ez a mondat hamis" állítás sem igazi állítás, ezért értelmetlen megkérdezni, hogy igaz-e vagy sem. Tehát a feladat sokkal inkább logikai mintsem valószínűségszámítási. Egyébként érdekes feladat, mondjátok el a véleményeteket róla.
|
| Előzmény: [3556] lorantfy, 2012-04-20 22:37:01 |
|
| [3557] HaliPeu | 2012-04-21 15:54:28 |
 Szerintem a megoldás 0, mert az pont nullaszor szerepel, ezért 0
|
|
| [3556] lorantfy | 2012-04-20 22:37:01 |
 Egy jó választ kell kiválasztanunk a 4 közül, ennek az esélye 0,25. Tehát a jó válasz a 0,25. Ebből viszont kettő van, így a kiválasztásának esélye 0,50. Vagyis a jó válasz az 0,50. Ebből viszont csak 1 van, így a véletlen kiválasztás esélye 0,25... Szóval paradoxon. Akkor lenne megoldása, ha a 0,25 egyszer vagy az 0,50 kétszer szerepelne, de egyszerre csak az egyik.
|
| Előzmény: [3552] Hajba Károly, 2012-04-14 19:44:58 |
|
|
|
|
|
|
|
|
|
| [3547] jonas | 2012-01-15 13:13:49 |
 Épp ellenkezőleg. Hasznos, hogy elmondtad, hogy lehet megtalálni egyszerűen ezt a megoldást. Én egyszerűen csak végignéztem az összes kis számot, hogy melyik működik. Mivel azt írtad, hogy van 800 alatt megoldás, ezért kezdtem el kis példát keresni.
|
| Előzmény: [3546] FlagD, 2012-01-15 13:07:44 |
|
| [3546] FlagD | 2012-01-15 13:07:44 |
 Akkor én is lelövöm az én "megoldásom".A két számot a-val, és b-vel fogom jelölni. b=a+k (vagyis a és b között k-1 darab számra kell teljesülnie a feltételnek.)
Az első, ami beugrott, az az ismert feladat, hogy bármely pozitív egész n-re van egymás utáni n darab összetett szám. 6!+1=721 pedig osztható 7-tel, vagyis a=6!, és b=6!+7 jó választás lesz. Azt néztem el, hogy 727 persze nem osztható 7-tel. (No persze annak is be kellett volna ugrani, hogy Wilson-tétele miatt,akkor már pl. 5|4!+1 is igaz, és a=4! is hasonló okok miatt nem megfelelő)
És akkor, hogy lehet jó megoldást adni: Az könnyen látható, hogy a,b>2. Mivel két szomszédos szám legnagyobb közös osztója : (n;n+1)=1, emiatt (a;b-1)>1, és (b;a+1)>1 (és így a-nak, és b-nek kell lennie különböző prímosztójának ). Ha elkezdjük b-1;a-val, illetve b;a+1-gyel az euklideszi-algoritmust, akkor mindkét esetben az első maradék: k-1. Ez a fentiek miatt azt jelenti, hogy k-1-nek legalább két különböző prímosztója van. Nézzük sorba az eseteket (amikor pontosan két prímosztója van k-1-nek!)
1. Ha k-1=2*3. Ekkor b=a+7. (Legyen most 2|a, és 3|b; a fordított eset hasonló!) Ekkor a+1 (=b-6 miatt!); a+2; a+4 (=b-3 is!); a+6 számok "jók", de a+3=b-4 mind a-val, mind b-vel relatív prím. Vagyis ez az eset nem lehet!
2-3. Hasonlóan k-1=2*7 (2|a,7|b) esetre pedig a+7=b-8 "rossz"; míg k-1=2*5 (2|a,5|b) esetre: a+5=b-6 "rossz", amennyiben 3 nem osztója b-nek, és a+9=b-2 "rossz", amennyiben 3 nem osztója a-nak (és persze 3 vagy a-t, vagy b-t oszthatja csak!)
4. Legyen most k-1=3*5 (itt lesz a jó megoldás), illetve 3|a, 5|b! Válasszuk a-t párosnak is (ekkor persze b is az). Így a+1(=b-15 miatt), a+2, a+3,a+4;a+6(=b-10 miatt is);a+8;a+9;a+10;a+11(=b-5 miatt);a+12;a+14;a+15 eleve "jók" (a,és b választása miatt). a+5=b-11; a+7=b-9; a+13=b-3 számokat kell vizsgálnunk csak. Mivel 3 nem osztja b-t, 5 pedig a-t, a fenti három vizsgált szám csak úgy lehet "jó", ha 11|b, míg 7*13|a teljesül. Most ott tartunk, hogy 2*3*7*13=546|a , míg 2*5*11=110|b. Vegyük észre, hogy 5*2*5*11=550 "közel" van 546-hoz. Ha mind 546-t, mind 550-t szorozzuk 4-gyel, akkor megfelelő a-t, b-t kapunk. Vagyis a=2*2*2*3*7*13 = 2184 , és b=2*2*5*5*11 = 2200 valóban jó választás.
Azt még nem látom pontosan, hogy miért ez a legkisebb. Ja és elnézést jonastól (természetesesn Övé az érdem), hogy lelőttem, hogy a megoldása hogy jöhetett ki, a rossz megoldásom miatt próbáltam "kiköszörülni a csorbát"!
Üdv!
|
| Előzmény: [3545] jonas, 2012-01-15 11:16:07 |
|
|
| [3544] jonas | 2012-01-15 11:09:56 |
 Esetleg úgy érted, olyat találtál, ahol a két szám különbsége van 700 és 800 között? Mert olyan megoldás biztosan nincsen, ahol mindkét szám 800 alatt van.
|
| Előzmény: [3543] FlagD, 2012-01-15 10:14:46 |
|




 1 és x3+7z3
1 és x3+7z3 3+9y3
3+9y3