|
| [101] SmallPotato | 2009-01-07 18:17:55 |
 Csak egy ötlet (nem számoltam utána): mi lenne, ha az ábrádon látható 4 db 120 fokos kereszteződést (ezek egy négyzet csúcsain vannak ugye) a leni538-féle, a 92. hsz-ben adott módon kötnénk össze? Ez automatikusan tartalmazná a középső pontot is, és rövidebb lenne a 90 fokos változatnál.
|
| Előzmény: [96] Sirpi, 2009-01-07 15:06:34 |
|
| [100] Sirpi | 2009-01-07 17:36:22 |
 Ez nem hangzik rosszul. Viszont extra kereszteződésből nem lehet nagyon sok, legyen belőlük k. A 9 csúcs mindegyike legalább elsőfokú, az extra csúcsok pedig garantáltan 3-adfokúak, különben el lehet őket hagyni. A csúcsok száma 9+k, és mivel fáról van szó, az élek száma 8+k. Másrészt a fokszámokra adott alsó becslések összegének fele mindenképp alulról becsli az élek számát, tehát:
(9+3k)/2 8+k 8+k
Innen k 7, legfeljebb ennyi extra kereszteződés lehet a minimális összhosszú hálózatban (általában, n terminál-csúcs esetén is igaz, hogy (n+3k)/2 7, legfeljebb ennyi extra kereszteződés lehet a minimális összhosszú hálózatban (általában, n terminál-csúcs esetén is igaz, hogy (n+3k)/2 n+k-1, ahonnan k n+k-1, ahonnan k n-2). n-2).
|
| Előzmény: [98] Csimby, 2009-01-07 16:36:50 |
|
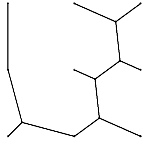
| [99] leni536 | 2009-01-07 17:20:01 |
 Sirpi: Ha a közepét kijavítod, akkor ugyanazt az úthosszt kapod, mint jonas.
Én találtam egyet, ami egész jó, de még mindíg csak kb. 7,55-öt tud.
|
 |
| Előzmény: [96] Sirpi, 2009-01-07 15:06:34 |
|
| [98] Csimby | 2009-01-07 16:36:50 |
 Szerintem erre lehetne írni programot ami megközelítőleg megoldaná. Itt található egy jegyzet: http://www.cs.elte.hu/ frank/jegyzet/kombalg.ps 31.oldalon az 5.példa dinamikus programozásra a Steiner fa probléma. Arról szól hogy adott egy G irányítatlan gráf. Minden élnek van egy költsége. Illetve ki van jelölve csúcsoknak egy T halmaza (terminálok). És olyan minimális költségű összefüggő részgráfot keresünk, mely tartalmazza a terminál csúcsokat. Az algoritmus ami itt szerepel a gráf csúcsszámában polinomiális idejű, |T|-ben exponenciális, de az most mindegy, mert jelen esetben |T|=9 konstans. És akkor lehetne azt csinálni hogy csinálunk egy jó sűrű beosztást (mondjuk 100 egyenlő részre osztjuk az egységet, ekkor lesz 40000 "rácspontunk", mindegyiknek megfeleltetjük a gráf egy csúcsát), bármely két csúcs között menjen él és a költsége legyen a két pont távolsága (a koordinátákból Pit. tétellel gyorsan számoolható). Akkor az algoritmus megadná a legrövidebb úthálózatot melyben az út szakaszok végpontjai e közül a 40000 rácspont közül kerülnek ki, ez szerintem már elég finom lenne, hogy megsejtsünk valamit (pl. hogy az eddig megtalált megoldás az optimális). Ma reggel vizsgáztam ebből a tárgyból, azért is jutott eszembe, meg ezért is vagyok fáradt és néztem be a Sin/Cos-t az előbb :-P
|
|
|
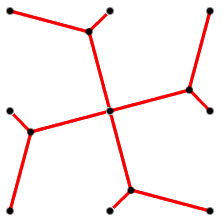
| [96] Sirpi | 2009-01-07 15:06:34 |
 Na, az nem lenne rossz.
Én is kb. arra jutottam, mint amiket eddig írtatok (kivéve ezt az új legjobb eredményt). Ezt a képet azért beteszem, mert annyi mindenképp látszik belőle, hogy ez a 4.1,93 7,72-es (nem túl jó) eredmény tovább javítható, hiszen vannak benne 90o-os szögek, amiket ha kicserélünk egy 120o-os 3-as útkereszteződésre, akkor a széleken változik meg a szög így ott lehet tovább javítani stb. Bár azt ki kellene számolni, hogy ennek az ábrának a javítás utáni "határértéke" milyen eredményt ad. 7,72-es (nem túl jó) eredmény tovább javítható, hiszen vannak benne 90o-os szögek, amiket ha kicserélünk egy 120o-os 3-as útkereszteződésre, akkor a széleken változik meg a szög így ott lehet tovább javítani stb. Bár azt ki kellene számolni, hogy ennek az ábrának a javítás utáni "határértéke" milyen eredményt ad.
|
 |
| Előzmény: [95] Csimby, 2009-01-07 14:32:42 |
|
|
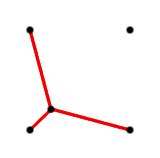
| [94] jonas | 2009-01-06 22:32:49 |
 Másrészt vegyük észre, hogy ha egy négyzetnek csak három csúcsát kell összekötni, akkor ezt 1.93185 hosszúságú úttal megtehetjük. Ez lehet, hogy segít a nehezebb feladatban.
|
 |
|
|
|
| [91] Sirpi | 2009-01-06 16:09:19 |
 Kezdeném egy egyszerű feladattal:
Adott 4 város, egy négyzet négy csúcsában, a négyzet oldala 1km. Mennyi a minimális úthálózat hossza, ha el akarunk jutni bármely városból bármely másikba? Értelemszerűen beiktathatunk további kereszteződéseket.
Ezután pedig az igazi kérdés: Mennyi a minimális úthálózat hossza, ha 9 városunk van egy 3x3-as rácsba rendezve és a szomszédos városok távolsága 1km?
|
|
|
|
|
|
|
|
| [84] Hajba Károly | 2008-10-14 19:01:50 |
 Középen van és alul érint. Nincs forgatva és vízszintesen eltolva, mert azok két oldalt is csökkentenek. Az ilyen faladatok legjobb megoldása sokszor lokális szimmetriát igényel. Talán vizsgálatm a fölfelé eltolást, de már nem emlékszem. Ez már akkor megvolt, amikor föltettem. Másrészt, ha más változókat is behozok, rengeteg esetet kellene megvizsgálnom, s erre sem időm, sem idegrendszerem nincs. Egy elmozdításból következő változások végig vitele rossz esetben pár percig is eltarthat. Így általában a megérzésem után a legcélravezetőbbnek tűnő irányban haladok. Tisztában vagyok vele persze, hogy ezzel bizony akár a jó megoldás mellett szépen el is mehetek.
|
| Előzmény: [83] jonas, 2008-10-14 17:59:13 |
|
| [83] jonas | 2008-10-14 17:59:13 |
 Itt a kék rész középre van igazítva, vagy lokálisan is elmozgattad úgy, hogy a kapott terület maximális legyen? Három szabadsági foka van, valahogy talán lehet javítani, csak akkor az alakja is nagyon ronda lesz.
|
| Előzmény: [74] Hajba Károly, 2008-10-14 17:24:55 |
|
|
|
| [80] jonas | 2008-10-14 17:42:53 |
 A magasságot én körülbelül 0.260147-nek választanám, mert valahol itt maximális, itt a terület 0.292354, aminek a háromszorosa 0.877061.
|
|
|
| [78] Sirpi | 2008-10-14 17:32:32 |
 Igen, így tényleg jobb, akkor az enyém sztornó :-)
Viszont Jonas 0.2918-at írt 1/4-es magasság mellett az előző ötletemre, az 3-mal felszorozva 0.8754, lehet, hogy máshogy választva meg a vastagságot kijön belőle még 0.003-as növelés...
|
| Előzmény: [74] Hajba Károly, 2008-10-14 17:24:55 |
|
